改訂版（五訂版）が刊行されていますが、旧版を用いている人が多いので、
問題番号や参照ページは旧版を優先しています。
改訂版は「新版」とし、括弧つきで記しています。

このホームページの記事の一部は改訂版(新版)に取り入れています。　改訂版を用いている人には重複と感じられるかもしれません。











///////////　 入試一般　 ////////////////////////////////////////





Q.　「エッセンス」の対象偏差値はどれぐらいですか？


A.　ありません！　ビックリしたかもしれませんね。
「エッセンス」の後、入試問題集に入ることになりますが、どこまで進むかが志望大学で変わってきます。
　「良問の風」まで終えれば、大半の国公立・私立大に合格できます。「風」は標準で頻出となっていますが、合否はそこで決まるのです。難問は解けなくても構わないのです。
　ただ、難関大を受ける人や物理を得点源にしたい人は「名問の森」まで進んでください。
＜重要＞と指定された問題をやっておくだけで大きな差が生じます。

　「大は小を兼ねる」という考えで「森」から入る人がいますが、とんでもない心得違いです。「分からないから、解き方だけ覚えておこう」となったら、物理の力は伸びません。
　自分の実力より少しだけ上のレベルに挑戦するのが最も効果的 なのです。

　「エッセンス」→「風」（→「森」）ですね。「エッセンス」の High の記述は飛ばし、練習問題でも難問**は飛ばしてよく、「風」を終えた後でもいいでしょう。






Q. 「エッセンス」は学校で習ったことについては要点が明解で分かりやすいのですが、　予習用に何かいい参考書はありませんか？


A.　物理は基本的には予習をする必要のない教科です。ただ、学校の授業が分かりにくかったり、自学自習をしいられたりする場合もあるでしょう。そんな時は「 物理 授業の実況中継」（語学春秋社）をお勧めします。
　「エッセンス」と違って 話し言葉 ですから、つながりが分かりやすく、物理の世界が「景色」として見えてきます。　そして、 重要事項 にスポットライトを当てているため、物理の骨格が浮かび上がっています。

　特に、原子分野は学校の授業が間に合わないまま受験に臨むという事態も起こりえます。「実況中継」は大いに役立ってくれます。

　「のっけから宣伝じゃん」と思うかもしれませんね。でも、「実況中継」は「エッセンス」とは別の味や工夫があって、負けていないと思っています。 その例が 物理の雑談 です。　楽しみながら学ぶ ことをモットーにしています。
　考えることを楽しむ と言ってもいいでしょう。　「授業」の中でも多くの質問を投げかけ、考えることを大切にしています。「 物理の考え方 」が自然に身についていきます。

　物理が得意だという人にも勧められる本です。 実際、何人かの先生から「ここは こう考えればいいんですね！」という声を頂いています。


Add　 改訂版が出ました！　上巻：2024年4月1日発行　下巻：近日刊　（上の紹介文も詳しくしました）

　

• 「はしがき」
　　　　　本の冒頭のコピーです

Q1.　物理を学ぶにあたっての 心掛けのようなものはありますか。


A.　「なぜ？」という疑問を大切にすることです。
　先ほど話した「実況中継」の序文に詳しく記していますので、引用してみます。　要点は 次の三角形です。

　

• 「実況中継」からの引用

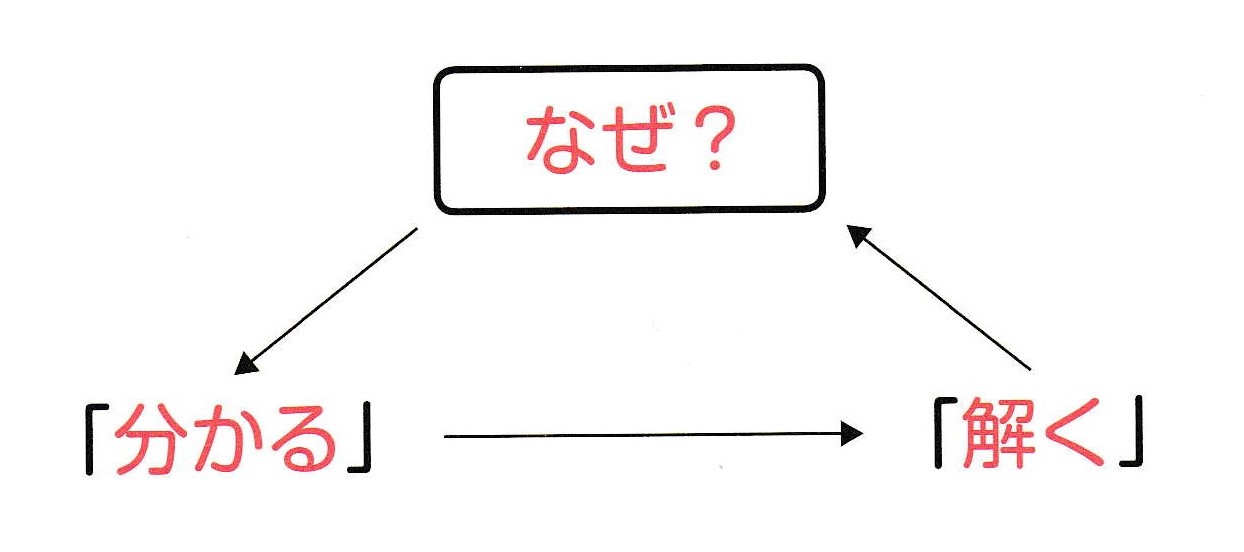
Q2.　「なぜ？」と考え始めると、よく分からないまま立ち止まってしまいます。


A.　すぐに解決できればいいのですが、たいていは「なぜ？」を抱え込んだまま進んでいくことになります。　本当には納得していないけど、問題には対処できるということは一杯あります。　それでいいのです。　そして、やがて「分かった！」が訪れるのです。

　誰もが成績が伸びることを願い、問題が解けるようにと思っています。　しかし、問題を解くのは　How の領域で、大切なことは確かですが、 Why にこそ物理の神髄があります。

　

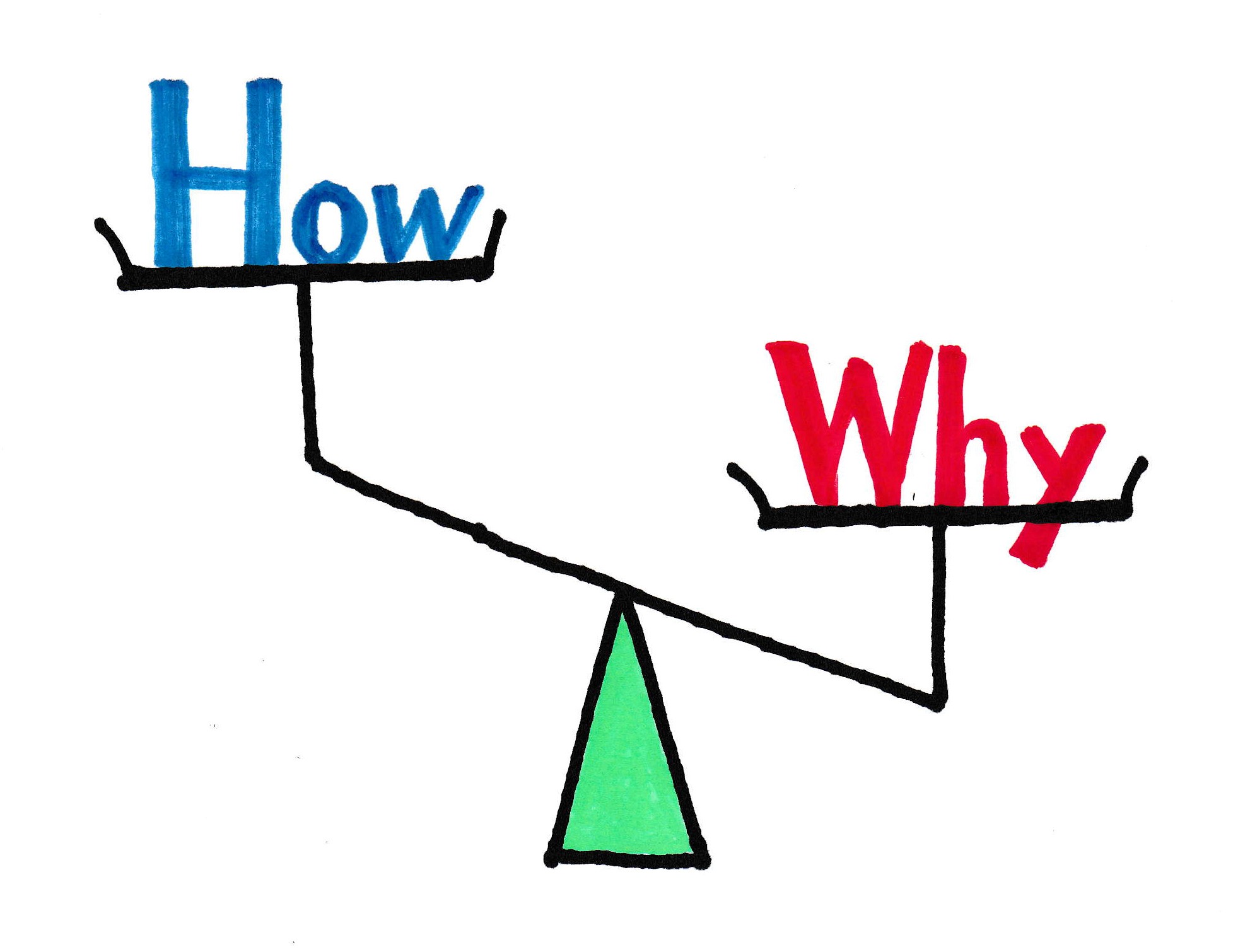
　「物理のエッセンス」は入試対策用ですから、解法の明示など How に力点を置いているのは言うまでもありません。ただ、そこに Why が散りばめられていることにやがて気づくはずです。


　物理と数学は近しいと言われていますが、数学は「いかにして解くか」に主な関心があって、両者の間には差異があります。　方程式の解を求めたり、関数の最大・最小を調べたり、幾何学で補助線をどう引くかなど、How が主体です。

　「なぜそうなるか」は自然科学の特徴であり、化学や生物や地学、どれもその一面を含んでいます。





Q3.　 物理が Why で数学が How なのは分かりました。　物理の方が優れているようにも聞こえますが・・・


A.　Why を強調するあまり、誤解を招きそうな表現になっています。　数学の How は洗練されたもので、幾何学、方程式、三角関数、微積分・・・など 創意・工夫がすばらしいと思います。

　さらに言えば、高校までの数学は How が主体ですが、大学からの数学は全く新たな評価になります。「自由な発想」とでも言ったらいいのでしょうか。
　たとえば、非ユークリッド幾何学がいい例です。　ある直線に対してある点を通る平行線は１本に限られるというのが常識で、ユークリッド幾何学を構成しています。　それに対して、平行線は１本もないとか、あるいは無数にあるとかという前提(公理)でも 矛盾のない体系ができあがります。
　荒唐無稽なものと思われていましたが、相対性理論が現れ、宇宙の構造を扱うとき、不可欠なものと分かったのです。　（ 相対性理論と言えば、ふつうは特殊相対性理論を意味します。　 ここでは 一般相対性理論です。）

　また、数学ではいろいろな「予想」がなされています。天才達が直観で気付いた「成立しそうな定理」と言ってもいいでしょう。　既知の事柄から証明したいのですが、意識としては Why の領域に入ります。研究の最前線は Why に満ちているのです。「既知」を超えて、新たな数学が必要なのかもしれません。
　高校段階でも 理解が深まるにつれて、Why という疑問が 各所に現れてくると思います。

///////////////////////////////////////////////////////////////////////////////////////////////////////

Q.　「・・・の大きさ」という表現によく出会います。その意味がもう一つよく分かりません。
　意味が一通りではないように思いますが・・・。 もちろん、物体の大きさは分かります。そうではなくて、「ある物理量の大きさ」のことです。

A.　確かに、二通りの意味で使われていますね。

　ベクトルの場合には「ベクトルの長さ」のことです。　たとえば、「力の大きさ」は力の強さを、「速度の大きさ」は速さを意味します。

　符号をもつ量の場合は「絶対値」のことですね。　たとえば、「仕事」とか「電荷」の場合がそうです。　念のためですが、仕事には正負がありますが、ベクトルではなくスカラー です。仕事を調べるとき、力の向きと移動の向きを確認するので、ベクトルと思われがちです。　電子の電荷は −e ですが、電荷の大きさは e です。
　座標軸の下での「ベクトルの成分」も符号をもちます。したがって、「加速度の ｘ 成分 a_x の大きさ」は絶対値 |a_x| のことです。

　いずれにしろ、「大きさ」は 正の値 です。　（正確には、０以上の値です。）





Q.　「単位 … 当たりの」という表現によく出会いますが、ピンときません。


A.　たとえば、「単位時間当たりの」は「１ｓ (秒) 当たりの」と読み替えてください。速さは 単位時間当たりに進む距離ですが、「１ｓ間に進む距離」の方が分かりやすいでしょう。「単位長さ当たりの」は「１ｍ 当たり」と、「単位体積当たり」は「１ｍ³ 当たり」と読み替えます。

　「単位 … 当たり」と書くのは、用いている単位系によらない表現だからです。　高校では国際単位系 ＳＩ を用い、長さの単位は ｍ ですが、ｃｍ を単位とする単位系もあり、そうなら、「１ｃｍ 当たり」と読み替えればいいのです。





Q.　「鉛直」と「垂直」は日常用語では同じ意味で使われることがあります。辞書でも確認しました。　物理では区別しているように思えますが・・・


A.　はい、区別しています。　「鉛直」は重力の方向で、「水平」と対にして用います。　鉛を糸でぶら下げれば、真っ直ぐな糸から「鉛直」が分かりますし、水が平らになる「水平」は文字通りですね。遠く離れた２か所が同じ高さになっているかどうかも、透明なホースに入れた水の両側の水面で分かります。　ピラミッドを造るとき、まず、岩盤を水平に削る必要があるのですが、溝を格子状に掘って水を満たして削ったという話です。
　一方、「垂直」は、ある直線や平面に直角をなす方向です。数学通りの用い方ですね。　「斜面に垂直に働く力を垂直抗力という」のように用います。

　入試問題でも、「鉛直」と書くべきところを「垂直」としている例がないわけではありませんが、不適切なのでまねしないでください。





Q.　加速度の単位 ｍ/s² の読み方は、教科書では「メートル毎秒毎秒」となっています。ところが、学校の先生は「メートル　パー　セカンド２乗」と言っています。 どちらでもいいんでしょうが、やはり、教科書には従うべきではないかと思うのですが・・・


A.　ウーン、私も先生と同じ呼び方をしているので・・・。　大学でもその方が多いのではないでしょうか。　教科書はある規約に基づいて表記していますが、両方の呼び方を書いたほうがいいのではないかと思っています。
　「メートル　パー　秒２乗」や「メートル　毎　秒２乗」などもあり、あまりこだわらなくてよいでしょう。
「秒２乗」は「平方秒」と言い替えできますし、発音も「メーター」や「セコンド」などいろいろです。

　ちなみに、英語では　meter per second squared　か　meter per square second　です。
　長年に渡って教科書が推奨（強制？）してきた「メートル毎秒毎秒」が浸透しないのは、英語に対応していないことに加え、「毎秒毎秒」という繰り返しがスマートさを欠くからか と思います。
　
　「 / 」を「パー」と読むか、「毎」と読むかは、他の単位でも一貫した方がよいでしょう。
　




Q.　数値計算の問題で、２ｓ や 15 ｍ/s や 120 ｍ などの数値が問題文に現れ、　桁数が１桁から３桁までバラバラです。　答えの有効数字は何桁にすればよいのでしょうか ？


A.　有効数字を考えるケースと、考えないケースがあります。

　見分け方は、2.0 や 12.30 のように、小数で末尾が ０ の数値があるかどうか です。あれば、有効数字に注意して答えます。
　質問の場合は、そのような数値がないので、有効数字は考えません。
　２ｓのように、１桁の整数が顔を出していることも指標になります。　与えられた数値は誤差のないもので、数学と同様の扱いですみます。
　もし、割り切れなければ、３桁目まで出しておけば十分です。４/３ なら 1.33 として答えます。　1.3 でもいいでしょう。　数値問題では分数にせず、小数で答えてください。 数学とは違う点です。

　有効数字は実験データを扱うときに必要なものです。誤差を含んだ数値だからです。 問題内容として実験がテーマであれば、考えることになります。 そのような場合も、入試問題では、末尾が ０ の数値を入れ、誤解が生じないようにしているのがふつうです。




Q.　有効数字を考えるときは、桁数の少ないものに合わせておけばいいんですね。


A.　それは掛け算と割り算の場合です。　足し算と引き算は、小数点以下の桁数が少ないものに合わせます。　詳しくは「エッセンス」（上）ｐ153（新版 p157） か、教科書で確認してください。











///////////　 力 学　 ////////////////////////////////////////





Q.　力のつり合い式ですが、たとえば、糸につるされているおもりの場合、「エッセンス」は 張力 T ＝ ｍ ｇ としています。でも、教科書は　T − ｍ ｇ ＝ ０ ですが ・・・


A.　教科書は力のつり合いの一般式として、 F₁ ＋ F₂ ＋・・・ ＝ ０ を掲げているので、それに従った表現にしています。　ただ、そうすると「上向きを正として」という宣言が必要です。 下向きを正にすれば、ｍｇ − T ＝ ０ ですから。　そんな宣言が不要なのが、（上向きの力）＝（下向きの力）の観点です。
　教科書は頭が固いと思います。「 T − ｍ ｇ ＝ ０　よって　T ＝ ｍ ｇ 」と書いてあるのを見ると、初めから分かることでは・・と言いたくなります。 教科書に書いてあることがベストとは限りません。

　力のモーメントのつり合いでも、一般式は　M₁ ＋ M₂ ＋・・・ ＝ ０　が数学的にきれいな表現ですが、 実際上は（反時計回りモーメント）＝（時計回りモーメント）が優ります。正負を機械的に決めていくより、モーメントがつり合って回転しないというイメージが描けます。　反時計回りが正であろうが、負であろうが、本来はどうでもよいのです。





Q.　「斜面上に物体を置き、斜面を傾けていくとき、物体が滑り出す角度 θ₀ を求めよ」という問題の答えを見ると、θ₀ で最大摩擦力として解いてあります。　しかし、最大摩擦なら、ギリギリ静止し、滑らないのではないでしょうか。


A.　確かに、ていねいな出題者なら「・・斜面を傾けていくと、θ₀ を超えたら滑り出した。θ₀ を求めよ」とします。　が、質問のような表現もなされます。分かりやすいことに加えて、現実には、滑り出すのを見てしか、最大摩擦を超えたと判断できないからです。　そのときの角度は「θ₀ ＋ 無限小」ですが、無限小は無視できます。
　数学と違って現実を相手にする物理では、ギリギリの境目にはあまりこだわっていません。　摩擦に限らず、一般にそうです。

　とは言え、「最大摩擦まで静止」が原則 であることに変わりはありません。それを踏まえた解答を心掛けてください。　もしも、「滑り出すための角度 θ に対する条件を求めよ」であれば、「 θ ＞θ₀ 」と答えます。（実際には、tan θ₀ ＝ μ (静止摩擦係数) なので、tan θ ＞ μ ）





Q.　静止摩擦力の向きの決め方に迷うことがあります。


A.　まずは、「もしも摩擦がなかったら、どちらへ動くのか」と考え、その逆向きと判断します （エッセンス（上）p22）。それでも右なのか左なのか、分からないケースはあります。　そのときは「右向き F 」と仮定します。つり合い式を解いた結果、F が正なら、それで OK 　F が負なら、左向きと判断します。大きさは｜F｜で、計算のし直しは不要です。

　はじめに「左向き F 」でもいいですが、仮定して進み、答えの符号で判断する のは、いろいろなケースで出会います。　衝突問題での速度の仮定はその典型ですね。座標軸があれば、正の向きに仮定するのが分かりやすいでしょう。





Q.　力学を習い始めた高校１年生です。いろいろな力を習っています。　重力や張力、垂直抗力、摩擦力は分かりますが、浮力がよく分かりません。　浮力Ｆが働くことは体験からも明らかですが、Ｆ ＝ ρＶｇ となる理由が分からないのです。
　　　　　　　　　　　　　　　　　　　（ ρ：液体の密度　Ｖ：液面下の体積　ｇ：重力加速度）


A.　浮力の理解は難しいので、後回しにしてください。　ずっと先になって、気体の圧力を理解してからがよいと思います。　今、浮力が理解できなくても、力学を学ぶ上で困ることはありません。先につながらない袋小路みたいな内容です。

　浮力は複雑な力で、本当は教科書のもっと後ろに回したいのですが、適当な場所がないので強引に入れられています。

　「重心」と「剛体のつり合い」も袋小路的です。　そして、ある程度 力学の実力がついてから学ぶ方がいいテーマです。
　大通りで続いていくのは、つまり、大事なのは 「力のつり合い」と「運動方程式」 です。





Q.　「エッセンス」には「液体の圧力は、深さが同じなら（同じ水平面上なら）同じである。また、液体中での面の方向によらないことが知られている。」とあります ((上)ｐ25)。　前半は分かりますが、後半の「面の方向」がイメージできず、意味が取れません。


A.　液体中のある深さに小さな板（平面板）を置いた場合、板にかかる圧力は 板の向きによらないという意味です。水平でも、傾けても 圧力は同じです。　単位〔Pa〕＝〔N/m²〕からも分かるように 圧力は 単位面積当たりの力 であり、面を想定してのものです。「小さな板」としたのは深さを同じにするためです。
　板がなくても、液体中の ある平面を考えたとき、その面（液体自身の面）にかかる圧力は、深さが同じなら面の向きにはよりません。平面をはさんで２つの液体が接触していると考えての話です。

　結局のところ、面の方向によらないので、「ある深さでの圧力」や「点Ａでの圧力」のような表現ができます。面を指定しないどころか、面の存在さえ意識しない表現です。





Q.　問題集で「垂直抗力を求めよ」となっているのに、答えを見ると、垂直抗力の大きさだけが書いてあり、向きが記されていません。　力の向きは答えなくていいのですか。


A.　出題者は力の向きを尋ねたい場合には、そのように指示します。
　指示がない場合は「大きさ」だけと思ってください。　力の向きが自明に近い場合にそうなることが多く、垂直抗力や張力などが該当します。もちろん、力の向きも答えていいです。
　教科書や模試では「…力の大きさ」とていねいに書いていますが、入試では必ずしもそうではありません。

　ベクトルでは、大きさと向きを答える というのは、原則としては 正しいです。
　力学では、力、変位、速度、加速度、運動量、力積 がベクトルですね。




Q.　力を矢印で図示するときの作用点ですが、教科書では丸で明示しています。　一方、「エッセンス」をはじめ、多くの参考書は丸を付けていません。どちらでもいいのでしょうか。


A.　どちらでもいいです。　大学の教科書は、つまり物理学としては矢印だけです。
　高校の教科書が丸を付けるのは「力の三要素」の一つとして、作用点を意識してほしいという教育的な配慮です。　たとえば、作用・反作用ではどちらの物体が受けている力かが分かりやすくなります。
　ただ、いつまでも丸を付け続ける必要はないと思います。　教科書は一度ルールを定めると、一貫させる責任が生じてしまい、自縄自縛の感があります。

　三要素と言っても、同等のウエイトではなく、「大きさ」と「向き」こそが大切で、まさに数学のベクトルです。ベクトルの始点に丸は付けません。　そして、作用点が重要になるのは、力のモーメントを扱うときだけです。

Q.　「軽い糸」は「質量が無視できる糸」と同じ意味でしょうか？　また、問題によっては「糸」としか書いてない場合があります。どう対処すればいいのでしょうか。


A.　糸に限らず、「軽い」は質量を無視してよいことを意味します。　何も断りがない場合も、糸の質量は無視してください。　「ひも」もそうです。　略式の問題ではよく見かけます。　質量が無視できないのなら「綱」や「ロープ」にしますし、何より、質量が明示されるので 迷うことはないはずです。
　また、「ばね」も同様です。　「軽いばね」と書いてなくても、質量を無視してください。　結局、糸 と ばね の質量は無視 ということです。

　このホームページの記事でも、断らなければ 糸とばねについては そう判断してください。

　「軽い」と似た例に、「小さな」があり、「大きさを無視してよい」ことを表します。　「小物体」や「小球」も同じです。　「質点」も同じで、質量をもつが大きさは無視できる物体です。






Q.　運動方程式を扱うとき、座標軸を定めたら、ベクトルに対しては、座標軸の正の向きを正にする のですか？

A.　そうです。　ｘ軸を定めれば、速度・加速度・力すべてが ＋ｘ 方向が正になります。
　２次元や３次元の場合には、ベクトルの成分に対してそうします。

　運動方程式に限らず、座標軸があれば、ベクトルの正負はそれに従ってください。
　たとえば、衝突問題で座標軸が登場すれば、速度・運動量・力・力積の正の向きが指示されています。

　問題文で指示があれば、それに従うのは言うまでもありません。上記に反する指示を出す出題者はいないと思いたいのですが・・・





Q.　運動方程式を扱うときには、力の図示が大切なことはよく分かっています。　ただ、問題集や参考書で、摩擦のある面上を滑る直方体のときなど、「垂直抗力の作用点がおかしい」と思うことがあります。　作用点はいい加減でもいいのでしょうか。


A.　作用点が大切になるのは、力のモーメントを扱うとき です。　剛体のつり合いや、てこの原理が代表例ですね。　力のモーメントを扱うときとは、「回転」が問題になるときと言いかえてもいいです。　傾くのも回転の一種です。

　運動方程式のときは適当でよいのです。　力の矢印が重なり合わないように見やすくするため、適当な位置にしていることはよくあります。　力の分解が必要になることが多いのですが、その矢印が交差しないようにしています。　力のつり合いでも同様です。
　また、摩擦があり、いくつもの力が働くと、垂直抗力の作用点がどこにあるか即断できないこともあります。　でも、 運動方程式 や 力のつり合い なら気にしなくていい のです。

　教科書はクレームを恐れ、すべての場合で作用点に気を使っていますが、「正しさ」に捕われ過ぎと思います。　結局、作用点に気を使うかどうかは、「目的に応じて 臨機応変に」ということですね。







Q1.　力の図示に限らないと思いますが、図を描くときには、扱う内容に関係しないことは気にしなくていいということですね。


A.　 現象に関わる重要な要素を見極めることが何より大切 です。　図は、誇張してよいので本質を浮き立たせること、一方、不要な詳細は思い切ってカットすることです。

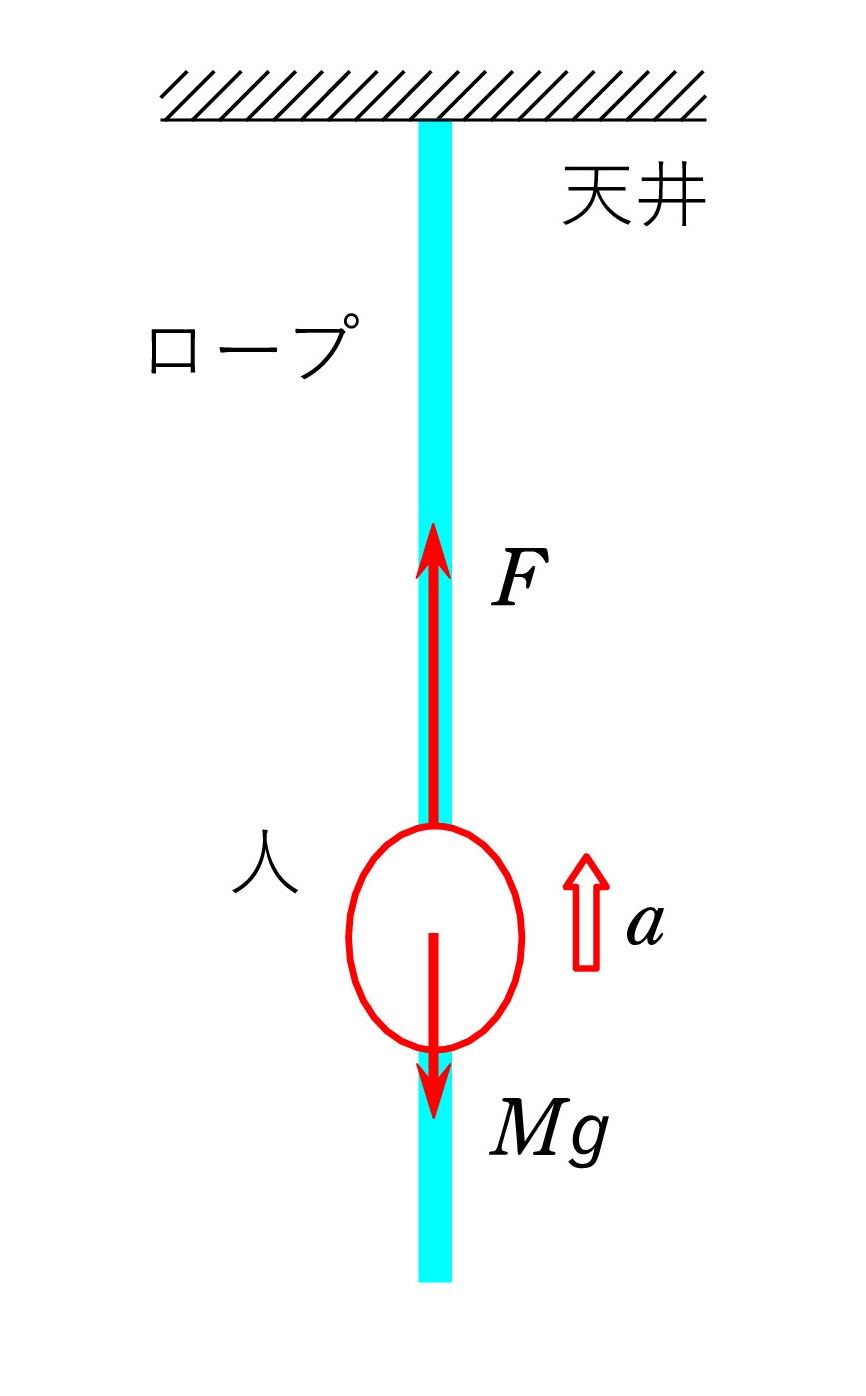　たとえば、天井から垂らされた軽いロープを、質量Ｍの人が登っていくケースとします。　　図示は人を丸か四角で表し、下向きの重力 Ｍｇ と上向きの力Ｆを描けば十分。　上向きの加速度を a とすると、運動方程式は　Ｍa ＝ Ｆ−Ｍｇ　ですね。


　なお、Ｆは張力です。　人はロープに下向きの力を加え、その反作用Ｆを上向きに受けるからというのが、ていねいな説明です。でも、人も物体と思えば・・・ロープからの力は張力に他ならないはずです。 ロープが人を吊り下げている と考えてもいいのです。

　問題文で「人はロープに下向きに力Ｆを加え・・・」となっていても迷わないように。　　運動方程式での力は「注目物体が受けている力」です。　そして、２つの物体間で働く力は、作用・反作用の法則 に従います。　作用・反作用は 物体が静止しているとき と思っている人がいますが、誤解です。　運動中の物体でも作用・反作用の法則は成り立ちます。

　また、Ｆは合力です。　両手・両足を使って登っていても、合力がＦであれば構いません。




Q2.　人間が関わると、実感できる「与えている力」にとらわれてしまいます。　「受けている力」に目を向ければ、人間も単なる物体ということですね。　難しく考え過ぎていました。
　ところで、「上向きの加速度を a とすると」とは、上向きを正の向きにするということですね。　加速度以外のベクトル量も含めてということでしょうか。


A.　そうです。　「上向きに座標軸を設定する」と言えば明確になりますが、仰々しいので、サラッと表現しています。　運動方程式の右辺に現れる力の正負もそれに従っています。　右辺は合力で、ベクトルである力の和 ですから、ていねいに書けば、 Ｆ＋(−Ｍｇ) です。




Q3.　力の矢印の横には力の大きさを書くのですね。　重力の矢印に −Ｍｇと書いてはいけないのでしょうか。


A.　普通は大きさを書きます。　正の向きをどうするかによらない表現が優ります。　図示の段階では、現実がどうなのかが誰にも分かるようにしたいのです。　正負の意識はありません。　正の向きを決めた後で、＋Ｍｇ なのか、−Ｍｇ なのかを読み取ります。　力 以外のベクトル量も同じです。
　正の向きの取り方は自由ですが、初めの運動方向にとるのが分かりやすいでしょう。　　座標軸があればそれに従います。

　ただ、ベクトルの向きが明確でない場合には、正の向きを先に定め、矢印は正の向きにします。　運動方程式では、加速度 a が未知のことが多く、それに該当します。　a は符号付きで、計算の結果、a＜０ となれば、負の向きで 大きさは｜a｜と判断できます。　力のつり合いやモーメントのつり合いで、静止摩擦力の向きが不明というケースがありますが、同様に対処します。
　未知のベクトルは正の向きにして図示し、符号付きで扱う のがセオリーです。　式にするときも正と思って扱います。

　ロープと人の場合も、Ｆが小さければ、人は下へズルズルと落ちていくでしょうが、運動方程式はそれも含んで成立しています。　 Ｆ＜Ｍｇ で、a＜０ のケースです。




Q4.　静止も含んでいますね。　 Ｆ＝Ｍｇ のときです。　運動方程式は「静止」での力のつり合いも含んでいると習いました。


A.　 その通りです。　ただし、Ｆ＝Ｍｇ のときは、静止以外の可能性もありますよ。


　　　　　・・・・・・・・？・・・？・・・？・・・？・・・？・・・・・・・・





Q5.　今、気が付きました！　等速度運動ですね。　上に等速で上がっていく場合がありました。
　静止なら力がつり合っていますが、等速度でも力がつり合っていました。


A.　 「力のつり合い ⇔ 等速度」は重要です。　両矢印は必要十分であることを示しています。　等速度は静止も含みます。　また、等速度は向きまで含めてなので、等速直線運動と同じです。

　見落とされがちですが、Ｆ＝Ｍｇ の場合、人が下へ等速で降りていく可能性もあります。









Q.　仕事とエネルギーは同じものと考えていいですか。　単位ジュール〔 J 〕も同じですし。


A.　同類ですが、違いがあります。エネルギーの方が価値が高いのです。あるいは格が上と言ってもいいでしょう。　また、エネルギーは物体の状態で決まり、蓄えることができます が、仕事は蓄えるものではありません。仕事はどれだけのエネルギーが出入りしたかを示しているだけです。

　たとえば、縮んでいるばねは弾性力によって仕事をすることができますが、エネルギーを蓄えていると見たいのです。それが弾性エネルギー（弾性力による位置エネルギー）です。力のする仕事を位置エネルギーに格上げした のです。弾性エネルギーを用いることによって、弾性力の仕事はもはや考える対象ではなくなっています。「エッセンス」(上)ｐ55 Q＆A も参考にしてください。






Q.　力学の問題は解法がいろいろあって、迷います。たとえば、斜面を滑る物体の運動だと、運動方程式でも、仕事でも、エネルギー保存でも解けるということが起こります。力積だって利用できそうで、目が回ります。　何か方針はないんですか？


A.　運動方程式で攻めるか、保存則で攻めるかの二大戦略 です。
　時間に関する話は運動方程式ですね。力を確認し、加速度を求め、等加速度運動の公式を用いて解決していきます。時々刻々の運動の詳細が分かります。
　時間が絡まなかったり、力が変わっていくときには保存則です。曲線運動もそうですが、運動方程式で扱いきれない状況でも活躍してくれます。

　以下は、保存則についての注意点です。
　まず、エネルギー保存則。すべての現象において、エネルギーの移り変わりを考えることは大切です。
　次に、運動量保存則ですね。運動量保存は衝突や分裂のケースでは必須です。ベクトルの保存則なので、ある方向だけで成立することもあって、慣れが必要ですね。

　２つの保存則は独立です。つまり、一方だけが用いられることもあれば、両立することもあります。エネルギー保存は関連するすべてのエネルギーを考えたかどうか、運動量保存は物体系に外力が働いていないかどうかで、見るべきポイントがまるで違います。


　「仕事 ＝ 運動エネルギーの変化」や「力積 ＝ 運動量の変化」という定理は指示がない限り、用いないという姿勢でいいでしょう。　仕事や力積は思い浮かべなくていいということですね。






Q.　摩擦のある平面を滑る場合、動摩擦力の仕事を考えよと教わりましたが…
　運動方程式を用いない場合の話です。


A.　エネルギーである 摩擦熱 を考えれば済みます。　動摩擦力と滑った距離の積 で求まります。　動摩擦力の仕事は 負ですが、摩擦熱は 正で扱いやすい点が有利です。
　たとえば、斜面上、ある初速で滑り降りた物体が止まったのなら、失った運動エネルギーと位置エネルギーの和が 摩擦熱 に等しいと式を立てます。

　このように、 エネルギー保存則では （失った分）＝（現れた分）という見方 をよくします。
　斜面を登って行って止まったのなら、（初めの運動エネルギー）＝（位置エネルギーの増加分）＋（摩擦熱） ですね。　細かいことを言うと、ここでの摩擦熱は 滑る際に発生する音のエネルギーなども含んでいます（摩擦熱が大半です)。

　




Q.　加速度運動している電車内の物体には慣性力が働くはずですよね ？


A.　それはちょっと違います。誰が物体の運動を見るかが問題です。　車内の人が見れば、慣性力が働きます。車外で静止している人にとっては慣性力などありえない力です。ただ、車内で見て何が起こるかが問題となることが多いので、慣性力が登場しているのです。

　慣性力を用いるときは、必ず（電車内の）観測者を意識してください。　その人が見て物体が静止していれば、力のつり合い、動いていれば運動方程式を適用します。そこでの加速度はその人が見たものだから、相対加速度ですね。電車に対する運動（相対運動）が決まるのです。
　教科書の記述が力のつり合いになっているため、力のつり合いしか扱えないという誤解が多いので、この際、改めておいてください。






Q.　遠心力は円運動での慣性力で、いわば見かけの力ですね。円運動では遠心力を用いるべきかどうか、迷います。


A.　自由に解いていいのなら、用いるべきです。
　等速円運動なら、遠心力のおかげで、任意の方向で力のつり合いが成立します。　計算しやすい方向が選べます。
　遠心力を用いないと、解き方が制限されます。つまり、円の半径方向で運動方程式を用い、円を含む平面に垂直な方向で、力のつり合い式を立てるという限定です。

　等速でない円運動でも、遠心力は有効です。　力のつり合いは半径方向に限られますが、運動方程式より扱いやすいでしょう。　もっと大事なのは 現象のイメージがつかみやすい ことです。　たとえば、糸に結ばれた小球が 鉛直面内で円運動しているとき、最高点を通過できるためには 外向き(上向き)に働く遠心力が 重力を上回ればいい、と即断できます。　その差分だけの張力が生じています。
　現実の力である張力より、見かけの力である遠心力を優先させていることに注意してください。そのおかげでずっと分かりやすい解釈ができているのです。

　なお、遠心力は mv^２/ｒ または ｍｒω^２ ですが、 ｍ・ｖ^２/ｒ と ｍ・ｒω^２ と覚えてください。　慣性力なので、ｍ ×（加速度）の形をしていて、加速度は向心加速度です。　　遠心力の公式を知っていれば、向心加速度の方は覚える必要がなくなっています。






Q.　等速でない円運動での遠心力は、 mv^２/ｒ だけが用いられていると思います。
　ｍｒω^２ がダメな理由は何でしょうか。


A.　ダメというわけではありませんが、角速度ω が一定でなく、時間とともに変化し、扱いにくいからです。 速さｖも変化しますが、こちらは力学的エネルギー保存則にも登場する大切な物理量です。　鉛直面内の円運動だと、ｖを用いて、遠心力による半径方向での力のつり合い と エネルギー保存則 を連立 させることができます。

　ｖ＝ｒω 　の関係は常に成り立つので、ω を未知数にすることも可能ですが、速さｖを知りたいケースが殆どです。
　





Q.　反発係数（はね返り係数）e の式の表記ですが、教科書では　e ＝ −（衝突後の速度差）/（前の速度差）と分数形になっています。 一方、「エッセンス」は （衝突後の速度差）＝ −e ×（前の速度差） です。 同値とはいえ、なぜ、あえて変えるのですか。
　

A.　分数形より覚えやすく、「後」と「前」の順序のミスが減ります。　何より、衝突問題で運動量保存則との連立方程式を解くとき計算しやすいからです。 ２物体の衝突後の速度 ｖ₁、ｖ₂ が未知数になるのがふつうですが、まず、保存則を （後）=（前） の形で書いておきます。
　　　　　　　　　 ｍ_１ｖ_１ ＋ ｍ₂ｖ₂ ＝（衝突前の運動量の和）　　・・・�@　
　次に、e の式　　　　　　ｖ₁−ｖ₂ ＝ −e ×（衝突前の速度差）　　・・・�A
　未知数が左辺にそろっていることに注意してください。 あとは ｖ₁ が知りたければ、
�@ ＋ ｍ₂ × �A　と辺々で ｖ₂ を消去します。 　ｖ₂ が知りたいのなら、 �@ − ｍ₁ × �A として。
　�@、�Aを上下に並べれば、慣れると暗算でもできます。
右辺だけていねいに計算し、（ ｍ₁ ＋ ｍ₂ ）で割ればよいのです。

　辺々の計算は代入法よりずっと早くできます。　言い遅れましたが、「速さ」ではなく「速度」であることに注意してください。






Q.　直線上で衝突が起こり、弾性衝突でないときは、力学的エネルギーの一部が失われるというのは分かります。　衝突では音が発生しますから。　ただ、失われたエネルギーの大半が熱になるというのが分かりません。　衝突の際、２物体が擦（こす）れ合うということでしょうか、正面衝突なのに・・・？


A.　弾性衝突は 反発係数 e ＝１ のケースですね。　 e ＜ １ のケースでは 力学的エネルギーの一部が失われます。　力学的エネルギーは運動エネルギーと位置エネルギーをまとめての用語ですが、衝突で失われるのは運動エネルギーです。　確かに 大半が熱になるのですが、ちょっとメカニズムが違います。

　衝突した物体のそれぞれは、衝突時の衝撃で圧縮され、離れた後は伸び縮みしながら振動して動きます。　そして、物体内部の摩擦で振動が収まっていく過程で熱に変わります。目には見えない振動で、短い時間の出来事です。ブルブル振動するといったイメージです。
　各物体の重心の速度はそれぞれ一定で、それが衝突で扱っている速度です。
　物体によっては、衝突時の変形（凹み）が戻ることなく、そのまま熱になることもあります。
　






Q.　重力は 万有引力と 地球の自転による遠心力 の合力 だと習いました。　ところが、テレビの科学番組を見ていると、万有引力そのものの意味で使われていると思うことがあります。


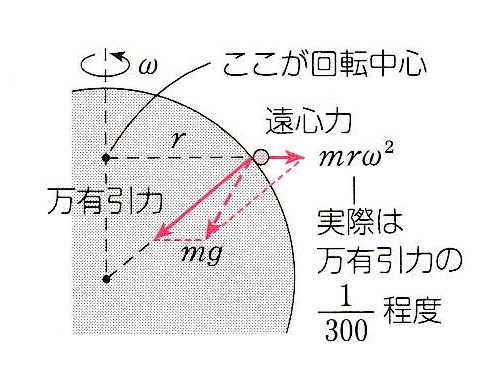A.　高校物理では合力と思ってください。　地球上での重力 mg を問題にしています。　mg こそ 鉛直( と 水平) を決める大切なものです。　日常現象は mg の支配下で起こります。　地面が水平面と見なせる場合です。
　一方、万有引力は ＧＭｍ/Ｒ² と表されます。　地球の全質量は中心に集まっているとしてよく、万有引力の法則を用いて出された式です。
　　　（Ｇ：万有引力定数、Ｍ：地球質量、Ｒ：地球半径）

　図のように、自転による遠心力のために、mg は万有引力以下になっています。
　極(北極と南極)では遠心力がなく mg は最大で、万有引力に等しく、赤道では遠心力が最大で、万有引力と逆向きになるため、mg は最小となっています。
　重力加速度ｇは 極で最大、赤道で最小 と言ってもいいです。
　以上、ていねいには「地表での重力加速度」です。　高度が高くなれば、ｇは減少していきます。

　遠心力は万有引力に比べてかなり小さいので、現実的には、 mg ≒ 万有引力 となっています。　上の図では 遠心力が誇張されていることも意識してください。
　入試問題では「自転の影響を無視する」ことが多く、その場合「 mg ＝ 万有引力 」です。


　さて、大学になると、万有引力のことを重力と言うことが むしろ普通になります。紛らわしいですが・・・。　科学番組や一般の科学の本も同様です。
　その場合、地球という特別な天体の話ではなく、宇宙一般に対して用いられています。　「木星の重力に引かれて 彗星が衝突するのが観測されたことがある」とか。

　あるいは、自然界での根源的な力として、重力は 電磁気力と共に用いられています。
　電磁気力は 静電気力など電磁気に関わる力の総称です。　糸の張力、ばねの弾性力、面の垂直抗力や摩擦力などは、突き詰めれば、分子・原子間での電磁気力に他なりません。
　私達が目にする世界は 重力と電磁気力で構成されているのです。

///////////　 波 動　 ////////////////////////////////////////





Q.　波は 横波と縦波に分けられるのですか。


A.　大学入試で「波は横波と□波に分けられる」という穴埋め問題が出たぐらいで、大学の先生でさえ誤解している人がいますが、どちらでもない波もあります。　身近な水面波がそうで、媒質である水は一点に注目していると、鉛直面内で円運動に近い運動をしています。

　ただ、問題として出会ったときは、断りがなければ、水面波は横波とみなして考えてください。　「音波は□波であり、水面波は□波である」という出題さえありました。解答用紙はそれぞれ１文字分の空欄でした。





Q.　波動分野に入って、いきなり波の式に出会い、わけが分からず、立ち止まってしまいました。


A.　波の式が分からなくても今後の波動の学習には差し障りはありませんから、安心してください。　波の式は、昔、教科書から外されたこともあったぐらいで、大して重要なことではありません。
　分からないことに出会ったら、取り合えず、受け流して先に進んでください。いずれ分かる時が来ます（大学に入ってからかもしれません）。　公式などでも使ってみているうちに分かるということはよくあります。
　分からない点をメモしておくことは大切です。「？」だけでもいいので、記しを。

　理解とは、建物を建てるように、基本から積み上げていくものとよく言われますが、実際には、塗り絵を塗るように分かったところから塗り広げていくという面もあります。
　さらには、より深い理解を目指す…というふうに、多面的で重層的なものです。







Q.　「時刻」と「時間」は区別して使った方がいいのでしょうか。


A.　２つの時刻の差が時間なので、区別を意識してください。　時刻は用いる時計によって変わりますが、ある現象が継続した時間に変わりはありません。
　座標と距離の違いと似ています。　座標軸の原点の取り方で、各点の座標は コロコロ 値を変えますが、２点間の距離に変わりはありません。

　時刻のことを広い意味で時間と呼ぶこともあります。 グラフの横軸ｔは 時間軸と呼ばれますが、目盛りが表しているのは時刻ｔですね（ｔ＜０もありえます）。　ｖ−ｔグラフを 速度―時間グラフと呼ぶのもこの例です。

　とくに波動分野では、時刻と時間の違いを明確にする必要が生じることがあります。
　波源が移動しながらある時間だけ波を発生すると、人がそれを受け取る時間が異なるのです。　初めの波を受け取った時刻と、終わりの波を受け取る時刻を調べて時間を決めることになります。






Q.　定常波って、干渉の一種なんですか？


A.　そうです。　腹が強め合い、節が弱め合いに対応 しています。
　水面波の干渉で、２つの波源を結ぶ線分上に注目してください。波源から出て逆向きに進む波が干渉しています。まさに定常波ができているのです。　水面全体では、強め合いの線と弱め合いの線が双曲線になって、交互に現れていますね。

　「水面には何本の強め合いの双曲線が現れているか」という問いかけには、定常波の腹の数を調べればよいことになります。　まず、波源間の中点に着目します。　２つの波源が同位相なら中点は腹、逆位相なら節です。　次に、腹と腹（節と節）の間隔が半波長 λ/２ であることを利用すればよい のです。






Q.　ドップラー効果のところで、「波長 λ は観測者によらない」とのことですが、よく分かりません。


A.　波長 λ は、静止している人が測っても、動いている人が測っても 同じということです。　波長 λ は波形での山と山の間隔でした。波形はある瞬間のものです。
　たとえば、海の波をイメージしてください。岸に立っている人が写真を撮って λ を測るとします。　一方、ヘリコプターで飛んでいる人が写真を撮って測るとします。　写った波の様子は同じでしょ。山と山の間隔 λ も同じですね。
　念のためですが、波の速さと振動数は観測者によって異なります。







Q.　ドップラー効果では、波源が動いても波が伝わる速さに変わりはない ということが　キーポイントと思います。　その理由も「エッセンス」（上）ｐ117 (新版 p119) の『ちょっと一言』で分かった気がします。
音波が伝わるときは、地面に対しての音速 Ｖ が一定という理解でよいでしょうか ？


A.　それで ＯＫ です。　もう少していねいに言うと、静止している大気（空気）に対しての音速 Ｖ が一定です。

　どちらでもいいようなものですが、風が吹くと、つまり空気が移動すると違いが出ます。　風速を ｗ とすると、風下に伝わる音波は地面に対しては Ｖ＋ｗ で伝わります。空気自体が１秒間に ｗ だけ移動するからです。　一方、風上には、音波は Ｖ−ｗ で伝わります。
　振動数の公式 ｆ ＝ ｆ₀（Ｖ−ｕ）/（Ｖ−ｖ） では、分母と分子にある２つの Ｖ を、　Ｖ＋ｗ に置き換えればすみます（あるいは Ｖ−ｗ に）。　（ u ：人の速度、　v ：音源の速度 ）

　言うまでもないことですが、音波に限らず波一般に成り立つ話です。　空気は「波が伝わる媒質」に、音速は「波の速さ」に置き換えて理解してください。　水が流れているときの水面波の出題もあります。
　なお、断りがなくても、ｕ、ｖ、ｗ は Ｖ より小さいと思ってください。







Q.　音波は空気中だけでなく、水中でも伝わりますよね。なのに、音波で「水の屈折率」という言い方をしたら、おかしいと言われました。何が悪いのですか？


A.　音波を含めて波一般の話と光（光波）の話が混線しています。 屈折率は２つの媒質によって決まるのです。媒質�Tから入射して、�Uで屈折する場合には、�Tに対する�Uの屈折率（ていねいには相対屈折率）といい、ｎ₁₂ のように表します。

　ただ、光については、�Tを真空と限定した場合の屈折率を扱い、絶対屈折率と呼びます。光なら「水の屈折率」は問題ありません。水の絶対屈折率のことです。ところが、音波だと、空気から水に入るのか、ガラスから水に入るのか相手を決めないと屈折率は語れません。

　屈折率ｎ₁₂ は２つの媒質中での波の速さの比に等しい――公式 ｎ₁₂＝ｖ₁/ｖ₂ ですね。この式も２つの媒質で決まると言ってますよ。

　ついでながら、「 n sinθ ＝ 一定 」という定理がありますが、これも光だけについてのもので、n は絶対屈折率です。 (エッセンス（上）p126(新版 p128))






Q1.　 音波の干渉はふつうの波と同じと考えてよいのでしょうか？


A.　音波は縦波ですが、直線上を伝わる場合は横波表示と呼ばれる方法で波形が描け、横波と同じように扱えます。　気柱の共鳴ではまさにそれが役立ちました。
　ところが、平面上を伝わる場合や空間内を伝わる場合には、縦波の本来の性質である、疎密波としての扱いが必要になります。　密や疎が伝わるという観点なら、ふつうの波と変わりありません。
　今ちょうど新課程に向けて「エッセンス」を改訂中で、音波の扱いについて取り上げていますので、改訂原稿を掲載します。　 （文中に現れる問題52 や p132も参考に付けています。）

• 「音波の干渉」
　(新版はp136に掲載済み)

【ひとこと】

　上記の２つのスピーカーの間に生じる定常波について 一言加えておきます。　面倒だと思う人は読み飛ばして構いません。　どちらかと言えば、先生方へのコメントです。

　定常波の波形を変位の横波表示で描くと、中点 M は節になります。　密度変化を縦軸にして描くと、腹になります。　「腹では大きな音になる」という主張は「 密度変化に注目すれば」という前提が必要です。
　２つの音源（スピーカー）は変位では逆位相、疎密では同位相です。

　２つの音源による音波の干渉問題で、変位か疎密かを断ることなく「同位相」となっているときは、「疎密で同位相」と解釈すると、出題者の意向に合うと思います。　２次元の干渉では まず間違いなくそうです。


　※　さらに詳しい話は「探究の旅に出よう」の中の「音波の干渉の考え方を確立したい」にあります。





Q2.　 ある入試問題についての質問です。　ｘ軸上の２点ＡとＢに音源を置き、ＡＢ間に生じる定常波を波の式によって調べます。　変位で考えていて、２つの音源は同位相となっています。　先ほどの話からすると、「逆位相」の誤りではないでしょうか？


A.　同位相の音源もあり得ます。　ｘ軸に垂直な板の振動を考えてください。２枚の板が同じ振動をしている場合です。　左の板Ａの右面から出る音波と 右の板Ｂの左面から出る音波は 変位で同位相です。　中点Ｍは（変位で描いた）定常波の腹になります。

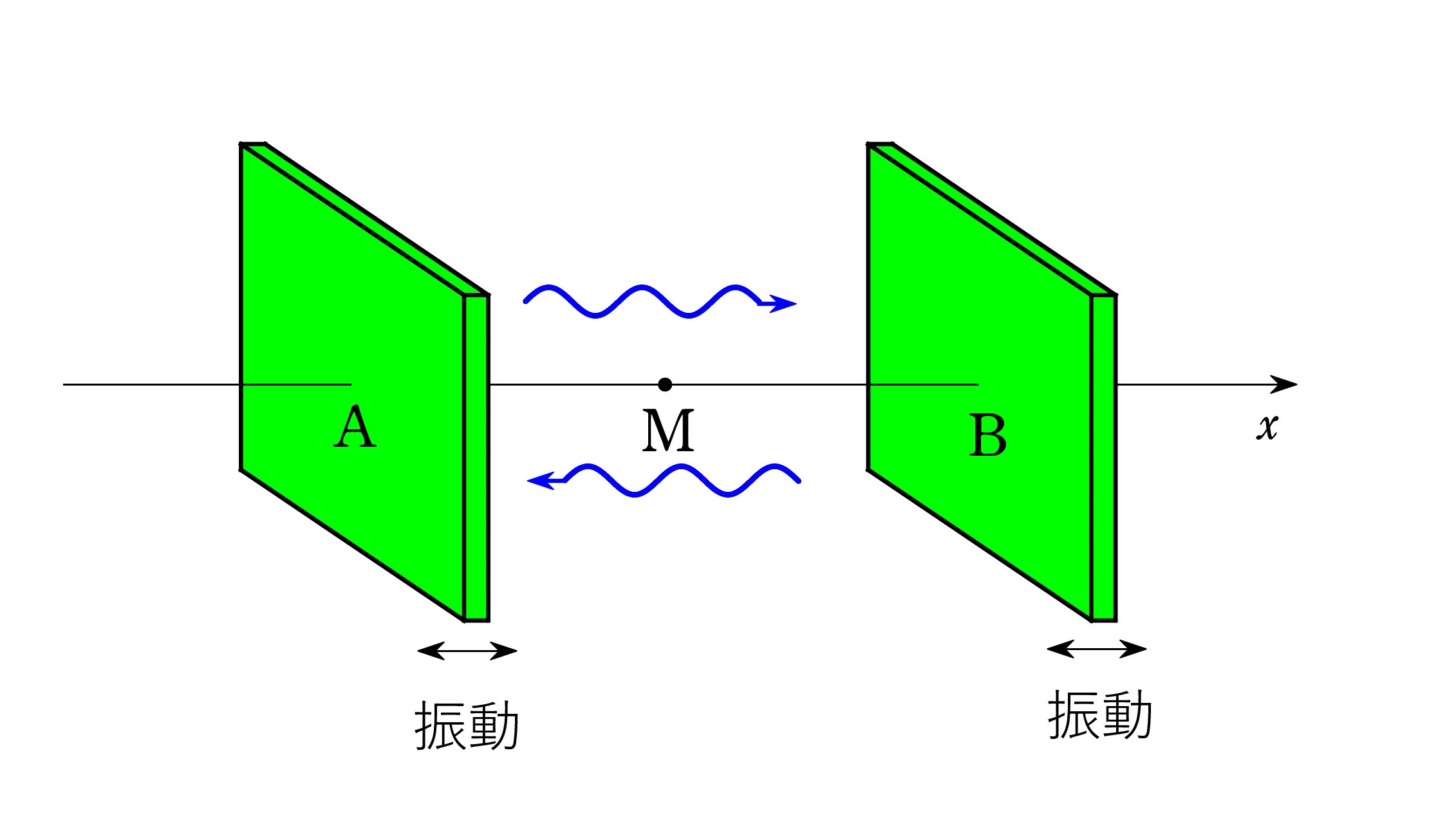
　疎密で考えると、板が右に動くと、右側の空気を圧縮して密を生じ、板の左側には疎を生じます。　Ａが密を発生させるとき、Ｂは疎を発生させるので、逆位相です。　Ｍでは 密と疎が出合うので、音が小さくなっています。　

　２枚の板が逆向きに振動すれば、変位で逆位相になります。

　先ほどは（同じ電気信号で作動する）スピーカーを向き合わせたので、変位は逆位相となりました。　２枚の板の逆向き振動と同じです。
　スピーカーでも、逆位相の電気信号で作動させれば、変位で同位相にできます。

　結局、２つの音源の位相の関係はどうにでもなるということですね。

　










///////////　 熱　 ////////////////////////////////////////





Q1.　単原子分子気体の定圧変化での熱量の計算ですが、「エッセンス」や「良問の風」では　Q ＝ n C_P �儺 と C_P＝5/2・R とから求めています。
　学校では、気体がした仕事を P�儼 で求め、内部エネルギー U の変化を U＝3/2・nRT で調べ、熱力学第１法則を用いて求めています。この前受けた模試でもこの方法でした。
　どちらがいいのでしょうか。


A.　 Q ＝ n C_P �儺 で計算した方が早いです。 C_P＝5/2・R を公式として覚えていても利用していないのは ‘ 宝の持ち腐れ ’ でしょう。

　入試問題では第１法則で誘導することが珍しくありません。それは P�儼 と U の式、さらに第１法則が使えるかどうか試したいからです。　ただ、多くの人がこれを正統的な解法と受け取ってしまっています。

　第１法則を用いる方法の良さは一般性があることです。定圧に限らず用いられます。
　定圧の P�儼 がダメになっても、P V グラフの面積 から仕事が分かる場合があります。




Q2.　定積変化での熱量の場合はどうでしょうか。


A.　定積変化での熱量も Q ＝ n C_V �儺 で計算するのがふつうです。
単原子なら、 C_V＝3/2・R ですね。

　定積では仕事が０であり、第１法則により Q＝�儷 として求めることもできますが、まず見かけません。　ところが、定圧は第１法則で求める人が多いんですね。　回り道であることに変わりありません。

　「 定積は 　Q ＝ n C_V �儺、　定圧も　Q ＝ n C_P �儺 」と セットにしておいてはどうでしょうか。
　単原子なら、 C_V＝3/2・R 、 C_P＝5/2・R です。
　そうでなければ、 C_V と与えられると思います。　 C_P＝ C_V ＋ R 　の関係に注意してください。

　ところで、 C_P のほうが C_V より大きい理由はいいですか？　論述問題でよく問われますよ。




Q3.　「エッセンス」で学びました。　定圧の場合は、気体が膨張して仕事をしているからです。


A.　内部エネルギー U は温度で決まり、温度を１K 上げるときの増加分 �儷 は定積でも定圧でも同じという認識がベースにあってのことですね。　第１法則によって、定圧の方が膨張での仕事の分だけより多くの熱量が必要になるのでした。

　 内部エネルギーは絶対温度に比例 は大切です。　式で表せば　U ＝αｎRT　のようになります。　単原子分子なら、α ＝ 3/2 ですね。




Add　Q4.　定積と定圧の熱量について、かなり分かってきました。　ただ、話の流れからすると、 C_P＝ C_V ＋ R 　の R が P�儼 に該当するように思えますが・・・一致していないのは？


A.　状態方程式 P V ＝ n R T から、圧力 P が一定のときは V は T に比例します。
　すると、　　　 　　P�� V ＝ n R �儺 　　（※）
　左辺に注目。　 P�� V は定圧での仕事！　それは n R �儺 に等しいのです。
　さて、モル比熱は、１モルの温度を１K 上げるときの話です。　ｎ＝１ と �儺 ＝１
　したがって、 P�� V はＲに等しいのです。

　「定圧では　仕事＝ P�� V ＝ n R �儺 」　直ぐに出せるようにしておきたい関係です。　定圧では という制限は忘れないように。

　 （※）　y ＝ a x　なら　�凾� ＝ a �凅 　　a：定数　　今の場合は　a ＝ ｎR/P






　





　

///////////　 電磁気　 ////////////////////////////////////////





Q.　力学と波動までは、つまり「エッセンス」の上巻まではそれなりに分かった感じがします。
　しかし、電気分野に入ったら、急に難しくなり、分かった気がしません。これから磁気分野に入るのですが、不安です。


A.　その実感はもっともですね。力学・波動に比べて電気は崖に出会うかのごとき段差があります。　３次元での認識が重視されることに加えて、正・負の電荷の存在が事態を複雑化しています。
　電気分野は　静電気（電場と電位）・コンデンサー・直流回路に分かれ、この順に習うのですが、実は理解しづらい順です。初めの方ほど理論的で、抽象性が色濃く、３次元的なのです。ガウスの法則はその最たるものでしょう。

　まず、直流回路のマスターをめざすのがいいでしょう。オームの法則は中学でも習ったことですし。「電位」の概念が目新しいのですが、回路は水路に、電流は水の流れに対応させるのが分かりやすく、電位は水路の高さを表す という見方ができれば、取り合えずＯＫです。

　次に、静電気かコンデンサーか、取り組みやすい方を。　多分、静電気の方が力学に近い分、取り組みやすいかと思います。
　コンデンサーには「親しみが感じられない」というのが自然な感情でしょう。物理としての重要度もそれほどではないと思えます（入試では重要ですが）。　ガウスの法則に基づいて説明されていますが、Ｑ ＝ ＣＶ と 電気量保存（電荷保存） に注目して学習することを優先してください。

　「すべて理解しなければ」とか、「理解しないと先へ進めない」とは考えないように。「分かりにくいところは適当に流す」のがよいと思います。そして、時々、振り返って考え直してみてください。
　あきらめずに努力していると、ある日、突然、視界が晴れるのです。ふと気が付いたら晴れていたということもあります。
　いろいろな教科の中で、物理に際立って起こる現象です。 「分かった！」という体験の積み重ねが 学ぶことの楽しさにつながります。







Q.　電場（電界）は何とか分かるのですが、電位 が分かりません。


A.　まず、力学を思い出してください。重力 ｍｇ のほかに位置エネルギー ｍｇｈ が必要でした。力を用いて運動方程式を立て、運動を調べるのが基本ですが、曲面上を滑る場合だと加速度が一定にならず、解けなくなってしまいました。　でも、エネルギー保存則なら対処できましたね。
　力と位置エネルギーのペアが大切です。　 ばねの弾性力 ｋｘ に対して 弾性エネルギー ｋｘ²/２ を用意しましたし、 万有引力に対しても位置エネルギーを用意しました。

　今は 静電気力による力学を扱いたい のです。　電場 E は静電気力 F 一歩手前の量です。電荷をｑとして、F ＝ ｑ E　これで静電気力が扱えます。E は ＋１〔C〕にはたらく力です。　次に用意したいのが静電気力の位置エネルギー U で、電位を V として、U ＝ ｑ V　と表せます。　電位は位置エネルギー一歩手前の量で、＋１〔C〕に対する位置エネルギーです。

　重力や弾性力に比べて静電気力は大きさも向きも複雑に変わるので、取り合えず電場 E と電位 V に代表してもらって、その実態は状況に応じて決めることになります。　高校では、一様電場と点電荷の２つのケースが扱われます。
　一様電場は静電気力が一定なので重力と似ていて、点電荷による静電気力はクーロンの法則にしたがうので、万有引力に似ています。

　ｑ E は力のつり合いや運動方程式で用い、電場中の運動ではエネルギー保存則、
　 ｍ ｖ² /２ ＋ ｑ V ＝ 一定　で 電位 V が輝きます。

　静電気力による力学と言いましたが、「コンデンサー」からは純粋に電気の話に入ります。　　でも、電場 E と電位 V は電磁気全体を通して活躍します。






Q.　F ＝ q E　と　U ＝ q V　は 無条件で成り立つもので、
　　 　　E ＝ ｋQ / r²　と 　V ＝ ｋQ / r　は「点電荷 Q 」に対する式なんですね。


A.　その通りですが、 前者は 電荷 ｑ の帯電体に働く力 F とそれがもつ位置エネルギー U の話で、後者は 点電荷 Q が周りにつくる電場 E と電位 V の話です。 内容がまるで違いますからね。

　電位はスカラーで、電位に関する　U ＝ ｑV　と　V = ｋQ/r　は符号付き であることにも注意してください。
　電場はベクトルで、電場に関する　F ＝ ｑE　と　E ＝ ｋQ/r²　は 大きさ、つまり、絶対値の関係です。

　電磁気の公式の大半は絶対値の関係です。　電磁誘導の法則や自己・相互誘導でマイナスを用意するのは、誘導起電力の向きを表すための便宜的なものです。
　純粋な意味での符号付き公式は、U ＝ｑV と V = ｋQ/r に限られます。　V は電位ですが、この２つ以外の公式で登場する V は電位差（電圧）です。
　電位は ある点での値であり、電位差は ２点間でのもの です。

　あと ひとこと。　電位は、０とする基準が必要 で、 V = ｋQ/r の基準は 無限遠点です。　忘れないように。






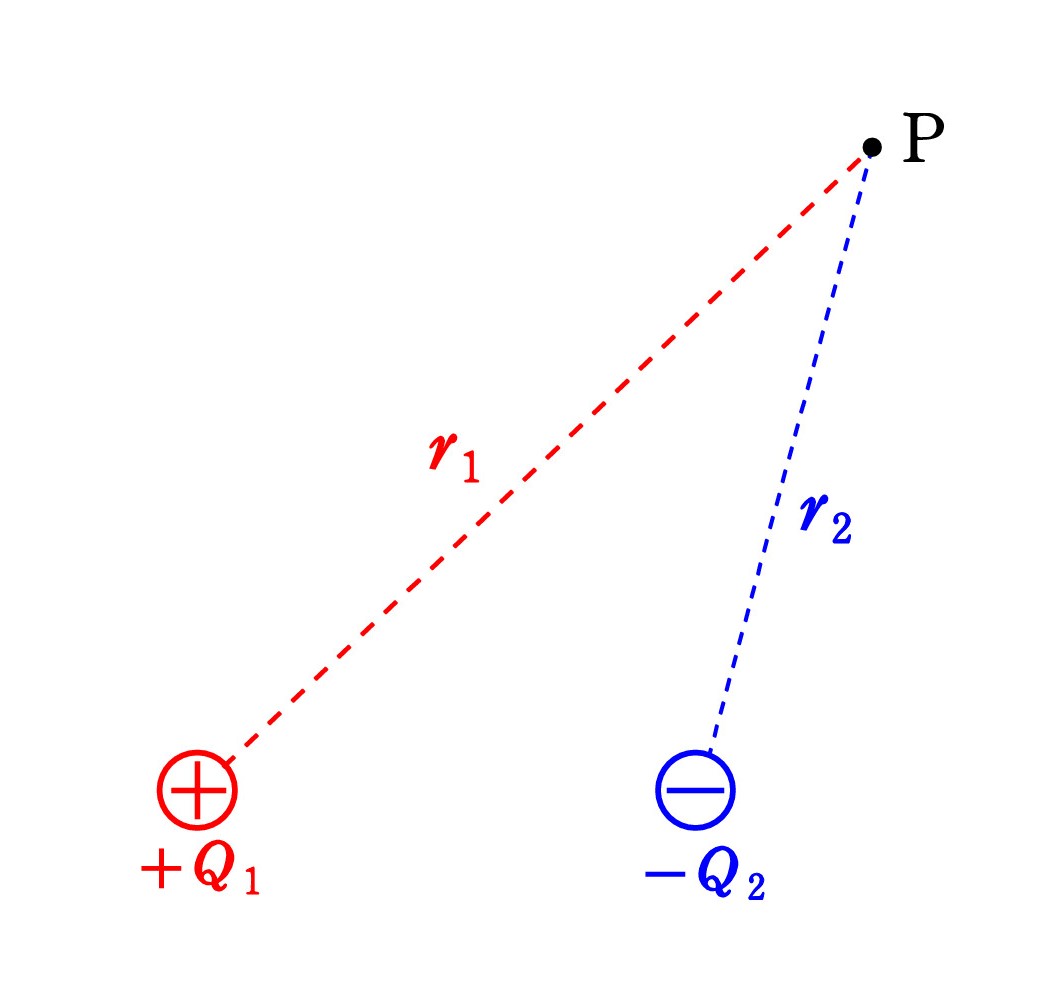Q.　点電荷の電位の公式　V = ｋQ/ｒ で Q には符号が含まれるというのは分かります。しかし、いくつかの点電荷があるときに、電位は足し算 でいいという理由が分かりません。
　たとえば、＋Q₁ と−Q₂ があり、それぞれからr₁ 、r₂ 離れた点 P の電位が　V ＝ ｋQ₁ /r₁ ＋ ｋ(−Q₂ )/r₂　と、和になる理由は何でしょうか ？


A.　電位は位置エネルギーにつながるものでした。より正確には、＋１Ｃ のもつ（静電気力による）位置エネルギーです。　位置エネルギーは足し算ができます。力学でも、重力のもとでばねが伸び縮みしていれば、ｍｇｈ＋ｋｘ²/２ としていたでしょ。　異種の位置エネルギーでさえ、足し算できるのです。　同種の ｋQ/ｒ ができないわけがありません！

　U ＝ ｑV で完全な位置エネルギーです。　静電気力に加えて、重力も働いているケースなら、　ｑＶ ＋ ｍｇｈ で位置エネルギーが用意できます。　さらに、ばねまで関連していれば ｋｘ²/２ を加えればよいのです。　それぞれの基準点はバラバラで構いません。

　位置エネルギーは、基準点まで移動する際の 力がする仕事で決めます。複数の力がある場合、「合力の仕事」＝「それぞれの力の 仕事の 和」という関係を証明し、それに基づいて説明するのが本来ですが、今は深入りは避けましょう。

　





Q.　一様な電場 での公式は Ｖ ＝ Ｅｄ と「エッセンス」ではなっていますが、　学校では Ｅ ＝ Ｖ/d です。　教科書には両方が併記されています。 数学的には同じですが、物理としての優先順はどうなっているのでしょうか ？
　

A.　Ｖ ＝ Ｅｄ が 優先 します。　一様な電場 Ｅ では、２点間の電位差 Ｖ がどう表されるか、が理論的な話の流れです。　Ｅ が先で、Ｖ が後なのです。　電場を習ってから電位を習うように、電場があるから電位がある と論理は展開しています。　力があって位置エネルギーが決まる のです。

　実用的には、コンデンサーの極板間電圧 Ｖ が分かっていて、極板間の一様な電場 Ｅ が知りたいということが多いので、Ｅ ＝ Ｖ/d を公式として重視する人もいます。　これだと Ｖ があるおかげで Ｅ があるように見えてしまいます。

　極板上の電荷 Ｑ が電場 Ｅ をつくり、次に電位が（基準点を設けることによって）決まり、２点間の電位差 Ｖ が定まる と理解したいのです。　ｄ は電場方向の距離であること、電場に垂直な平面は等電位面 であることにも留意してください。
　ささいなことですが、Ｖ ＝ Ｅｄ と Ｅ ＝ Ｖ/d は 数学的に全く同じではありません。　前者なら、ｄ＝０ も含みますが、後者では無理です。

　でも、 Ｅ ＝ Ｖ/d と覚えたのなら、それで構いません。






Q.　コンデンサーの２枚の極板には ＋Ｑ と −Ｑ の電荷があるので、極板どうしが引き合うのは分かります。
　問題はその力 Ｆ の性質です。「エッセンス」（下）ｐ68 (新版 p73) には「 Ｑ が一定なら、Ｆ は極板間隔によらず 一定 」となっています。　これは電気分野の根本法則であるクーロンの法則に反しています。　クーロンの法則は 距離が離れると力は弱くなると明言しています。


A.　まず、クーロンの法則は点電荷に対するもの です。　確かに、点電荷どうしでは、間の距離の２乗に反比例して、力は弱まっていきます。　ところが、極板上の電荷は 面上に分布しています。それが極板間引力 Ｆ が極板間隔 ｄ によらなくなる最大の理由です。

　ただ、もう一つ見落としてはいけないことがあります。　　コンデンサーの大きさに比べて十分小さい間隔 ｄ の場合を扱っていることです。 それによって 極板間の電場が一様 として扱えています。　間隔 ｄ を大きくしていくと、電気力線が曲線となって極板間からはみ出し（エッセンス（下）ｐ45 (新版 p50)）、電場は一様でなくなり、Ｆ は弱くなっていきます。

　十分に遠くに離せば・・・もはや極板の大きさは気にならず、２つの点電荷のケースに該当するようになり、まさに クーロンの法則に従います。
　「十分遠くなら、点電荷どうし」・・・この見方も大切 です。　物理らしい考え方でしょう。

Q.　オームの法則 ですが、「エッセンス」は Ｖ ＝ ＲＩ としていますが、 Ｉ ＝ Ｖ/R で習っています。　使用している教科書では両方とも書かれていますが、Ｉ＝Ｖ/Ｒが先に書いてあります。


A.　キルヒホッフの法則 への発展を考えたとき、Ｖ ＝ ＲＩ が優ります。　閉回路に対して、（起電力の和）＝（電位降下ＲＩの和）が成り立つというのが、キルヒホッフの第２法則ですね。　オームの法則を含んでいます。
　さらに、Ｉ ＝ Ｖ/Ｒ だと Ｒ＝０ のとき困ります。 　Ｖ ＝ ＲＩ には、抵抗Ｒ に電流Ｉが流れるときの 電位降下を表すという役割もあります が、抵抗のない導線では、電位降下は起こらないという確認にも Ｒ ＝ ０ を含めたいのです。 　Ｖ ＝ ＲＩ だけを書いている教科書もあります。

　割り算型より掛け算型の方が覚えやすく、間違えにくいことも利点です。　割り算型では、分母と分子を逆にする可能性が出てきます。　それは、一様電場の公式 Ｖ ＝ Ｅｄ が Ｅ ＝ Ｖ/ｄ より優れている理由の一つにもなります。

　掛け算型でも　Ｖ ＝ I Ｒ とはしたくありません。　先生の中でもそう書く人がかなりいますが、数学で ｙ ＝ a x と書くように、定数は前に出したいのです。　R が定数で、I が変数です（ふつうは)。　 何が定数で、何が変数か の認識はとても大切 です。






Q.　電磁誘導についてですが、　導体棒が 磁場中を速さ v で動くときの 誘導起電力 V の公式で 　V = v B l　があります （B：磁束密度、ｌ：棒の長さ）。　学校では、ファラデーの電磁誘導の法則ですべて解決できるので、公式などいらないと教わりましたが、「エッセンス」では用いていますね。


A.　確かに、電磁誘導の法則だけですむ――というのは物理学としては正しいですし、その認識は大切でしょう。　ただ、入試では限られた時間内に解答しなければなりません。
　V = v B l は公式、つまり公（おおやけ）に認められたものですから、利用しない手はありません。　誘導起電力の向きも即断 できます。
　電磁誘導の法則から進むのは、100m競走で、10m後ろからスタートするようなものです。

　 V = v B l の導出は 電磁誘導の法則以外に、電子に働くローレンツ力から理解できることも、この公式を重んじたい大きな理由です。 そして、回路のどこがどのような「電池」になっているのかを明確にしてくれます。





Q.　導体棒の誘導起電力は V＝ｖＢｌ を用いています。　ただ、誘導起電力の向きの決め方を確認したいのです。　導体棒を起電力Ｖの電池に置き換えるとき、棒のどちら側が正極(＋極)になっているかということです。
　教科書だと、レンツの法則、つまり、磁束の変化を妨げるような電流の向きを考えて決める、あるいは、ローレンツ力の向きを考えて決めるとなっていますが、いずれもとても手間がかかります。　簡便な決め方として、学校ではフレミングの右手の法則を教わりました。　なぜ、教科書に書かないのでしょうか。


A.　昔の教科書は 右手の法則を扱っていました。　しかし、電磁力の向きを決める左手の法則との混同が起こりやすいことなどからでしょうか、 今は書かれていません。
　そうは言っても、簡便法は必要です。　「右ねじ」を勧めます。　「エッセンス」のコピーを下に付けておきます。「ちょっと一言」のところです。　棒を ねじ と思って、ｖ から Ｂ へとねじを回すので、公式は ｖＢｌ の形で覚えます。
　慣れると、頭の中でねじを回せます。　「進み」だけでなく、「ゆるみ」も利用できるようになると、本当に早いですよ。
　言い遅れましたが、近い側で(ｖとＢの間の角度が小さい側で) 回してください。

• 「エッセンス」のコピー

　言うまでもないかもしれませんが、　電池に置き換えれば、次は 直流回路の問題 という 解法戦略 が大切です。

　電磁力 Ｆ＝ＩＢｌ についても フレミングより 右ねじ が優ると思います。　Ｉ から Ｂ へと ねじを回します。　やはり、「進み」だけでなく、「ゆるみ」も利用できます。





Q.　女子です。　ドライバーを使ったことがないので、右ねじの回し方がピンときません。　だいたい「右ねじ」とは どんな ねじ なのでしょうか？


A.　 確かに、ドライバーでねじ釘を板に食い込ませた経験がベースになっていますね。
　でも、ペットボトルのキャップをはめるとき、どちらに回しながらはめていくかは 迷わないでしょう。　キャップの動きは右ねじと同じです。
　右ねじ(キャップ)をつかんだ感じで、実際に手を動かして慣れてください。 「進み」では時計回りに手を回しながら腕を突き出し、「ゆるみ」では逆回りで腕を戻します。　10往復ぐらいで身に着くでしょう。　　初心者は「進み」だけを と言われていますが、「ゆるみ」までマスターできるのではないでしょうか。

　日常出会う ねじ はどれも右ねじと思っていいです。　右回り(時計回り)に回すとねじが進んで締まります。
　左ねじ(逆ねじ)はまれで、扇風機など回転部分で使われていますが、無視してください。


　それでも、ねじが苦手という人もいるでしょう。　すると、電磁力の向きは左手で決めているはずです。　 V＝ｖＢｌ に対しても、左手で対処できます。　中指を導体棒の速度ｖの向きに合わせれば、親指が誘導起電力Ｖの向きです。
　人差し指はいつも磁場Ｂで、親指が求めたい向き(電磁力か誘導起電力という 力の付くもの の向き)です。　　　　　　　　　　起電力は電圧であって、力ではないのは、言うまでもないこと。

　３本の指を合わせようとすると、迷いやすいので、人差し指と中指の２本を合わせ、最後に親指を立てるといいですよ。


　右ねじにしろ、左手にしろ、電磁力は (電流が流れる)導体棒に垂直に、誘導起電力は 棒方向になる ことも 意識しておくと間違えにくいでしょう。








Q1.　電磁力 Ｆ＝ＩＢｌ を習ってから 誘導起電力 V＝ｖＢｌ を習ったので、電磁誘導の問題に出会うと、つい、電磁力から考えるのかと思ってしまいます。　そうではないんですね。


A.　ふつうは、磁場中で導体棒が速度ｖで動かされて誘導起電力Ｖが発生し、回路に電流Ｉが流れ、導体棒は電磁力Ｆを受ける――という筋道です。　これがスタンダードと思ってください。
この場合、電磁力Ｆはブレーキになります。

　変則としては、本当の電池が回路に電流を流し、静止していた導体棒にも電流Ｉが流れ、電磁力Ｆによって導体棒が動き出す場合があります。　速度ｖを得た導体棒は電池に変身します。　本当の電池が電流を流すのを妨げる向きに誘導起電力が生じるので、電流は弱まります。　逆起電力と呼ばれる状況です。

　一般に 電磁誘導では、事態は収束する方向に向かいます。　時間的に変わらない状態へと向かうのがふつうです。　変化が続くとしても、穏やかな変化に向かい、破滅的な事態にはなりません。　「磁束の変化を妨げる」という 電磁誘導の法則に基づいているからです。
　




Q2.　今までに出会った問題では、磁場中の導体棒は十分に時間が経つと、等速度運動になっていました。


A.　ふつうはそうですね。　やがて摩擦などによって静止することもありますが、静止は等速度に含まれますから。
　ただ、例外なくというわけではありません。　回路にコンデンサーが入って等加速度運動になるケースや、コイルが入って単振動になるケースもあります。

　回転する導体棒だと、角速度一定の等速回転に入るのがふつうです。

　問題を解くとき、「ふつう」を意識していると、見通しが立てやすいのは確かです。　「ふつう」でなければ、誘導設問に従って考えていけば、どのような運動になるか、分かるはずです。







Q.　「電磁誘導ではエネルギー保存則にも気を配りたい」とのことですが、　エネルギー〔 J 〕そのものではなく、　（外力の仕事率）=（抵抗での消費電力）のように、１秒間当たりの 仕事やエネルギー〔W〕に、つまり、J /ｓ になっているのはなぜですか。


A.　磁場中で導体棒に外力を加え、一定の速度で動かすようなケースですね。　あるいは、電磁力で動き出した導体棒が一定の速度に達したケースも同様です。現象が連綿と（ズーッと）続くので、単位時間当たり（1秒当たり）で、エネルギーの出入りを表すことになります。

　力学や熱力学あるいはコンデンサーなどでは、現象に出発点と到達点があるのがふつうなので、その間のエネルギーや仕事を考えています。
　電磁誘導に限らず、電流が流れ続ける直流回路だと、単位時間当たりになっています。（電池の供給電力）=（抵抗での消費電力）のように。　移り変わりゆくエネルギーの流れを表している のです。






Q.　電磁誘導などでエネルギー保存則を用いるとき、保存則を表す公式がないのが気になります。　何となくこうなるだろうという直感で書いているのですか。


A.　それに近いです。関連するエネルギーを確認し、このようなつながりになるはずだという洞察力に基づいて書いています。　エネルギーに見落としがないかどうかと、エネルギーの移り変わりに注意を払います。　もちろん、仕事も考慮してのことです。　コンデンサーの場合も含めて 電磁気でのエネルギー保存則は洞察力の世界 と言っていいでしょう。　顔を出すエネルギーや仕事の種類は限られているので、関連付けるのは、経験つまり慣れですね。

　外力の仕事は「正」と仮定して、つまり、エネルギーを供給しているとして式を立てると分かりやすいでしょう。　筋道の通ったつながりが大切で、正だと思っていた項が負であっても構いません。　外力の仕事は負になると分かっていても、あえて正として立式することがあります。

　電池のする仕事 Q V（単位時間当たりなら電池の供給電力 V I ）も正と仮定して保存則を書くことが多いですね。　正電荷が電池の負極側から正極側に通るとき、あるいは電流が正極から流れ出るときが正です。　電池が回路にエネルギーを供給している状況です。
　　　　　　　　　　　　　　　　（ Q ：電池を通過した電気量、 V ：電池の起電力、 I ：電流 ）





Q.　磁場中で導体棒が動き、誘導起電力によって電流が流れる場合の電磁誘導ですが、エネルギー保存則を考えるときに、電磁力の仕事が入っていません。
　たとえば、磁場中に長方形コイルを引き込むとき、「外力の仕事」＝「ジュール熱」となっていますが、コイルを流れる電流によって電磁力が働いているはずです。　その仕事を無視してよいのでしょうか ？


A.　電磁力は重要な力です。力のつり合いや運動方程式などで活躍します。　でも、エネルギー保存則では「電磁力の仕事は考えなくていい」のです。

　もし、考えるのであれば、誘導起電力の仕事も同時に考えることになります。　導体棒は電池に変身し、（電池がエネルギーを出すように）電池のする仕事があるのです。
　そして、両者の仕事の和は０になるのです。　電磁力も 誘導起電力も 自由電子に働くローレンツ力 に基づいており 、ローレンツ力は 仕事をしない からです。　ローレンツ力は 電子の速度の向きと直角をなして働く からですね。

　理解しがたいかもしれませんが、これからは「電磁力の仕事」を頭から消し去ってください。　多くの人達が（先生方も含めて）気づかないまま 無事 通り過ぎている・・というのが実情です。
　なお、『Ｑ＆Ａ 名問の森』で、より詳しく説明しています。





Q.
A.

　　








【質問について】　メールでの質問は次のアドレスまで。　　　　hiroba@mb.ccnw.ne.jp

　　　　　　　　　手紙またはFAXでの質問は河合出版を通してください。電話は、正確に伝わらないことが
　　　　　　　　　ありますので、できるだけ避けてください。

トップページに戻る