Q＆A 良 問 の 風
構成： 入試一般 ・ 力学 ・ 熱 ・ 波動 ・ 電磁気 ・ 原子
今回の加筆（New）： 熱（連続の２項目）
New をクリックすると、直近の加筆に移れます。
「エッセンス」・「森」は本そのものを表し、『Ｑ＆Ａ エッセンス』・『Ｑ＆Ａ 森』はこのホームページの記事を表しています。
構成： 入試一般 ・ 力学 ・ 熱 ・ 波動 ・ 電磁気 ・ 原子
今回の加筆（New）： 熱（連続の２項目）
New をクリックすると、直近の加筆に移れます。
「エッセンス」・「森」は本そのものを表し、『Ｑ＆Ａ エッセンス』・『Ｑ＆Ａ 森』はこのホームページの記事を表しています。
三訂版が刊行されていますが、旧版(改訂版)を用いている人が多いので、問題番号は旧版に合わせています。
三訂版については、括弧つきで（新版）として番号を記しています。
三訂版は 旧版に対して、入試問題を共通テストを中心に６題増やし、
論述問題（小問題）を３題増やしています。
入試一般 //////////////////////////////////////////////////////////////////////////////////////////////
Q. 赤本はいつから始めればいいですか？
A. 受験の２か月ぐらい前からで十分間に合います。 赤本は志望大学の問題の難易度や分量などを確認するためのものです。物理に関して言えば、赤本は腕試し用です。 実力を伸ばすためには選び抜かれた入試問題集を使ってください。
赤本にはろくな問題が載っていません(赤本のせいではなく、大学のせいです)。 学習用としては不向きなのです。 どんな問題であれ、やればそれなりの効果はありますが、かけた時間に対するコスパ（cost performance）が悪いのです。 もちろん、教科によって赤本の評価は異なります。
難易度や分量は早い時期からチェックしておくのは意味があります。難しい問題ばかり登場してビックリするかもしれません。皆できないので、あまり気にしないことです。
赤本に限らず、合格のための得点や得点率が書かれている場合、高過ぎる値と思っていいでしょう。そんなに解けなくても…というのが実態です。
Q. 物理の学力が同じでも試験の得点には違いが出るという話を聞きました。本当でしょうか。
A. 本当です。声を大にして言いたいです。現在、多くの大学が解答時間内には解ききれない問題量を課しています。すると、要領よく得点できるかどうかがポイントになります。
まず、解ける設問に全力を集中してください。難しい設問は時間を失わないよう適当にスキップします。 とにかく全体像を早く把握することです。 そして、スキップした設問に戻りますが、比較して解けそうな設問を選びます。 塗り絵を塗るように、塗りやすいところから広げる 要領です。
設問ごとの難易度を基本・標準・応用・難と分けてみると、標準の設問数が多く、従って配点が大きく、ここで点差がつくのです。 応用がある程度こなせれば十分です。 難問にこだわらないように。たとえ解けても、かかった時間に見合う配点にはなっていません。 合否は標準問題で決まるといって過言ではありません。
模試の採点をしていると、大問３題のうち、初めの２問はよくできているのに、第３問目は白紙という答案に出会うことがあります。現役生ですね。時間切れを起こしているのです。第３問目には解けたはずの設問がいっぱいあっただろうにと…と思わずにはいられません。
計算欄があれば、解けなくても分かった範囲のことは書くべきです。部分点を狙うのです。基本的に加点法なので、間違ったことを書いてもマイナスにはなりません。 選択肢があれば、分からなくても選びます。正直な人にはつらいかもしれませんが、「カンも実力のうち」と割り切ってください。
次に、見直しをしっかりやってください。 私自身、できたと思った設問でボロボロうっかりミスをしています。見直しの時間はしっかり確保すること。 60分の試験時間なら 10分前になったら見直しに入ること。まだ解けていない設問に取り組んだ方が点が増えるというのは錯覚です。 試験が終わるたびに「ケアレスミスをしてしまった！」と叫んでいませんか。防げたはずのミスです。
短い時間できちんと見直すには平素からの訓練が必要です。計算の途中経過は消しゴムで消さないで、すべて残しておくこと。 思い違いに気づいた時、修正が簡単に済みます。 ある設問の結果を次の設問で用いるときにはすぐに見直します。 計算をもう一度やるのではなく、計算の記録を 目で追います。
問題文を読み違えていないか、条件を読み落としていないか、指定文字で解答しているか、次元は大丈夫か、など注意すべきことは一杯あります。
Q. 次元のチェックが大切だとよく耳にします。でも、もう一つ有用性がピンときません。
A. 次元（ディメンション）がどのようなものかはエッセンス(上)p151で確認してください。計算ミスを防ぐのに役立ちます。
結果だけでなく、計算の途中でも次元に気を付けます。足し算と引き算は同じ次元でしかできませんし、式の両辺の次元は合っているかとかです。 ただ、単位にまで戻って調べるような時間のかかることはしないように。 セットで見ます。 ｍｇ や ｋｘ なら、力ですし、ｍｇｘ や ｍｖ２ なら、エネルギーです。
√(g×長さ） が速さを表し、√(長さ/g) が時間を表すことを知っておくと、力学ならほとんどのケースで次元がチェックできます。 前者は高さｈだけ自由落下するか、滑らかな曲面を高さｈだけ滑り降りたときの ｍｖ２/２＝ｍｇｈ から求めた ｖ＝√(２ｇｈ) で覚えておくと、答えとして使える場合も多く、便利です。 後者は長さ l の単振り子の周期の公式 T ＝ 2π√（l/g） を思い出すことです。
共通テストや多くの私大が選択肢タイプです。 解けなくても候補は次元で限定できます。 共通テストの前身であるセンター試験では一つに絞れたケースさえあります。
次元のチェックは数学にはない物理独特のもので、大変効果的です。 数学はモノトーンの世界ですが、物理はカラーの世界です。物理量ごとに色が異なっているのです。 次元のチェックで私自身何度救われたことか。これをしない予備校講師はいないと言っていいでしょう。
Q. 答案用紙の計算欄にはどの程度詳しく書けばいいでしょうか。 問題文で登場していない物理量には 定義をきちんと書くように指導されていますが、丁寧に書いていくと いつも時間がなくなります。
A. 大切なのは、用いた法則とそれに基づいた式でしょうね。
「運動量保存則より (ｍ＋M)ｖ＝・・・」といった具合です。途中計算は問題文の余白などですませます。 慣用の文字であれば、「求める速度をｖとして」というような定義は書かなくてよいと思います。計算欄は一般に狭く、書くスペースの確保に苦労します。
何より 時間を急ぎたい のです。 解答時間は本当に短いのです。 最後に、もし、時間が余れば、定義を付け加えます。書くスペースがなければ、(注1)とでもしておいて、別のところに書く手もあります。
入試では、見直しなどに追われ、時間が余ることはないのが実情でしょう。
先生に「定義を書く必要はありますか」と尋ねるのは、警察に行って「車が来ないから、赤信号だけど渡っていいですか」と尋ねるようなもの、と言っては言い過ぎでしょうか。
解決のキーポイントは書くべきです。 たとえば、「全運動量は０だから、2つの物体は反対方向に動く」などです。 また、考え方を文章で説明するのは大変で、図を描いた方が早いということはよくあります。 もっと図を利用しましょう。 図に文字を入れれば、自然に定義できてしまいます。衝突なら、衝突後の２物体を描き、速度の矢印に ｖ や V を付けておけば十分でしょう。何より、自分にとって役立ちます。
採点者はあなたが分かっているかどうかを見たいのであって、要点だけでいい のです。 参考書の解答のように整然としたものを書く必要はありません。採点は基本的に加点法で、定義がないから減点ということはまず考えられません。もちろん、問題文で指示があれば別ですが。
Q 図を描く大切さは、理科の中でも物理が際立っているように思えます。
A. そうですね。 すべての教科の中で と言ってもよいかもしれません。
図の役割として、複雑な問題状況に出会うと、図を描きながら頭の中を整理し、何が本質的なことかをつかんでいくというステップもあります。
一見、複雑に見える現象から、余分な部分を切り捨て、本質部分を抜き出していく のです。 まさに 図を描いて考える のです。 「式より図」です。
難問題を解く手掛かりは、往々にして、図による状況の把握から得られます。
また、長い計算で苦労して得た結果が 一つの図解で説明できることもあります。 まさに 図の醍醐味 が感じられるときです。
Q. 共通テストでは「思考力」が重視されています。 図で考えるのは、思考力の養成に役立つということですね。
その他にも思考力を養う方法について知りたいです。
A. その通りです。 どんな図にするかと、どんな風に考えているのかとは不可分です。 記述答案の採点時でも、図を見ただけで、問題が解けているかどうか、見当がつきます。 図の重要さを認識しているかどうかは、実力のバロメーターと言えます。
また、問題を解いたとき、答えを合わせて終わりではなく、解説をていねいに読んでください。 論理的な思考力を育てるのに、大きな効果があります。 法則の適用や分析などの 論理のつながりを意識して読んでください。 国語力もつきます。 「問題が解ける」を超えて、「人に説明ができる」ことが大切な力です。
個別入試では論述力が問われることも多いのですが、まずは読解力です。
別解があれば、しっかり検討してください。 気づかなかった視点は今後に役立ちます。
「ナルホド！」という感激。 小さなものでも 貴重な財産です。
「なぜ？」という問いかけは、物理ではとりわけ大切 です。 思考力は自然に鍛えられていきます。 問題を多く解くことも大事 です。 間違えることを恐れないように。 間違えるたびに、「なぜ？」が生じ、解決できるたびに「分かった！」となります。 その感動の積み重ねが学問の原動力です。
Q 「思考力」を強調する問題集がいいのでしょうか。
A. 教科書を規定する学習指導要領の理念として「思考力」が強調されるようになったため、最近の問題集はタイトルに「思考力」を入れたり、個々の問題に対して「思考力を問う問題」という評価をラベル貼りすることが多くなっていますが、単に「難問」を言い換えただけのケースばかりのように思えます。 あまり気にしない方がいいでしょう。 もともと、物理の問題はすべて（と言ってよく）思考力を問うものです。
計算を伴わない、定性的な問題の方が物理としての思考力を効果的につけてくれます。 典型タイプは一問一答型です。 共通テストで言えば、第１問の小問集合で、上位の人が意外と足をすくわれています。 図 や グラフ を素材とした問題はその好例 です。
「良問の風」の巻末近くにある「論述問題」は理解を深めるためのものですが、定性的な思考力も鍛えてくれます。 まとめてではなく、折りに触れて楽しみながら進めてください。
Q 「思考力」という言葉は余りにも漠然としています。 思考力が大切なのは分かりますが、もう少し具体的にできないのでしょうか。
A. 私も「思考力」と聞くたびに鼻白む思いがします。 学力の実体をほとんど何も言っていないからです。 物理の場合、「推論力」ではどうでしょうか。 論理的な道筋をつけて答えに到達する力です。
「Why ＋ How」と言ってもよいかもしれません。「なぜそうなるか」と「いかにして導くか」の協調です。 定性的な問題は Why が濃く、計算問題は How が濃いと言えるでしょう。
Q 記述模試（２次・私大対象）では良い成績なのに、マーク模試（共通テスト対象）では芳しくありません。 何が問題なのでしょうか？
A. 簡単に言えば、計算問題は得意なのに、定性的に判断する問題が不得手なのではないでしょうか。
マーク模試では定性問題がよく顔を出します。 大小の比較だったり、グラフや図の選択、文章の正誤などなど・・・。 とくに、第１問、小問集合に多く現れます。 定性問題での失点が原因かどうか確認してください。
かつて調査したことがあるのですが、記述模試で偏差値65以上の中で、マーク模試の偏差値が10以上下がってしまう人が少なからずいました。 答案を確認すると、まさに定性問題での失点が原因でした。
定性問題に弱いということは、物理が本当には分かっていないということ です。 つまり、上位を目指す人にとっては深刻な状況です。 公式をいかに運用するかだけに気を取られないようにしてください。 定性問題では、頭の中での論理の組み立て が問われています。
Q. 文字式で答える問題では、単位を付けるのですか。
A. 問題文に単位が書かれているときは、答えに単位を付け、（ ）か〔 〕でくくります。
ただし、「速さ v〔 m/s 〕を求めよ」のように、すでに単位が書かれていれば、不要です。
単位は 簡潔で常識的なものを書いてください。 たとえば、エネルギーは〔 J 〕で、
〔 N ｍ 〕とはしないように。 内容は正しいのですが、〔 J 〕を知らないと判断して、減点する採点者もいます。
一方、問題文に単位が書かれていないときは、単位を付けてはいけません。単位が決まらないからです。〔 m/s 〕ではなく、〔 cm/ｓ〕かもしれません。
Q. 問題文で「答えはａとｂを用いて表せ」となっている場合、ａとｂだけで表せということでしょうか。それとも、ａとｂは用いた上で、他の文字の使用も可能なのでしょうか。
A. ふつうは、ａとｂだけで表すと思っていいです。
ただし、「ａを用いて表せ」のように、一文字だけのケースは、ａを答えに含め、他の文字も使用して答える場合があります。 ａがすでに判明し、ａへの代入作業を省きたいとき（代入すると式が複雑になるとき）に用いられます。あるいは、ａで誤っても、次の答えに連動させない配慮の場合もあります。 一文字と言いましたが、質問のケースも該当するかもしれません。
このように「用いて表せ」はあいまいな表現ですが、多用されています。 文脈で判断するほかはありません。
判断に困る場合もありますが、答えの内容が正しければ、採点時に配慮されるので、あまり悩まなくてよいでしょう。
Q. 問１で「長さｄを求めよ」となっている場合、問２以下の答えに文字ｄを用いてよいでしょうか。問１の結果を代入すべきか、迷います。
A. 確かに、解答の文字指定がない場合には迷います。一般的には、途中で現れた文字は用いていい です。ただ、代入すると、答えの表記がシンプルになる場合は、代入するのが自然でしょう。
出題者は、問１で誤っても、問２以下に連動しないようにｄを提示してくれることもよくあります。問１の答えに自信が持てないのなら、ｄを用います。迷うケースは両方書く手があります。
やや特殊なケースとして、計算欄（導出欄）があり、小設問ごとに求める量に文字を与えてくるのは、受験者全員に共通の文字を使用させ、採点しやすくするためのものです。最終設問に文字が割り当ててあれば、間違いなくそうです。この場合は、代入した方がよいでしょう。
ともあれ、内容が正しい答えには、採点時に配慮がなされるはずです。
Q. 力学の問題で、重力加速度 ｇ が与えられていませんが、答えには必要というケースに出会いました。どう対処すればよいでしょうか。
A. 出題者のうっかりミスと思われます。 ｇ を用いて構いません。心配なら、「重力加速度を ｇ として」と書き足せば万全でしょう。 ついでですが、「重力加速度の大きさを ｇ として」とすべきでは という質問も受けます。 確かに教科書はそう書いていますが、ｇ は大きさに決まっているので、「の大きさ」を省略しても構いません。
クーロンの法則を扱う問題で 比例定数 ｋ を与え忘れた入試問題もあります。当然用いる重要な定数は 意外に与え忘れが発生しています。 多くの作成者が関わる有名大学でも起こっています。
熱力学での気体定数 Ｒ でも起こっていますが、 ｎＲＴ の形は状態方程式で ＰＶ に置き換えられるので、こちらはちょっと注意が必要です。
Q. 入試まであと２週間です。何か勧められる勉強法はありませんか？ ＜入試直前＞
A. 新しい問題を解くのはもう止めましょう。ひたすら復習 です。 まずは頭の中を整理しましょう。「エッセンス」は終わったと思って本棚に置いていませんか。 要点は 大きな活字や太字 になっていますから、身についているかどうか確認していってください。
次に、「風」の問題編の まとめ で整理し、最後に解答・解説編の KEY POINT でチェックできます。
そして、機会あるごとに――電車の中とか――「エッセンス」をパラパラ見る ことです。適当にページを開いて。 本当に効果的です。１分間でもいいので。
また、今までやってきた問題には 間違えた設問 がマークしてあるはずです。それが あなたにとっての大きな財産 です。 もう一度解き直すのではなく、ミスの原因が思い出せれば、それで OK 。 思い出せなければ、答えを見て確認しましょう。
復習モードに入るのは、２次・私大なら２週間前、共通テストなら１週間前が目安でしょう。
もちろん、自分なりの計画を立てて進めているのであれば、それでいいです。ここに記したことは参考に留めてください。
Q. 物理は、力学・熱・波動・電磁気・原子に分かれていますが、入試ではどの分野を重視すればいいでしょうか。 ＜入試直前＞
A. 力学と電磁気は必出 と思ってください。 そして、電磁気で大きな差がつきます。現役生が弱いのも電磁気です（高卒生も強いとはとても言えない！）。 電磁気が入試の天王山 と言っていいでしょう。
一方、原子を出す大学はかなり限られています。志望大学の過去の出題状況を確認してください。 そこで、以下は原子を抜きにしての話です。
３題か４題の出題が多いのですが、出題数が３題の場合は、力学・電磁気に加えて波動か熱のどちらかになります。波動の方が物理としての内容がはるかに豊かであるため、波動が選ばれやすいと思われがちですが、現実の出題頻度は似たようなものです。
波動に比べて、熱（主には熱力学）の方がマスターに要する時間がグッと少なくてすむことに注意してください。問題パターンが限られているのです。 しかも、熱は苦手とする人が多く、点差がつきやすい分野です。 つまり、熱は「お得感のある分野」なのです。
入試では、熱をもっと重視した方がよい でしょう。 ４題（以上）の出題なら、必出に近いわけですし。
Q. 物理の公式は知っていても、問題に対してどう対応すべきか分からないことがあります。解く方針あるいは戦略と言ったらいいでしょうか、そのような点での重要事項が身についているかどうか、少し不安です。 ＜入試直前＞
A. 問題を見た時なすべきは、まず 状況の把握（あるいは、現象の認識）であり、
次に、解く方針を決める ことですね。 公式を用いるのはそれ以後の話です。
解法の方針について、かつて雑誌に掲載したチェックドリルがあるので、試してみてください。
Q. 物理が苦手です。 入試まで時間もないのにどうしたらいいでしょう。 ＜入試直前＞
A. 物理がかなり不得意だという人は、範囲を思い切 ってしぼることです。
頻出項目 を、以下、列挙してみると（青が優先）、
力 学 ・・・ 放物運動・エネルギー保存 ・運動量保存 ・円運動・単振動
熱 ・・・ 定積・定圧・等温・断熱変化
波動 ・・・ 弦と気柱の定常波・ド ップラー効果・光の干渉
電磁気 ・・・ コ ン デンサー・直流回路 ・電磁誘導・電磁場中の荷電粒子の運動
以上の範囲で、まず、「エッセンス」の例題（Ｅｘ）ができるように頑張ってください。 例題が複数ある場合は、先に登場するものほど重要視してください。 次に、練習問題を。＊一つまででいいです。
余力があれば、同じ範囲を「風」についても！
苦手にしていない人にとっても、頻出項目は重視する必要があります。
※ ＜入試直前＞ はここまでです。
Q. 物理と地学を教えています。 河合塾から出版されている「私が選んだこの一冊」の中にある「地球の科学」の推薦文を生徒に読ませたいと思いますが、コピーを配布して構わないでしょうか？
A. もちろんです。多くの生徒さんに読んでもらいたいと思って書いたものですから、ありがたいと思います。 このホームページにも掲載することにしました。
書いた時点で（2013年）、既に本は絶版になっており、入手も難しい状態でした。 本そのものを読んでほしいというよりも、科学的思考法・探究法の一面が鮮やかに照らし出されている例として、推薦文を読んでもらうこと自体に意味があると思っていたものです。
力 学 //////////////////////////////////////////////////////////////////////////////////////////////
Q. 作用・反作用の力は 同種の力と思っていいでしょうか ？
「エッセンス」にある、２つの物体の万有引力とか、２つの帯電体の静電気力はそうなっています。 また、２つの物体が接触して押し合っているときの力はいずれも垂直抗力です。 さらに、床上の物体が床から摩擦力を受けるとき、床も力を受けますが、摩擦力です。
A. 作用・反作用は２つの物体間で働く力 ですね。 同じ大きさの力を 反対向きに及ぼし合います。 確かに同種の場合が多いのですが、そうでない場合もあります。
人が壁を押せば、壁から反作用を受けます。 反作用は垂直抗力で、人の力とは異なります。 糸とばねがつながれていると、糸がばねを引く力は張力Ｔで、ばねが糸を引く力は弾性力Ｆです。 もちろん、作用・反作用の法則から Ｔ＝Ｆ です。
関連して、ひとこと付け加えたいことがあります。
軽い糸の張力は両端で同じ です。 １本の糸のどこでも張力Ｔが同じなのです、加速度運動中であったとしても。 これは 作用・反作用ではなく、糸の質量が無視できることに依っています（「エッセンス(上)」p43)。 軽いばねの弾性力Ｆも同様です。
そこで、「軽い糸と軽いばねが結ばれていると、全体について 力 (張力と弾性力) が同じになるのです。 その力は ばねの伸びｘを用いて ｋｘ と表せる」ことになります。
（ｋ：ばね定数）
※ 手のひらの上に物体を置くと、物体は垂直抗力で支えられているとみなすこともできる。 手の力自体が垂直抗力の一種と考えることが可能である。 また、糸の張力の原因は 糸がわずかとはいえ引き伸ばされていることによる。 張力は弾性力の一種と考えてもよい。 力の原因をさかのぼって考えたとき、「作用・反作用の力はすべて同種」という主張は可能である。
垂直抗力、摩擦力、張力、弾性力などは すべて２物体の接触による力であり、物体の変形を戻そうとする力である。 分子・原子のミクロなレベルにまでさかのぼれば、電磁気力による力であり、電磁気力が作用・反作用を満たしていることが起因している。
Q 『Q＆A エッセンス』に、力の図示と運動方程式についての話の中で、次のような記述があります。 大筋は分かりますが、一か所 気になりました。
＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊
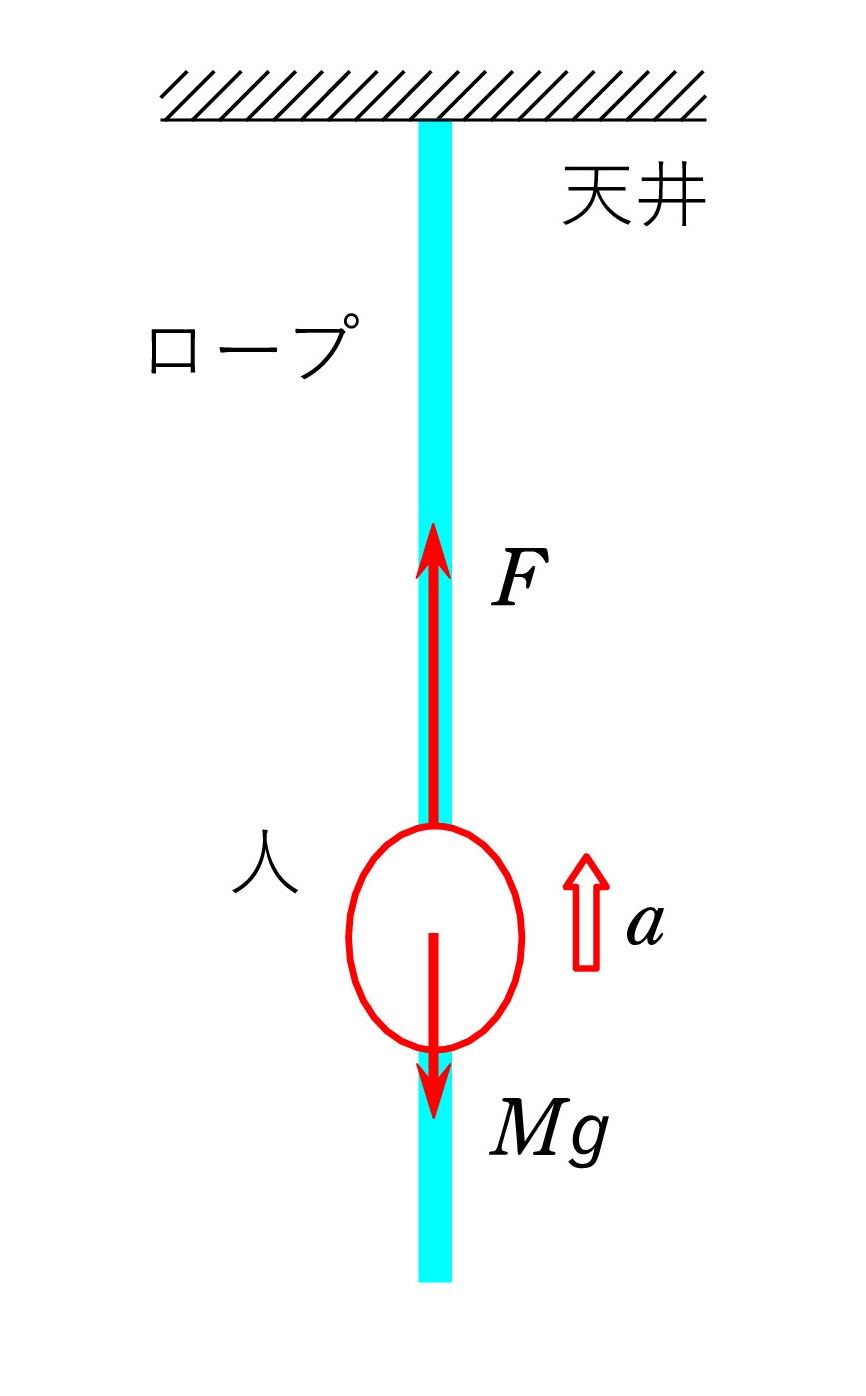たとえば、天井から垂らされた軽いロープを、質量Ｍの人が登っていくケースとします。 図示は人を丸か四角で表し、下向きの重力 Ｍｇ と上向きの力Ｆを描けば十分。 上向きの加速度を a とすると、運動方程式は Ｍa ＝ Ｆ−Ｍｇ ですね。なお、Ｆは張力です。 人はロープに下向きの力を加え、その反作用Ｆを上向きに受けるからというのが、ていねいな説明です。 でも、人も物体と思えば・・・ロープからの力は張力に他ならないはずです。 ロープが人を吊り下げている と考えてもいいのです。
＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊
「軽いロープ」となっていますが、質量のあるロープではまずいのでしょうか？
ロープ自体は静止しているので、問題ないと思いますが・・・
A. 確かに、人の運動方程式に変わりはありません。 しかし、「上向きの力 F は張力です」と言えなくなります。 ロープの張力が変わってきます。
ロープに質量があると、垂れ下がっているだけで、張力が発生しています。 ロープの任意の断面に注目すると、そこから下側の部分の重力分を支えているからです。 したがって、ロープの張力は上に行くほど増し、上端で最大になっていることも分かるでしょう。
人が登るときは、手の位置での張力は、手から下にあるロープの重力分に 人の力 F が加わったのを支えています。
分かったかどうか、次の問題でチェックしてみてください。
天井にかかる力の大きさがＳを超えると、ロープが外れるとします。
質量 Ｍ の人が登るときの加速度の最大値 amax はいくらでしょうか ？
ロープの質量を ｍ とし、人が静かにぶら下がっただけでは外れないとします。
解答（※）は最後に
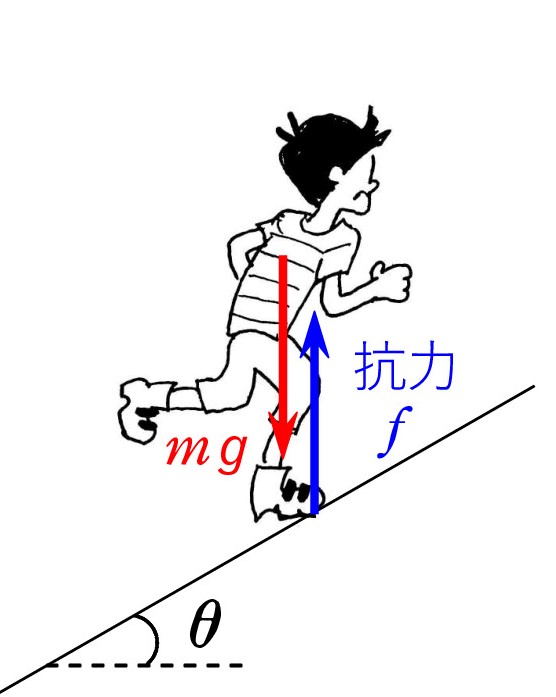
Q1. 子供が斜面を一定の速さで駆け上がっていきます。 子供の質量は ｍ、斜面の傾角は θ で、空気の影響を無視します。 「子供が斜面から受ける力の大きさ ｆ」が尋ねられ、 ｍｇｃｏｓθ と答えたら、× になりました。 納得がいきません。
A. 共通一次の問題ですね。 （ 共通一次 は センター試験 を経て 共通テスト に移行 ）要点は二つです。 まず、「等速度運動は力のつり合い 」であり、次に、斜面から受ける力は、垂直抗力ではなく、「抗力」だということです。 抗力とは 垂直抗力と摩擦力の 合力です。 もともと一つの力(抗力)を 垂直抗力Ｎ と 摩擦力Ｆ に分解して扱っているのです。 そうした方が理解しやすいからです。
子供に働く力は 重力 ｍｇ と 抗力 ｆ の２つであり、それらがつり合っているのですから、抗力は鉛直上向きであり、ｆ＝ ｍｇ です。
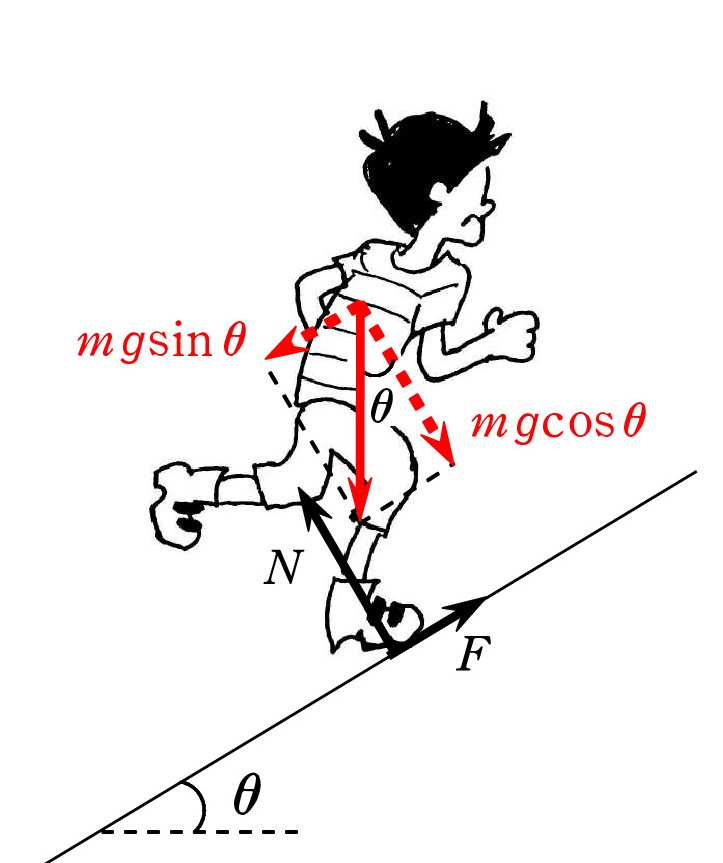斜面方向と垂直な方向に分解 して考えてもいいです。 というか、それが 斜面問題に対する鉄則 かもしれません。 垂直方向では、垂直抗力 Ｎ ＝ ｍｇｃｏｓθ （これがあなたの答えです)。 そして、斜面方向では、摩擦力 Ｆ ＝ ｍｇｓｉｎθ ですね。すると、 ｆ2 ＝ N2 ＋ F2
＝（ｍｇ)2（ｃｏｓ2 θ ＋ ｓｉｎ2 θ）＝（ｍｇ)2
よって、 ｆ ＝ ｍｇ
随分、回りくどいですね。 抗力の向きが鉛直になっていることにも 気づかないまま通り過ぎそうです。
鉄則がいつもベストとは限りません 。
Q2. 摩擦力 Ｆ が斜面方向上向きになっているのが不自然です。 子供は駆け上がり、摩擦は運動を邪魔するはずで、斜面方向下向きではないでしょうか？
A. そう思う人が多いですね。 動摩擦力なら動く向きと逆ですが、足は斜面に対して滑っていないので、Ｆは静止摩擦力であり、その向きは状況によります。
また、子供は 足で斜面を下向きに押すので、Ｆは下向きだと主張する人も出ます。
力のつり合いや運動方程式で考えているのは 注目物体が受けている力 です。 子供は 斜面を下に押すことによって、反作用Ｆを上向きに受けているのです。 人間が絡むと、つい、与えた力にとらわれがちです。 作用・反作用の法則 に要注意！
子供が斜面を降りるときも、等速度なら、力は全く同じであること にも注意してください。 言うまでもないことかもしれませんが、斜面上で止まっているときも 力は同じです。
Q3. 考えてみれば、ふだん地面を歩いているときも、静止摩擦ですね。 車の場合はどうなんでしょうか。
A. 自動車が進むときも同じで、駆動輪で地面を後ろ向きに押すことによって、前向きの推進力（実体は静止摩擦力）を得ています。駆動輪はエンジンにつながるタイヤです。車体の前進速度とタイヤの回転速度の合成のお陰で、地面との接触部の速度は０で、静止摩擦になります。
一方、駆動輪でない、転がるだけのタイヤでは、まさに自動車の運動が邪魔され、後ろ向きの摩擦力を受けています。
凍った路面や雪道での発進で、スリップするときは動摩擦になります。それでも駆動輪は前向きの力を受けて前進できます。タイヤが地面に対して後方に滑り、動摩擦を逆向きに、つまり、前方に受けるからです。しかし、静止摩擦に比べてずっと小さいので、動きが悪いのです。
ついでですが、走っている車を急ブレーキで止めるとき、タイヤの回転を止める（ロックする）と、スリップして小さな動摩擦でしか止められません。 タイヤが滑らないように回転させながら静止摩擦を利用した方が早く止められるので、急ブレーキを踏むと、ＡＢＳという装置が働き、スリップを軽減できるようになっています。
（ＡＢＳ：Ａnti-lock Break System 車体のスピンを防ぎ、ハンドルでのコントロールも維持できる）
Q4. 推進力については汽車や電車でも同じでしょうね。
A. 同じです。問題集などで、推進力が車体の機関部で前向きに出現し、車輪では後ろ向きの摩擦力になっている図を見かけることがあります。問題を解く上では困らないのですが、理解が浅いとしか言いようがありません。機関部によって車輪が回され、接触するレールからの反作用が推進力です。
機関車の車輪では前向きの推進力（静止摩擦力）、連結車両の車輪では後ろ向きの摩擦力ということですね。
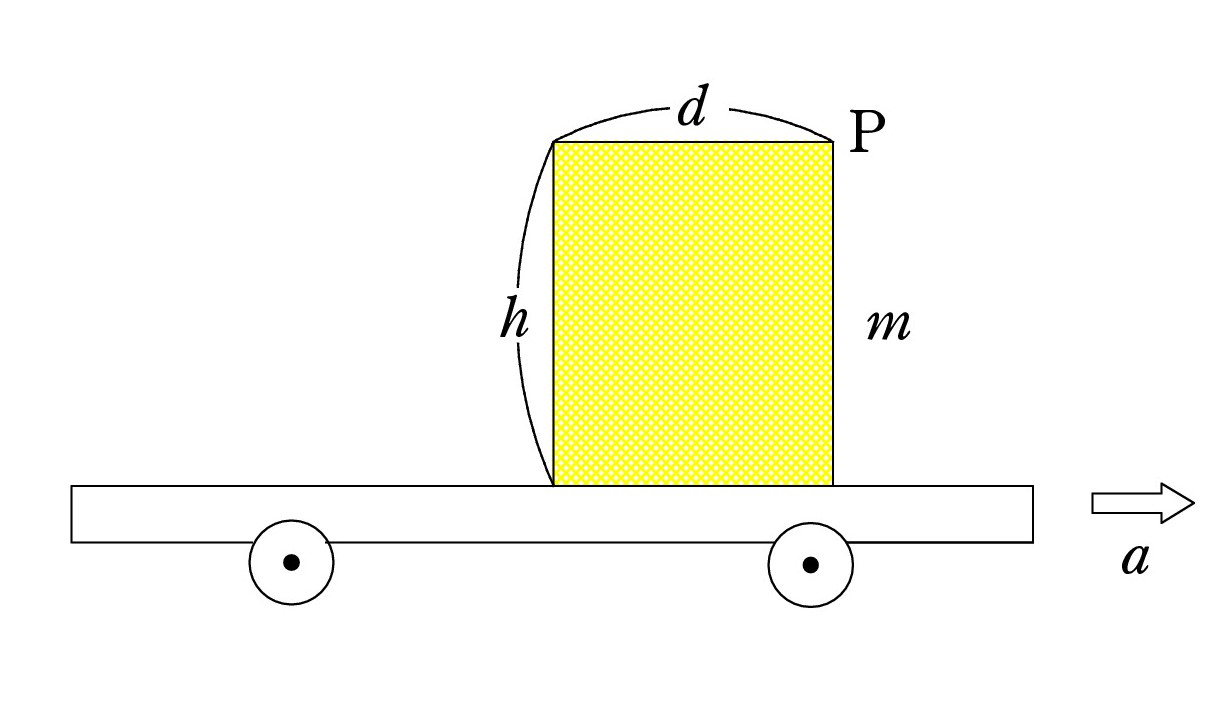Q1. 台車に力を加え、水平方向で加速度を徐々に増していきます。「台車上に置かれた、一様な直方体Ｐが倒れ始めるときの加速度を求めよ」という問題です。 質量 ｍ のＰは滑ることはなく、辺の長さはｈとｄです。やはり、慣性力で考えるのでしょうか。その場合、作用点はどこですか ？A. 動く台上での現象では慣性力が活躍します。 慣性力によって、自分の知っている世界（状況）での話に置き換えができる のです。
台車上の人にとっては、静止している物体が傾く普通の問題です。 ただ、加速度 α で運動している人ですから、慣性力 ｍα を考えなければいけません。 ｍα こそ倒す原因です。
そして、慣性力の作用点は Ｐの重心Ｇ になります。 Ｐを細かく分割し、それぞれに働く慣性力の合力の作用点を調べるのは、分割したそれぞれに働く重力の合力を考えることと同等だからです。微小部分（質量凾香jに働く 凾香Eα が 凾香Eｇ に対応しています。もちろん、微小部分に働く力はすべて同じ向きであることも共通です。
これで、典型問題になります（例えば「エッセンス」の力学の問題33)。
Q2. 先ほどの件ですが、慣性力で計算してみました。でも、結果に自信が持てません。 解答までお願いできないでしょうか。
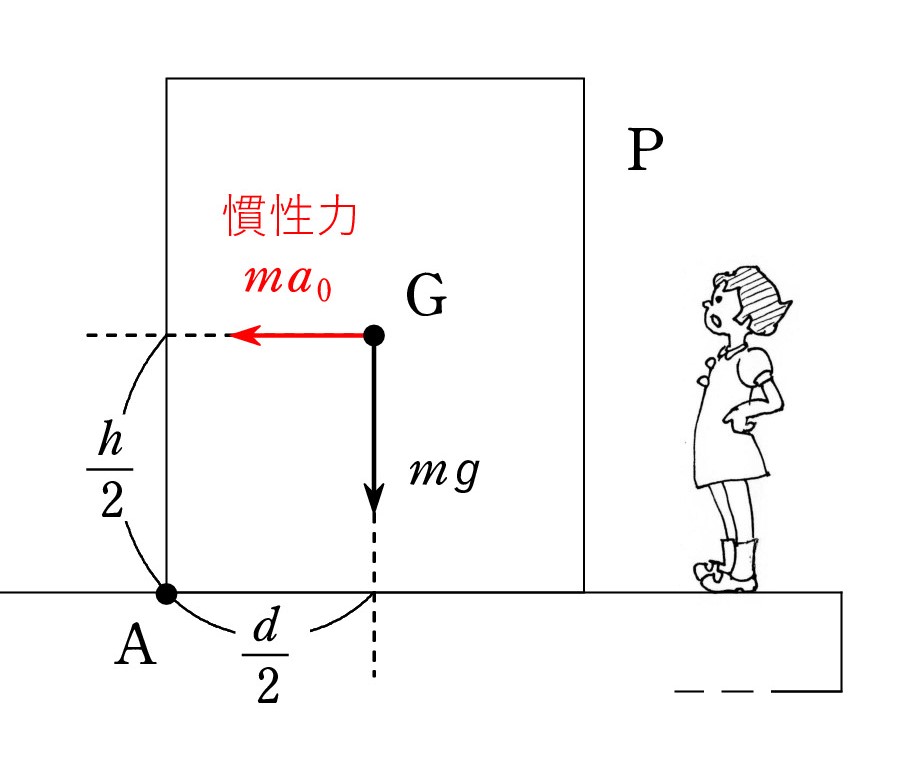A. Ｐ が傾く直前には、台車との接触は 事実上 左下の辺 Ａ になっている ので、Ａのまわりのモーメントつり合いより、加速度を α0 として、ｍα0 ・ｈ/２ ＝ ｍｇ・ｄ/2 ∴ α0 ＝（d/h)ｇ
モーメントのつり合いでは、すべての力が参加する のですが、垂直抗力 Ｎ と静止摩擦力 Ｆ の作用点は Ａ なので、モーメントがないことを踏まえています。
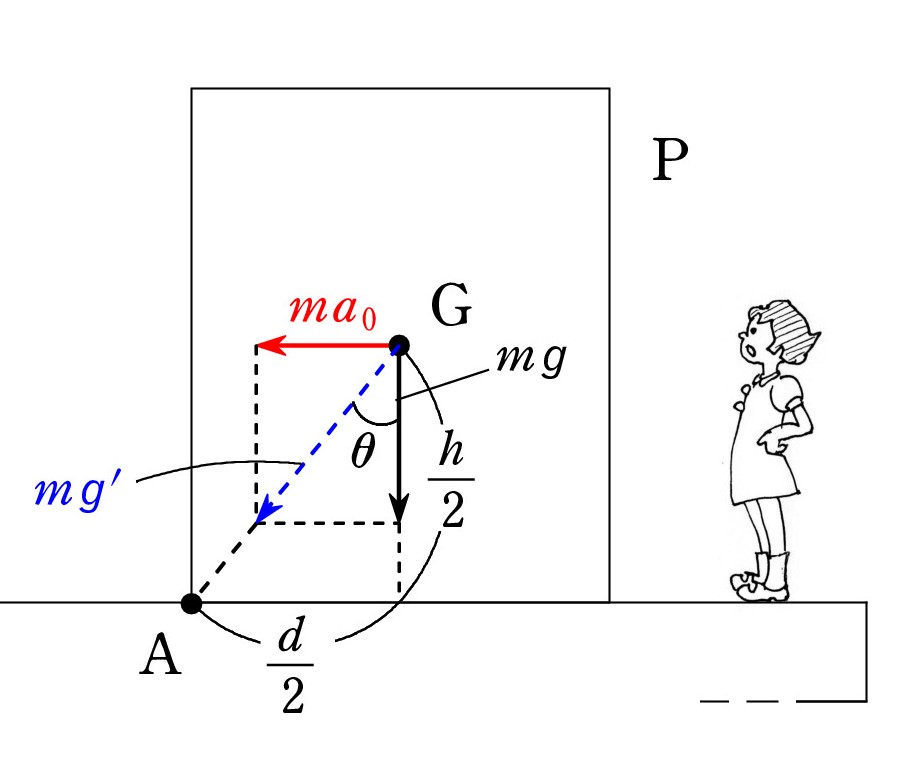別の方法もあります。 Ａに注目するのは同じですが、重力と慣性力の合力のモーメントが０になればよいので、合力（青矢印）は Ａを指すはずです。あるいは、合力を見かけの重力 ｍｇ‘ と考えれば、Ａが「真下の点」になったとき とみることもできます。
これらの場合は tan θ ＝ (d/2) / (h/2) ＝ ｍα0 /ｍｇ として求めます。
では、ここで問題です。３問あります。
(1) Ｐが倒れ始めるときの台車を動かす力Ｆ0 を求めよ。質量Ｍの台車は滑らかな水平面上を動くとする。
(2) Ｐが滑ることなく、倒れるための、Ｐと台車の間の静止摩擦係数 μ に対する条件を示せ。
(3) α＜α0 のとき、垂直抗力の作用点はどこになるか、25 字以内で述べよ。
ヒント：摩擦のある斜面上に置かれた物体の場合を思い出す（エッセンス（上）ｐ31）。
解答（※※）は最後に
Q3. 答えの α0 ＝（d/h)ｇ を見ると、Ｐの質量 ｍ が含まれていません。 答えに自信が持てなかったのはそのせいです。必要のない ｍ を与えたのは出題者の意地悪でしょうか。
A. そうとも言えません。 ｍ は考えを進めるのに役立っています。 逆に言えば、問題文に登場しない量でも、考察に必要なものは自分で用意していく姿勢が大切 です。
答えが ｍ によらないのは 「フーン」と感心してほしい特徴です。 重くても軽くても関係ないというのは、見かけの重力の観点なら「なるほど」と理解できます。
また、ｄが小さく、ｈが大きいほど α0 が小さいという結果は、物体の倒れやすさの実体験からも納得がいくでしょう。 このような 答えの吟味は大切 です。
答えから、Ｐの大きさではなく、ｄ/ｈ という比で決まること、Ｐの奥行きは関係ないことなどが分かります。（ 意地悪な出題者なら、奥行きを与えます。）
また、導き方をたどると、直方体でなく、円柱でも同じですね。ｄは直径になります。
以上のような考察をしていると、いろいろと試してみたくなります。
お盆の上に 様々な直方体や円柱を置いて、机の上で水平に揺すり、振動を激しくしていけばよいでしょう。どれから倒れるか、同時に倒れるのはどれとどれかなど、予想しながらやれば、興味が尽きないでしょう。
一様な直方体や円柱が身近になければ、やはり、導き方からして、中が空洞の箱でもよいことが分かります。重心位置に変わりはないからです。紙パックや缶の飲み物が利用できます（中身 有りと無しで）。
直方体ならどの２辺を用いるかとか、アルミ缶のように滑りやすいものには底に紙を張るとか、工夫してみてください。お盆より厚手の新聞紙が扱いやすいかもしれません。
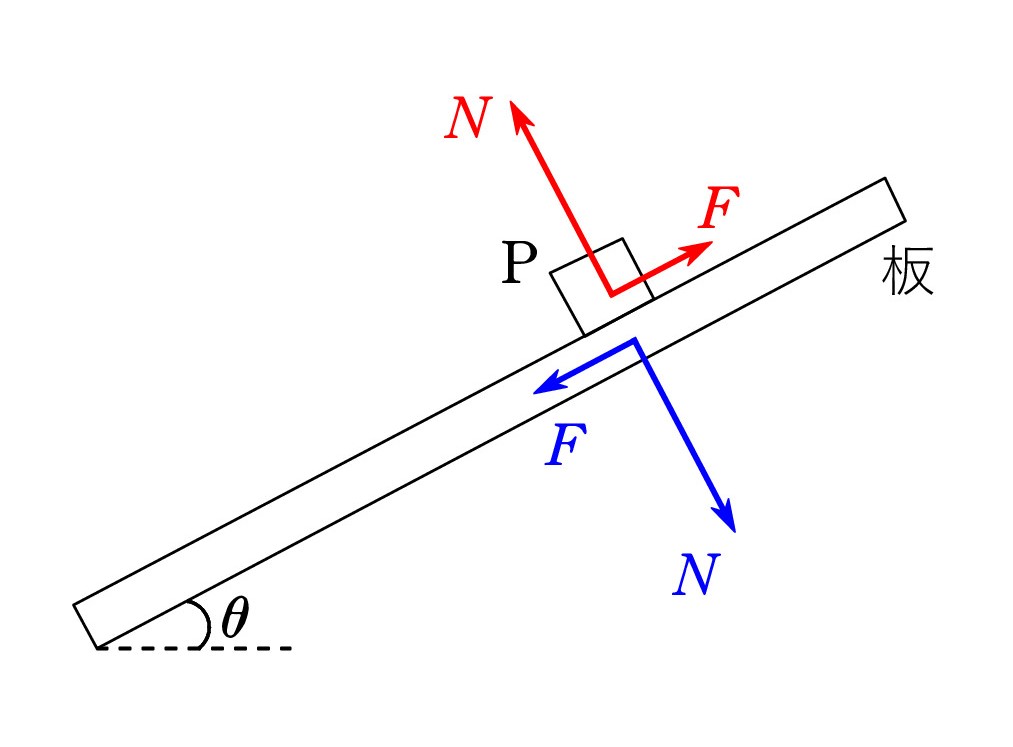Q1. 質量Ｍの板が水平から角度 θ 傾いて静止しています。 周りの状況はカットしました。糸でつり下げられていたり、壁に立てかけられていたり、いろいろです。 板上には質量 ｍ の小物体 Ｐ が置かれています。板について、力のモーメントのつり合い式を立てたいのですが、Ｐから受ける力が悩ましいのです。
板はＰを赤で示した垂直抗力Ｎと静止摩擦力Ｆで支えているので、板はそれらの反作用を受けるはずです。 青で示した反作用ＮとＦのモーメントを考えて解いていけばよいと考えたのですが、どうでしょうか？
Ｐの力のつり合いから、Ｎ ＝ ｍｇｃｏｓθ で、Ｆ ＝ ｍｇｓｉｎθ です。
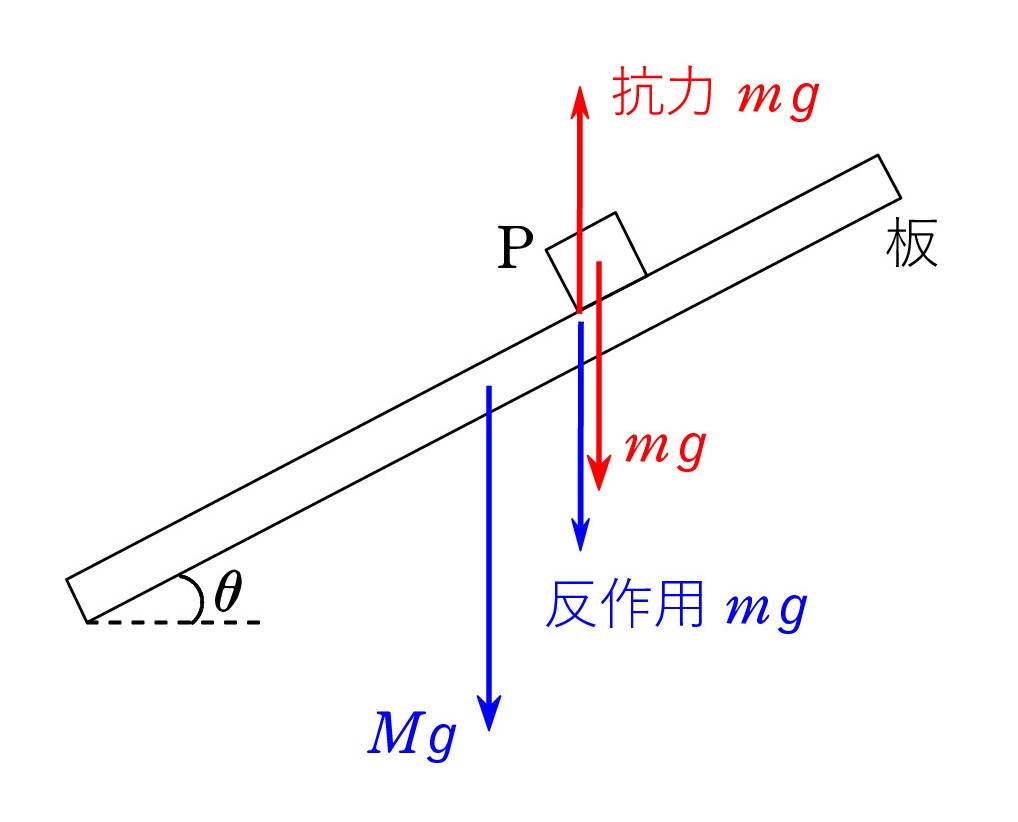A. 正しい方法です。 正統的と言ってもよいかもしれません。ただ、もっと簡単にすます手があります。 板はＰを鉛直上向きの ｍｇの力（抗力）で支えています。したがって、Ｐから鉛直下向きに反作用 ｍｇ（青）を受けています。
この一つの力でモーメントを計算できるのです。 Ｎ や Ｆ の確認も要りません。
初めから、鉛直下向きの ｍｇ を考えていた人もいると思いますが、重力と誤認していないでしょうか？ そうであれば、「結果オーライ」なだけで、重大な誤りです。
これからは「重力分がまともに板にかかるから」とワンクッション置いてほしいですね。
Q2. 板とＰを一体にすれば、重力は（Ｍ＋ｍ)g となり、両者の間で働く力は気にしなくてよくなるのではないでしょうか？
A. よいアイデアです。 力学に限らず、一般に「広くとらえる」見方が 物理では活躍 します。 ただ、モーメントの場合は 作用点が大事で、（Ｍ＋ｍ)g とするには、全体の重心を調べる手間がかかるのが 難点です。
そこで、「一体として扱うものの、重力については 板の Ｍｇ とＰ の ｍｇ とは 分けたままにしておく 」という 知恵 があります。 合力にしなければよいのです。 重力の矢印２本をそのまま生かすのです。 変則的ですが、モーメントでは 有力な方法でしょう。
Q3. いずれにしろ、P が板上で静止していることが要（かなめ）のようです。
もし、Ｐが板上で滑っていれば、板が受ける力は ｍｇ（青矢印）ではなくなるのですね。 板は静止しているとします。
A. そうです。 まさに、斜面方向とそれに垂直な方向に分解 して考える必要が生じます。
もし、板に摩擦がないと、板がＰに及ぼす力は 垂直抗力 Ｎ ＝ ｍｇｃｏｓθ だけであり、その反作用を用意すればいいのです。
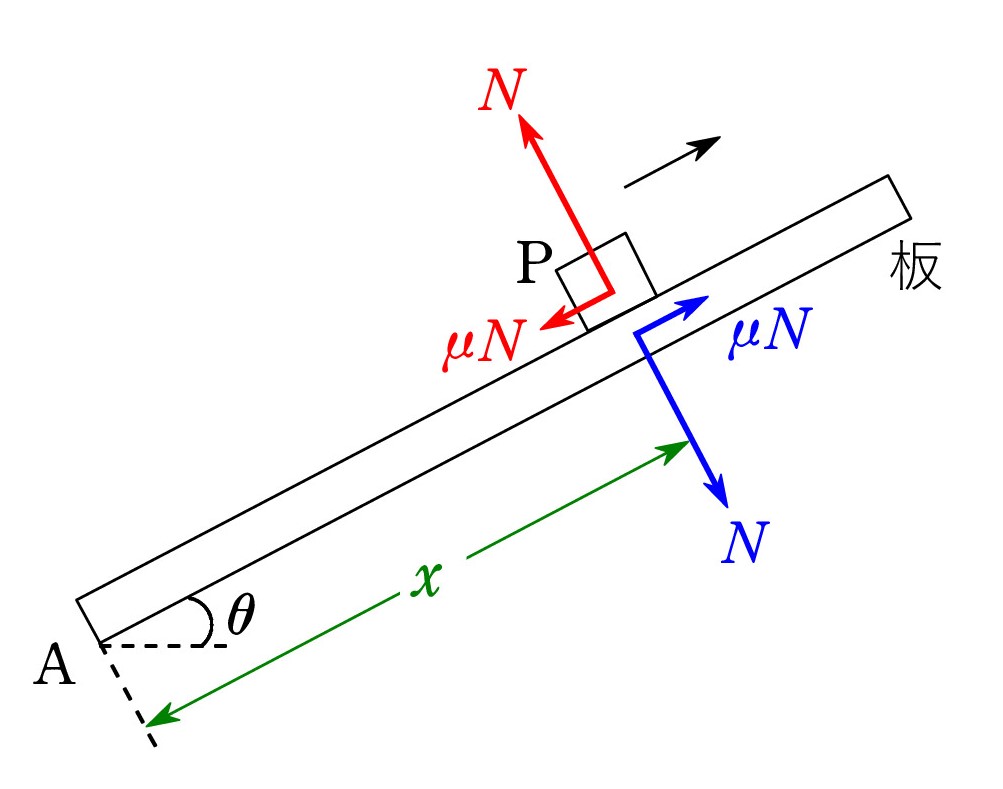摩擦があれば、Ｎの反作用に加えて、動摩擦力 μＮ の反作用を用意しなければなりません（ μ：動摩擦係数 ）。モーメントのつり合い式では、回転軸はどこにとってもよい ので、板の端を選ぶとよいでしょう。 後者（μＮ）のモーメントはなく、前者（Ｎ）のモーメントの計算も たいしたことはありません。
図はＰが上へ滑る場合です。Ａを軸の位置とし、ＡＰ ＝ ｘ とすると、モーメントは 時計回りに Ｎｘ（＝ｍｇｘｃｏｓθ）です。
Ｐが上に行くほど大きくなっていくことにも注意してください。 板が壁に立てかけられている場合、板が滑り出すという問題につながります。
Q1. 糸で結ばれた２物体があり、糸が滑らかな滑車にかけられ、２物体が運動します。 運動方程式で解けるのですが、力学的エネルギー保存則で解いてみようと思いました。
全体（物体系）に対して式を立てる必要がある ことは理解しています。 重力の位置エネルギーの基準ですが、両者共通の位置（高さ）にするのが面倒なので、物体ごとに基準を決めてもいいでしょうか。
A. 物体ごとでも O K です。 負の位置エネルギーを避けるように、基準位置は下の方にとるとよいでしょう。
ただ、基準位置を気にしないですむ方法があります。エネルギーの全量ではなく、増減に注目するとよいのです。（失われたエネルギー）=（現れたエネルギー）と立式します。（減少分）=（増加分） と言ってもいいです。
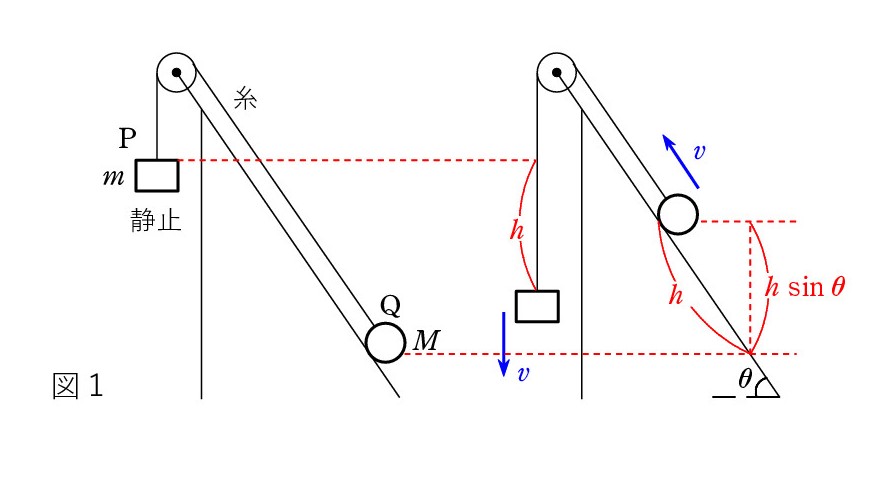
たとえば、図１のようなケースで、質量 ｍ の P が下がって、滑らかな斜面上の質量 M の Q を引き上げるとします。静止状態から P が ｈ 下がったときの速さを ｖ とすると、
ｍｇｈ ＝ ｍｖ2/２ ＋ Mｖ2/２ ＋ Mｇ・ｈsinθ
人によっては、P と Q の位置エネルギーの実質的な減少分は ｍｇｈ− Mｇ・ｈsinθ で、これが２つの運動エネルギーに変わると考えます。それも立派な見方です。
Q2. 上の図１で、P が下がるための条件を考えてみました。
上がるか下がるかの境目が力のつり合いなので、そのときの糸の張力を T とすると、P について T ＝ ｍｇ、 Q について T ＝ Mｇsinθ なので、 ｍｇ ＝ Mｇ sinθ です。 P が下がるためには ｍｇ＞ Mｇ sinθ よって、 ｍ ＞ M sinθ が条件と思います。これでよいでしょうか。
A. 正しいです。 ただ、もっと楽に考えることができます。図２のように １次元化してみると、分かりやすい でしょう。糸方向の力の成分を取り出しています。そして、P と糸と Q 全体に注目しているので、張力は顔を出しません。 ｍｇ＞ Mｇsinθ は一目瞭然でしょう。
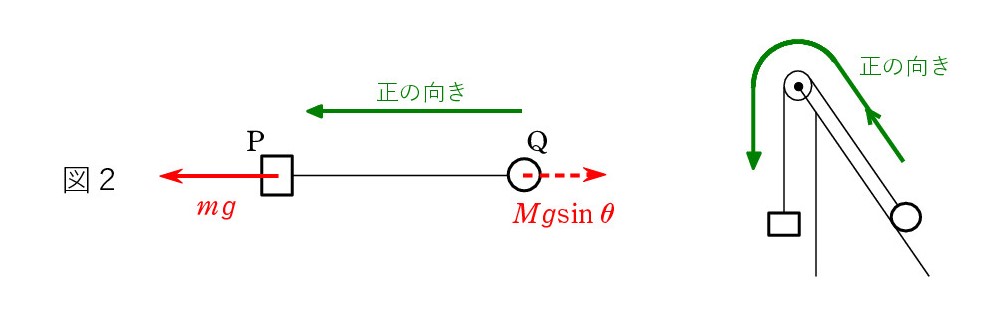
この見方が優れているのは、運動に対しても適用できることです。P が落下する加速度を a とすると、図２では左向きを正として a であり、全体に対しての運動方程式は、
（ｍ ＋ M）a ＝ ｍｇ−Mｇsinθ
アッという間に加速度 a が決まります。暗算でもできるかも。
図１だと、a と張力 T を未知数として、P と Q それぞれに対しての運動方程式を立て、連立で解くというのが通常の方法ですが、それに比べて格段に早く求まります。斜面に摩擦があってもできます。 「１次元化」＋「一体化」のコンビネーションの威力！
ひとこと。 P と Q を別々で扱う通常の方法でも、加速度 a に符号を含めるときには、右端の図のように「正の向き」につながりをもたせる必要があります(逆向きが正でもOK )。 今まで何となくやってきた人が多いと思いますが。
もうひとこと。 もし、張力 T まで知りたいのなら、１次元化 ＋ 一体化 で a を求めた後、P か Q のどちらかに注目すればよいのです。 P なら ｍ a ＝ ｍ ｇ − T として。
一体で解き、部分に移るのが賢明 です。 力のつり合いでもそうです。
運動方程式や力のつり合いに限らず、対象を広くとらえることによって、重要な情報をまず把握し、必要に応じて部分に目を移し、詳細に調べていくのが 賢者の道 です。
Q. 宇宙ステーションでは無重力で物が浮いていますね。地表から ｈ ＝ 400 km ぐらいの高さを回っているとのことですが、それだけ離れると万有引力が事実上なくなってしまうということでしょうか。
A. とんでもない誤解です。万有引力はしっかりあります。宇宙ステーション内で見れば、物体には遠心力が働き、万有引力とつり合っている ので、物体は浮いているだけです。「無重力状態」と言った方がいいでしょう。地球の半径は R ＝ 6400 kｍ あるので、宇宙ステーションは地球の表面スレスレを回っているようなものです・・・宇宙から見れば。
物体にはたらく万有引力は地表にあるときより弱くなっているのは確かです。どれくらいになっていますか？
・・・・・・・・？・・・？・・・？・・・？・・・？・・・・・・・・
GMｍ / (R＋h)2 ÷ GMｍ / R2 ＝ R2 / (R＋ｈ)2
＝｛6400 / (6400＋400)｝2
＝ （16 / 17)2 ＝ 0.88… 約 90％ ですね。
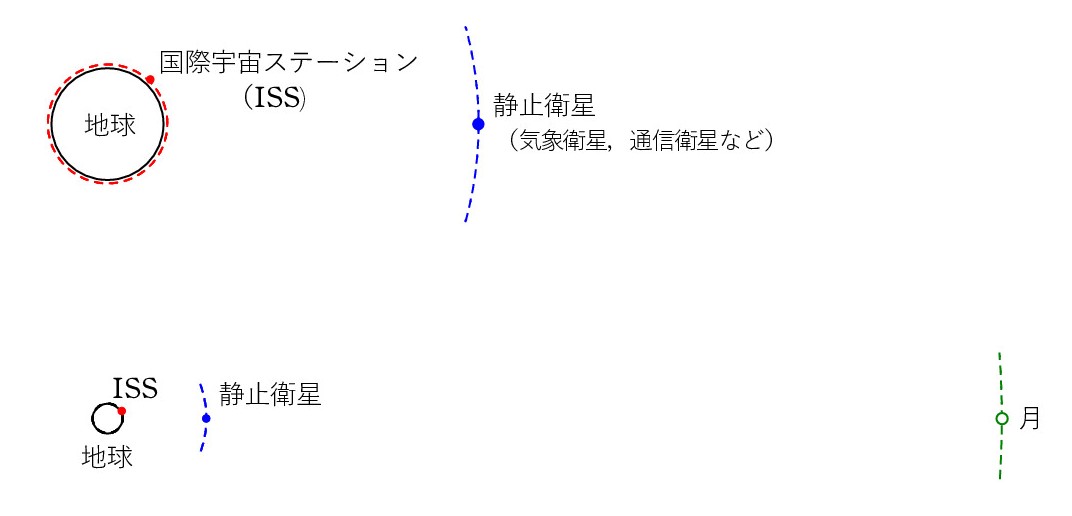
一口に人工衛星と言っても、ISS は驚くほど近く（これで大気圏外！）、静止衛星は意外に遠い。
回転周期 T は ISS が 90分、静止衛星は １日（当然！）、月は 27日。
さて、 これらの数値と関係があるのは上図の何 ？ （解答 ※※※ は最後に）
回転周期 T は ISS が 90分、静止衛星は １日（当然！）、月は 27日。
さて、 これらの数値と関係があるのは上図の何 ？ （解答 ※※※ は最後に）
熱 //////////////////////////////////////////////////////////////////////////////////////////////
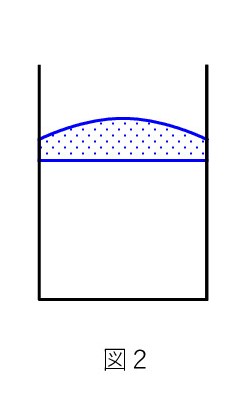
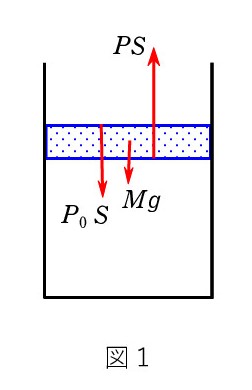
Q. 熱力学で、容器内の気体の圧力 Ｐ を決めるのに、滑らかに動くピストンのつり合いを利用する場合、図１なら、
ＰＳ ＝ Ｐ0Ｓ ＋ Ｍｇ は分かります。 Ｐ0 は大気圧、Ｍ はピストンの質量、Ｓ は容器の断面積です。
図２の場合も大気の力は Ｐ0Ｓ でいいのでしょうか ？
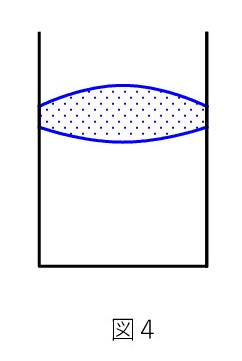
A. 大気の力の鉛直成分は Ｐ0Ｓ です。 まず、図３の場合で確かめてみます。大気圧は面に垂直にかかる ので、上面の面積を Ｓ‘ とすると、大気の力は Ｐ0Ｓ‘ で斜め方向です。ところが、鉛直方向の成分は点線矢印で、Ｐ0Ｓ’ｃｏｓθ であり、これは Ｐ0S に等しいのです。 Ｓ‘ｃｏｓθ ＝ Ｓ だからです。
「面積の ｃｏｓ？」と思うかもしれませんが、 容器の断面が長方形なら、 辺の ｃｏｓ と同じです（奥行きは図１と同じなので）。
長方形でなくても面積の ｃｏｓ でいいことは知っておくとよいでしょう。
図３が Ｐ0Ｓ でいいのなら、図２も微小部分に分割すれば、斜面の寄せ集めであり、同じことです。
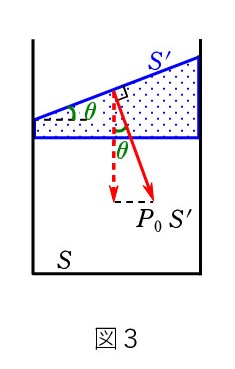
なお、下面も水平である必要はなく、図４でも ＰＳ ＝ Ｐ0Ｓ ＋ Ｍｇ です。
要するに、重要な量はピストンの形ではなく、断面積 Ｓ ですね。 容器の断面積 Ｓ と言った方がいいでしょう。
Q. 単原子分子からなる理想気体の内部エネルギーは Ｕ ＝ 3/2・ｎＲＴ と表されます。 学校の先生からは Ｕ ＝ 3/2・ＰＶ も大切だと言われました。 両方覚えた方がいいでしょうか ？
A. Ｕ ＝ 3/2・ｎＲＴ を優先させてください。 Ｕ が Ｔ で決まる（Ｔ に比例する）ことが最も大切 です。 確かに、状態方程式 ＰＶ ＝ ｎＲＴ により、 Ｕ ＝ 3/2・ＰＶ とも表せます。
ＰＶ グラフを扱うときなど大変便利な形です。 でも、「便利」に過ぎません。 Ｕ が 圧力 Ｐ や体積 Ｖ に依存するかのように見えるのが嫌なのです。
定圧変化での熱量 Ｑ の計算では、Ｑ ＝ ｎＣP 凾s が用いられます。
単原子なら、ＣP ＝ 5/2・Ｒ であり、
Ｑ ＝ 5/2・ｎＲ(Ｔ2−Ｔ1) ＝ 5/2・(ｎＲＴ2−ｎＲＴ1)
としてみると、 ここでも ｎＲＴ を ＰＶ に置き換えれば、Ｑ ＝ 5/2・(Ｐ2Ｖ2−Ｐ1Ｖ1）とでき、ＰＶ グラフ などで計算が速いです。 前の状態が１で、後が２です。
熱力学での は、変化であり、いつも「後−前」の順番です。
定積変化での Ｑ ＝ ｎＣV 凾s の計算についても同様です。
結局、「ｎＲＴ は ＰＶ に置き換えられる」と意識していること、いつでも活用できること が何よりでしょう。
New Q1. 「エッセンス」には、内部エネルギーの変化に対して、 儷 ＝ n CV 儺 が公式として掲げられています。 定積モル比熱 CV が含まれるのに、この公式は定圧変化にも使える、いやそれどころか、任意の変化に対して適用可能というのが、しっくりきません。
A. 内部エネルギー U は絶対温度 T に比例する ので、同じ温度変化 儺 なら どのような変化であれ、内部エネルギー変化 儷 は同じになります（ y ＝ a x なら 凾 ＝ a 凅 a：定数 )。
そこで、定積変化に目を向けると、仕事 W が０なので、吸収熱量を Q として、第１法則は 儷 ＝ Q ＋０ 一方、定積では Q ＝ n CV 儺 したがって、 儷 ＝ n CV 儺 定積で調べたこの結果は 任意の変化に適用できる・・・というわけです。
New Q2. U ＝ a T であり、儷 ＝ a儺 そして、定数 a を定めるには、定積変化を利用すればよいということですね。 数学的には 分かるんですが・・・
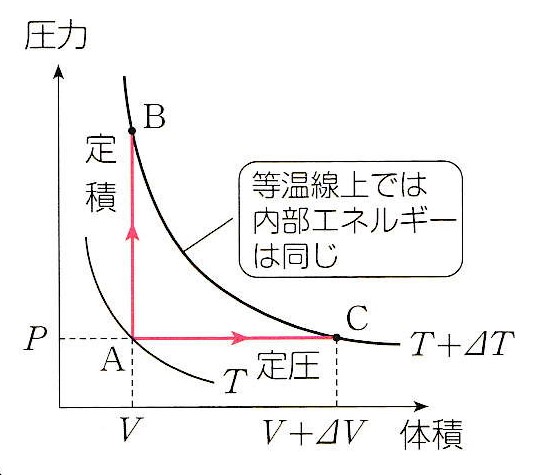A. では、もう少し物理らしくしてみます。温度 T の状態 A から温度を 儺 だけ上げるとします。 定積でも 定圧でも いろいろな変化で上げられます。
P V 図上では T ＋ 儺 の状態は一つの等温線上にあります。それらは内部エネルギーが同じ状態であることに注意してください。
すると、状態 A からの内部エネルギーの増加 儷 は、定積変化 A → B で測ったものに等しいことになるでしょ。 等温曲線 T ＋ 儺 上のどの位置 X に達していたとしても です。 A → X 間が直線である必要もありません。
「 温度が同じなら内部エネルギーは同じ 」ということがキーポイント。
温度は 分子の(平均の)運動エネルギーで決まり、理想気体の内部エネルギーは分子の運動エネルギーの総和だからです。
定積に対する Q ＝ n CV 儺 と、任意の変化に対する 儷 ＝ n CV 儺 はしっかり区別してほしいですね。
Q1. 気体が状態 A から B までは熱量 Q1 を吸収し、状態 B から C までは熱量 Q2 を放出しています。「 A から C までに吸収した熱量はいくらか」と問われました。
Q1 と答えるべきでしょうか ？ それとも、Q1 − Q2 でしょうか ？
A. Q1 − Q2 です。 「差し引きの吸収熱量」が問われていると判断します。
A から B までの吸収熱量は Q1 で、 B から C までの吸収熱量は −Q2 だから、その合計と考えてもいいでしょう。
Q1 と答えさせたい場合には、出題者は「真に吸収した熱量」とか「高熱源から得た熱量」のように断ります。断りがなければ、「差し引きの」熱量です。「正味の」とか「実質の」と表現されることもあります。
文意から判断できる場合もあります。「A から C までの間で吸収した熱量と放出した熱量は それぞれいくらか」なら、吸収が Q1 で、放出が Q2 と答えます。
＊ 質問のケースのように、吸熱と放熱の切り換わりが明らかな場合、出題者は Q1 − Q2 を答えさせたいのなら、紛らわしさを避けるため、「差し引き」であることを断るべき とは思います。
Q2. 仕事も同様でしょうか？
A. 同様です。 ある過程の間に W1 の仕事をされ、 W2 の仕事をしたとき、「された仕事は？」と問われれば、 W1 − W2 と答え、「した仕事は？」なら、−W1 ＋ W2 と答えます。
そもそも、熱力学 第1法則 儷 ＝ Q ＋ W において、Q は「吸収した熱量」、W は「された仕事」と表現されますが、いずれも「差し引き」を意味しています。熱力学では断りがなければ、「差し引き」です。
第１法則を用いて 儷 と W から Q を求めた場合も、Q は差し引きです。 ただ、熱の吸収(あるいは放出)が続いているケースがふつうです。
たとえば、熱効率 e の場合は、次のようにきちんと断っています。
１サイクルについて、 e ＝（実質的にした仕事）/（真に吸収した熱量）
Q3. 熱量と仕事は「差し引き」と分かりました。 内部エネルギーもそうでしょうか？
A. 内部エネルギー U は気体の状態で定まる量です。 第１法則の 儷 はその「変化」であり、（後の U ）−（前の U ）です。 途中の増減は関係ありません。
あえて途中の増減が知りたければ、内部エネルギー U は絶対温度 T に比例する ので、温度の増減を確かめてから計算に入ることになります。
Q4. 儷 も「差し引き」には違いないように思えますが・・・
A. 結果的にはそうですが、「差し引き」という認識は希薄です。 内部エネルギー U は熱量 Q や仕事 W とは一線を画しています。
第１法則は ある状態 A から状態 B に変化する際のエネルギーの出入りを扱っています。 A から B への変化の過程にはいろいろなものがあり、熱量 Q と仕事 W は過程によって変わりますが、 内部エネルギーの変化 儷 は過程に関係しないという認識が大切です。
儷 ＝ Q ＋ W は、（後の U ）＝（前の U ）＋ Q ＋ W とした方が理解しやすいかもしれません。 Q と W が流入したエネルギーを表しています。 ていねいに言えば、正の場合が流入、負の場合が流出です。
Q5. エネルギーである U と、エネルギーの出入りを表す Q や W との違いを意識せよということですね。
A. その通りです。 エネルギーの方が格が上の量です。 Q と W は同格の量です。
力学では仕事 W しか現れませんが、同様です。 仕事よりエネルギーが格上です。
そして、運動エネルギーの変化が仕事に等しいのでした (仕事＝運動エネルギーの変化)。
熱力学第１法則と類似しています。
Q 断熱変化で、ＰＶγ ＝ 一定 は公式として用いてよいでしょうか？ 教科書によって扱いが違うようですが…。
A. 微妙な公式です。 断熱変化では ＰＶγ ＝ 一定 の他に ＴＶγ−1 ＝ 一定 もあります。 現在のところ、用いる場合は問題文で提示する大学が殆どです。
提示がないとすると・・・まず、状態方程式（または ボイル・シャルルの法則）で解けないか、次に、熱力学第１法則までで解決できないか 考えます。 それでもだめな場合に用いることになります。
比熱比 γ は γ＝ＣP/ＣV で、単原子気体の場合には、ＣP＝5/2・Ｒ、ＣV＝3/2・Ｒ なので、γ＝5/3 に置き換えができるように。
ＰＶγ ＝ 一定 と ＴＶγ−1 ＝ 一定 は同値です。 ＰＶγ＝ＰＶ・Ｖγ−1＝ｎＲＴ・Ｖγ−1 と、状態方程式を用いて変形してみると、ｎＲ が一定であることから分かります。 言うまでもないことですが、２つの公式の一定値は異なります。
γ か γ−１ か紛らわしいので、ＰＶγ ＝ 一定 を優先させて覚えてください。
波 動 //////////////////////////////////////////////////////////////////////////////////////////////
Q. ドップラー効果で振動数を問われるのは公式で処理できるのですが、波長を問われると、どうしていいか分からなくなってしまいます。
A. 振動数の公式は、音源が動く場合に波長がどうなるかを考えて導いたものです。まず、そこをしっかり復習してください。音源が動くから波長が変わる のです。
このとき、音速は音源の速度によらないことが本質的に重要です。観測者の動きは波長には関係ありません。反射板も音源の役割をするので、板が動けば波長を変えます。
ただ、実戦的な方法も知っておくといいでしょう。 観測者にとっての振動数 ｆ が公式で分かった段階からなら、 ｖ ＝ ｆ λ から波長 λ は求まります。 ただし、ｖ としては、観測者にとっての音速を用いること。音速 V は地面に対しては一定ですが、動く観測者にとっては、相対速度で速くなったり遅くなったりしています。 ｖ と ｆ と λ はすべて観測者が測った値にしなければなりません。ただ、λ は観測者によらない のです。
静止している観測者を自分で用意して、振動数 f1 を公式で求め、V ＝ f１ λ として、 λ を求めてもいいです。
Q1. ドップラー効果の入試問題で、音源の速さｖと観測者の速さ u が音速Ｖより十分小さい（ｖ≪Ｖ、u ≪Ｖ）となっています。 ドップラー効果の公式を用いる際の条件は、単に ｖや u が 音速より小さい（ｖ＜Ｖ 、u ＜Ｖ）ではないのでしょうか？
A. そうです。 条件は「音源や観測者の速さが音速より小さい」ことで、「十分に小さい」必要はありません。 そのように誤解している人もいますが。
ｖ≪Ｖ 、u ≪Ｖ は その問題での特別な制限です。 おそらく、うなりを扱う問題だと思います。 ドップラー効果では うなりがよく問題になります。
１秒間のうなりの回数(振動数)ｎは、２つの音波の振動数の差に等しく、 ｎ＝|f1−f2| です。 このとき、f1 ≒ f2 であることが必要ですが、ｖ、u が十分小さければ 大丈夫です。
もう一つの目的は、というより 最大の目的は、近似式を用いて簡略化できるということです。 たとえば、音源の振動数を f0 として、
f1 ＝f0 (Ｖ−u)/(Ｖ−ｖ) ＝ f0 (１−u/Ｖ)(１−v/Ｖ)-1
≒ f0 (１−u/Ｖ)(１＋v/Ｖ) ≒ f0 {１＋(ｖ−u)/Ｖ}
最後では、２次の微小量 (u/V)×(v/V) を無視しています。 f2 も同様に近似します。
ｎまでは正確に求め、その後に 近似するかもしれません。
とくに、数値計算では 近似して計算を楽にしたいということがよくあります。
|ｘ|≪１ のとき、 （１＋ｘ)n ≒ １＋ｎｘ は よく用いる近似式で、近似では、１次の微小量があれば、２次以下は無視 します。
Q2. ｖ≪Ｖ のような二重の不等式が与えられたら、近似しなければならないということでしょうか。
A. 必ずそうだというわけではありません。 近似なしの正確な表現も、複雑な表現になるでしょうが、認められると思います。
出題者は近似を促すか、答えの文字指定により、近似に導くのがふつうです。
正確な表記と近似した表記のどちらを書くべきか、迷った場合には、両方を書く手があります。
一方にしなければならないのなら、二重の不等式がある以上、近似した方にします。
Q3. 近似するとき、「１＋微小量」の形でなく、そのまま計算してはダメでしょうか。 たとえば、ｖ≪Ｖ、u ≪Ｖ のときで、ドップラーとは限らないと思ってください。
（Ｖ−u)(Ｖ−v） を V2−(u＋v)V＋uv とし、uv の項を落として、 V2−(u＋v)V としてはいけないのでしょうか。
A. それもＯＫです。
ただ、なぜ「１＋微小量」の形が 重視されるのかは 意識してください。 ある量が微小であるかどうかは他の量との比較の上でしか言えないのです。 たとえば、0.01 mm は微小だと思いますか？・・・10 μｍ と書けば そうは思えないのでは…
比較する相手は次元が同じ、つまり、単位が同じ量です。 今の場合、u /Ｖ や ｖ/Ｖ が微小なので、次のように計算すれば本格的です。
（Ｖ−u)(Ｖ−v） ＝ V2(１−u /Ｖ)(１−ｖ/Ｖ) ≒ V2{１−(u ＋ｖ)/Ｖ}
u /Ｖ や ｖ/Ｖ は無次元で、単位によらず同じ数値になることに注意してください。
たとえば、 u /Ｖ ＝ 0.01 なら微小量です。 正確には１に対してなので、「１＋微小量」というわけです。
ただ、質問のような計算法の方が早いという利点があります。 uv の項を無視するとき、そばに V2 があるからと思ってくれると万全です。
Q4. 熱力学の計算でも出合った覚えがあります。
A. いろいろありますが、理想気体の状態方程式の場合で見てみましょうか。
ＰＶ ＝ ｎRＴ ・・・@
P、V、T が微小変化すると、（Ｐ＋凾o)(Ｖ＋凾u）＝ｎＲ(Ｔ＋凾s)・・・A
儕儼 の項は無視できるので、 ＰX＋Ｐ凾u＋Ｖ凾o＝ｎＲＴ＋ｎＲ凾s
@ を用いると、 Ｐ凾u＋Ｖ凾o＝ｎＲ凾s ・・・B
これで変化量だけの関係にたどり着けました。
スマートな計算法は、A を @ で辺々で割ることです。 すぐに「1＋微小量」の形が得られます。
（１＋凾o/Ｐ)(１＋凾u/Ｖ) ＝ １＋凾s/Ｔ
１は両辺から消え、２次の微小量を落とせば、 凾o/Ｐ＋凾u/Ｖ ＝ 凾s/Ｔ
一見、B とは異なるように見えますが、同じです。 B を @ で 辺々で割ってみてください。
式として対称性があるだけでなく、圧力が 3％、体積が 2％ 増えれば、絶対温度が 5% 増加する・・・と すぐ分かります。( 0.03 ＋ 0.02 ＝ 0.05)
Q5. 「変化」に対しては 辺々の引き算で対処してきました。
今の場合も A−@ により B が導けます。もちろん、２次の微小量を無視してですが。
これからは、辺々で引くか、辺々で割るか、迷ってしまいそうです。
A. 誰でも迷います。 「辺々で引く」ことが多いので、それを基調にするとよいでしょう。 余裕があれば、「辺々で割る」とよいかも… と思ってみてはどうでしょうか。
Q 全反射についての質問です。 境界面への入射角を θ とし、臨界角を θ0 とします。 全反射する条件は、 θ ＞ θ0 でしょうか、それとも、 θ ≧ θ0 でしょうか。
A. どちらでもいいです。
θ ＞ θ0 なら、まぎれなく全反射しますから、スッキリしているかもしれません。 教科書の多くもそうしています。
入試問題では、出題者が θ ≧ θ0 を誘導していることもあります。 その場合は従ってください。
(※) θ ＝ θ0 のとき 何が起こっているか、興味のある人は『Ｑ＆Ａ 名問の森』を見て下さい。
Q1. 光線が球面に当たったときの屈折はどのように扱えばいいのですか。
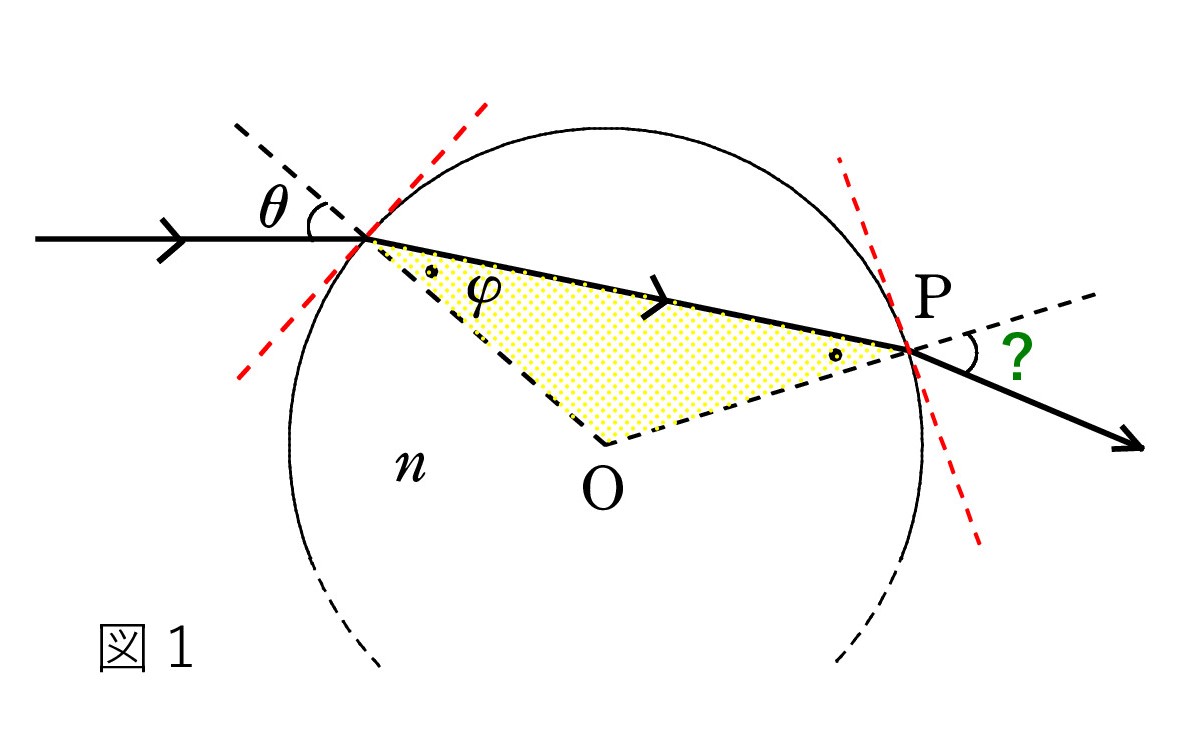A. 図のように、球面に接する平面（赤点線）を考えて対処します。点 O は球の中心です。 入射角を θ 、屈折角を φ とし、球の屈折率を ｎ とすると、ｎ ＝ sinθ / sinφ です。 断りがなければ、空気の屈折率は１と思ってください。
「ｎ sinθ ＝ 一定 」を用いて、
１ × sinθ ＝ ｎ × sinφ としてもいいです。
光が点 P で球を出るときも同様です。 図１では、黄色の三角形が二等辺になっているので、入射角が φ です。
すると・・・ 「？」の屈折角はいくらですか ？
・・・・・・・・？・・・？・・・？・・・？・・・？・・・・・・・・
波は逆行可能 でしたね。 球に入るときの逆行のケース になっています。 そこで、計算しなくても 屈折角は θ になると判断できます。
一般の曲面でも 接平面を考えます。 反射も同じですし、光以外の波でも同様です。
Q2. 平凸レンズ（片面が球面、もう一方が平面）の計算問題で出会ったので質問したのですが、 図１のように球体であれば、虹の原理につながる話ですね。 でも、教科書では 図１とは違う図になっていますが・・・
A. 点 P では反射も起こっています。 屈折と反射は同時に起こります(全反射 は反射だけ)。
虹の場合は、水滴中の P で反射した後 出てくる光が問題です。 図２のようになるので、太陽を背にして虹を見ることになります。
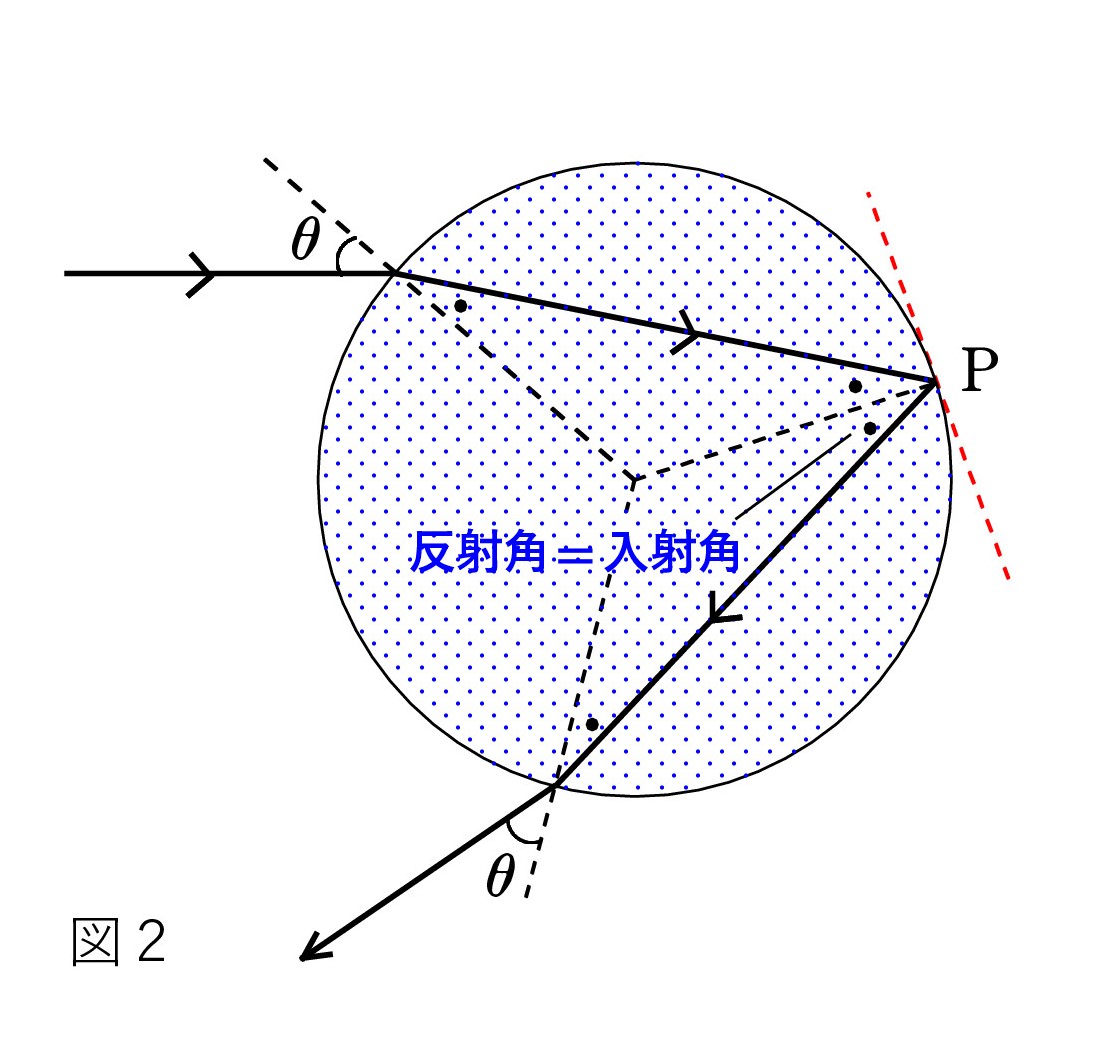
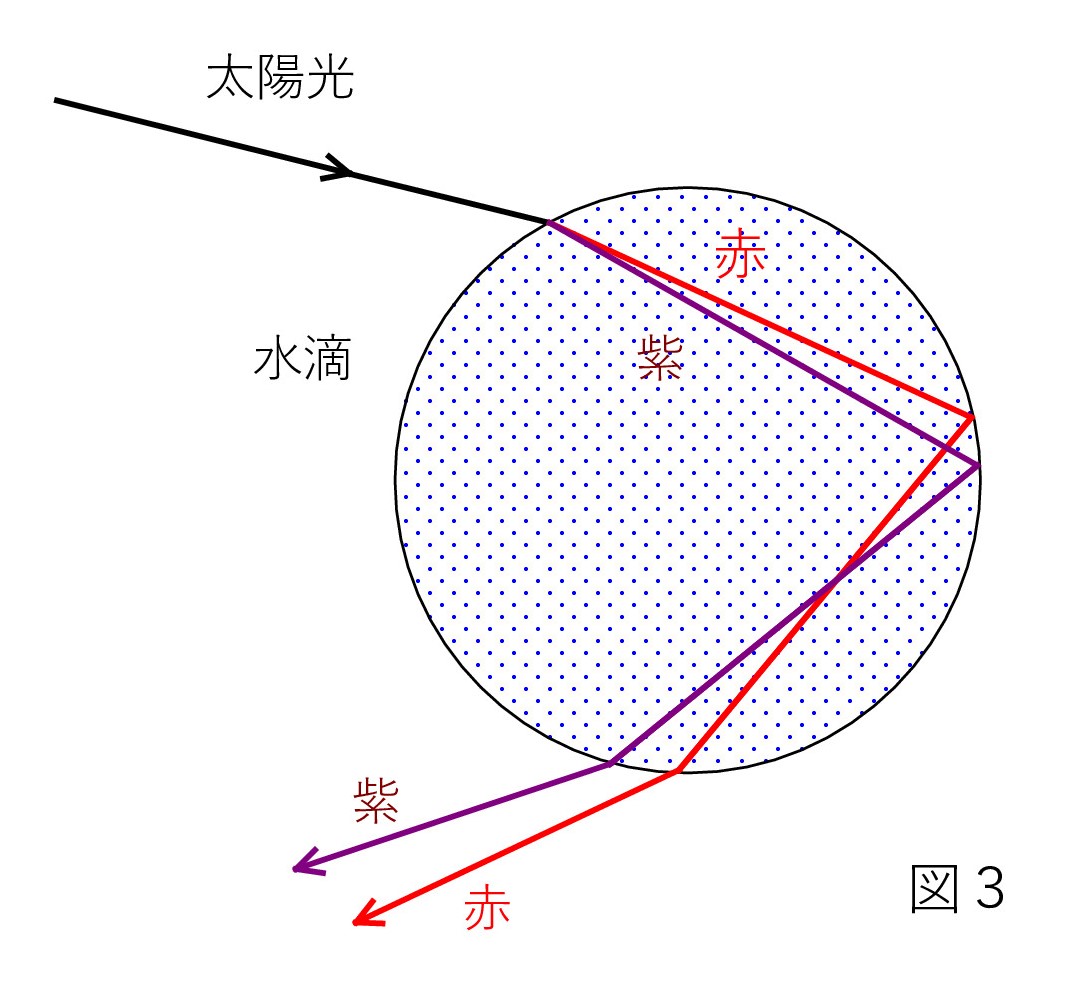
このとき大切なことは、光の波長によって屈折率 ｎ が少しずつ異なるので色が分かれることです（分散）。 波長が短いほど ｎ が大きいので、赤より紫が大きく屈折して、図３のように出てきます。
雨上がりに虹が見られるのは、水滴が漂っていることと、日差しがあるからですね。
rainbow ← rain (雨)＋bow (弓)
では、ここで質問です。 「虹のアーチで、上側は 赤ですか、それとも紫ですか ？」
図３から分かることです。
解答（※※※※）は最後に
Q1. 凸レンズによって物体の実像がスクリーン上にできています。 物体とスクリーンの位置を固定し、レンズを光軸方向に移動させてみると、もう一か所、実像がスクリーンにくっきり映し出される位置があるとのことです。
簡単な見つけ方があると聞きましたが・・・
A. 次図のように、物体が凸レンズの焦点 F の外側にある場合ですね。倒立の実像 ができます。 スクリーンを置けば確認できます。物体を 焦点の内側に置くと、正立の虚像 ができることまでは知っておきたいことです。
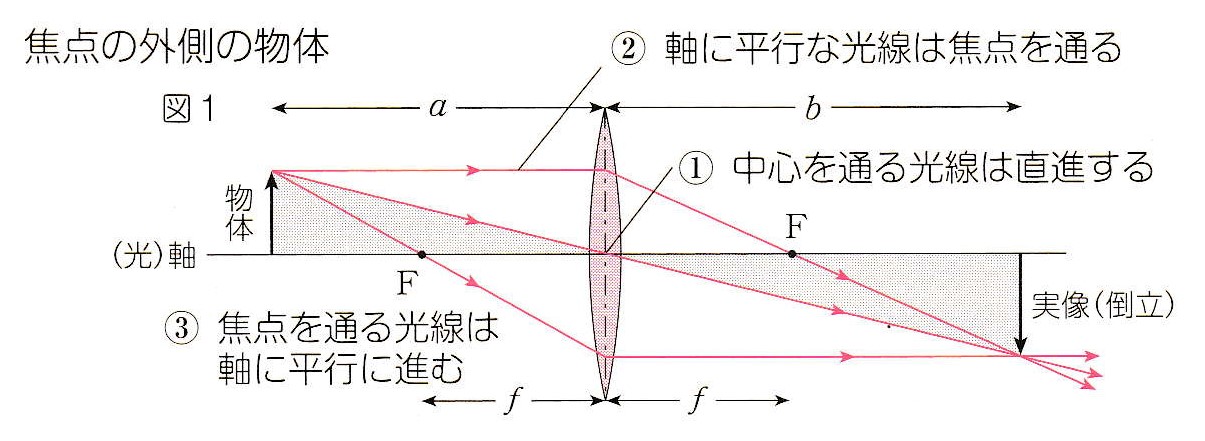
さて、質問のように物体とスクリーンを固定して、レンズを動かす場合です。レンズの公式 1/a ＋ 1/b ＝ 1/f の左辺の項を入れ替えてみると、
1/b ＋ 1/a ＝ 1/f
この式から、物体とレンズの距離を ｂ にすると、レンズから a 離れた位置に実像ができることが読み取れます。 物体とスクリーンの間の距離 a＋b は変えずに済んでいます。
ですから、「物体からレンズをｂ離せばよい」ということです。
Q2. 式で判断するんですね。 作図で示すのは難しいのでしょうか。
A. いや、それも簡単に確認できます。
「波は逆行可能」でした。 そこで、上の図で光線を逆行させてみてください。 実像が物体に、物体が実像に変わりますが、レンズから ｂ 離して物体を置くと、レンズから a 離れた位置に実像をつくる と分かります。
Q3. ついでに確認しておきたいことがあります。 スクリーンを置くのは、実像そのものを見ることができないからですね。
A. 大学の先生でもそう思っている人がいますが、誤解です。
確かに、上の図の状況だと、我々のような立ち位置からは スクリーンがなければ、実像は見えません。
ただ、実像を作った後の、右側に向かう光線に注目してください。 それらが目に入って来るような位置なら実像が見えます。
実際、ルーペ(虫眼鏡) があれば、目から離してみると、向こう側の景色が逆さになって見えます。 それは実像を見ているのです。
上下が逆転しているだけでなく、左右も逆転していることにも注意したいですね。 光軸のまわり、すべての方向について逆転しているのです。 上の図で、矢印を 根元を中心にして、光軸のまわりに一回転させてみれば 納得できるでしょう。 レンズは光軸のまわりで対称的だからだね。
物体が(景色が)180°回転して見えている と言った方が早いですね。
Q4. ルーペは物体を拡大して見たいので、物体に近づけて用います。あれは焦点の内側に物体を置いて、虚像を見ていたんですね。正立の虚像です。いつもそうしてきたので、ルーペを物体からも目からも離して見るのは新鮮な体験でした。確かに倒立の実像が見えました。でも、一部が欠けたりするのはどうしてですか。
A. レンズの大きさと関係しています。
矢印で表した物体の先端から出る光線のうち、レンズの端を通っていく２本を赤で示してみました。これらに挟まれた斜線部でしか、先端は見えないのです。
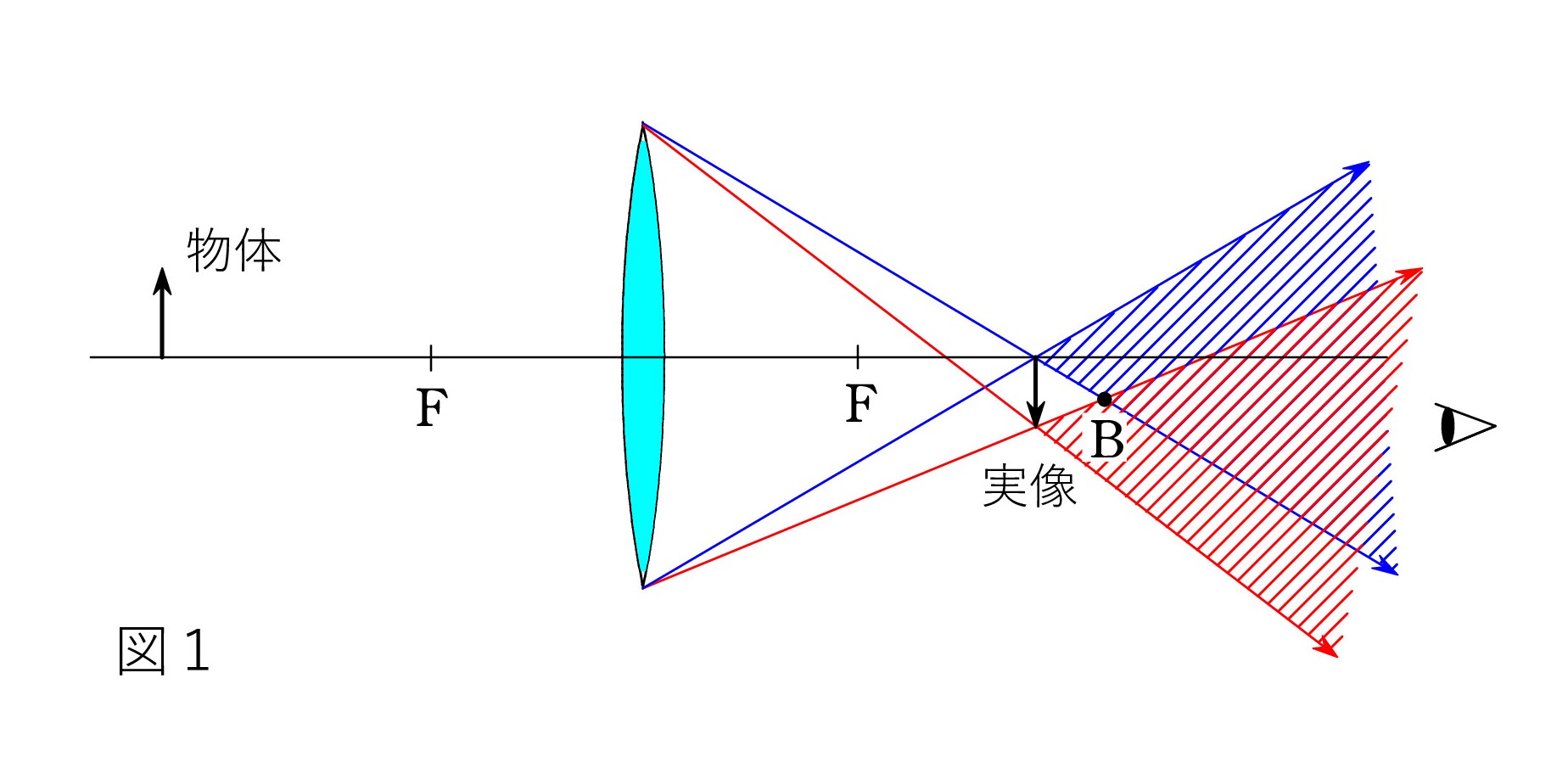
一方、矢印の根本からの光線を青で示しました。矢印全体を見ることができるのは、赤と青の斜線部が重なっている範囲で見るときですね。 それより下では、根本が欠け、上では先端が欠けることになります。
Q5. 赤と青の斜線部のどちらにも入っていない領域からは 実像がまるで見えないということですね。
A. ほぼそうですが、盲点となっている領域があります。 それを説明する前に、話しておきたいことがあります。 ただ、これからの話は入試対策というより、好奇心のある人のためです。
考え方の問題ですが、目の位置を先に決めてもいいのです。
たとえば、実像の先端が見えるかどうかは、目と実像の先端を結ぶ直線を考え、それがレンズに出合うようなら、見えます（図２）。レンズによる屈折光線があるということですから。
この考え方だと、レンズが大きいほど 全体が見えやすいことも分かりやすいでしょう。
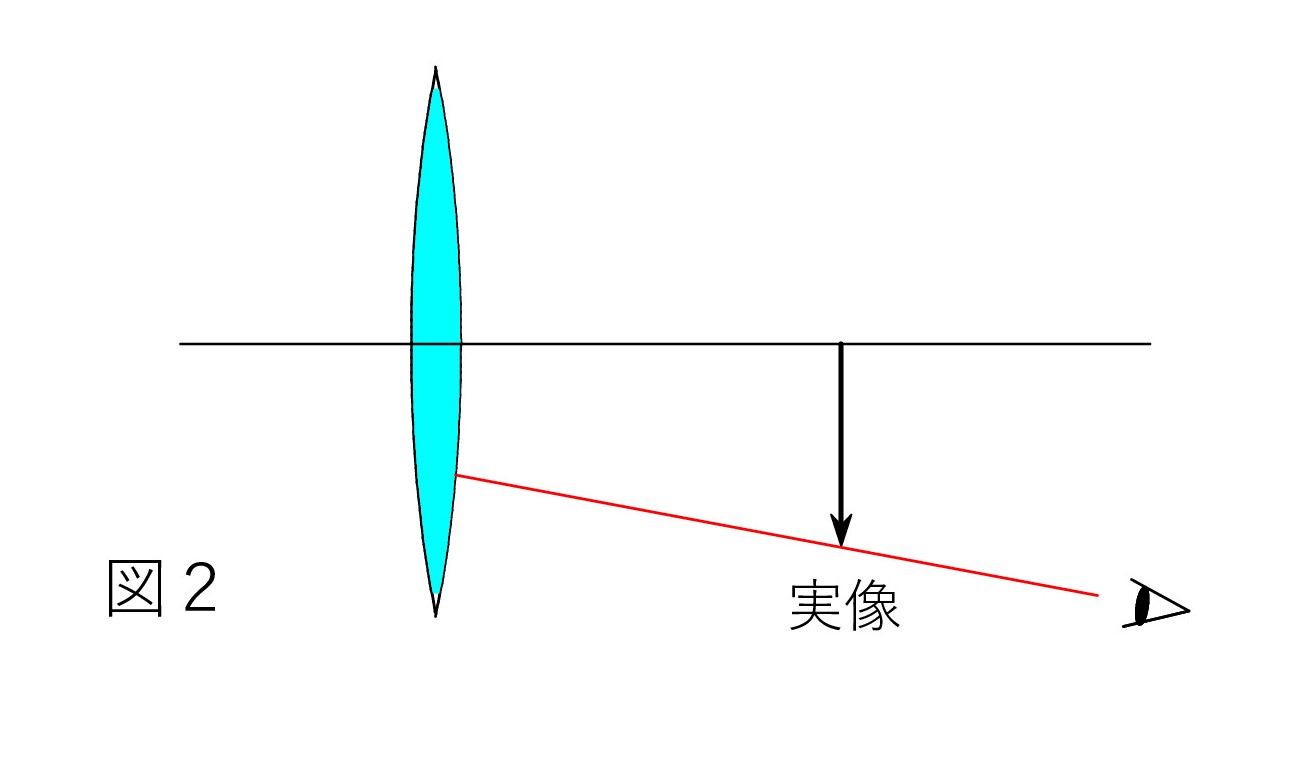
目とレンズの両端を結ぶ直線を引き、その範囲に納まる実像の部分が見えると言ってもいいです。 次図３の位置 A なら矢印の P から Q までが見えます。
全体を見るには位置 B まで離れなくてはなりません。 B は図１でも登場した点です。
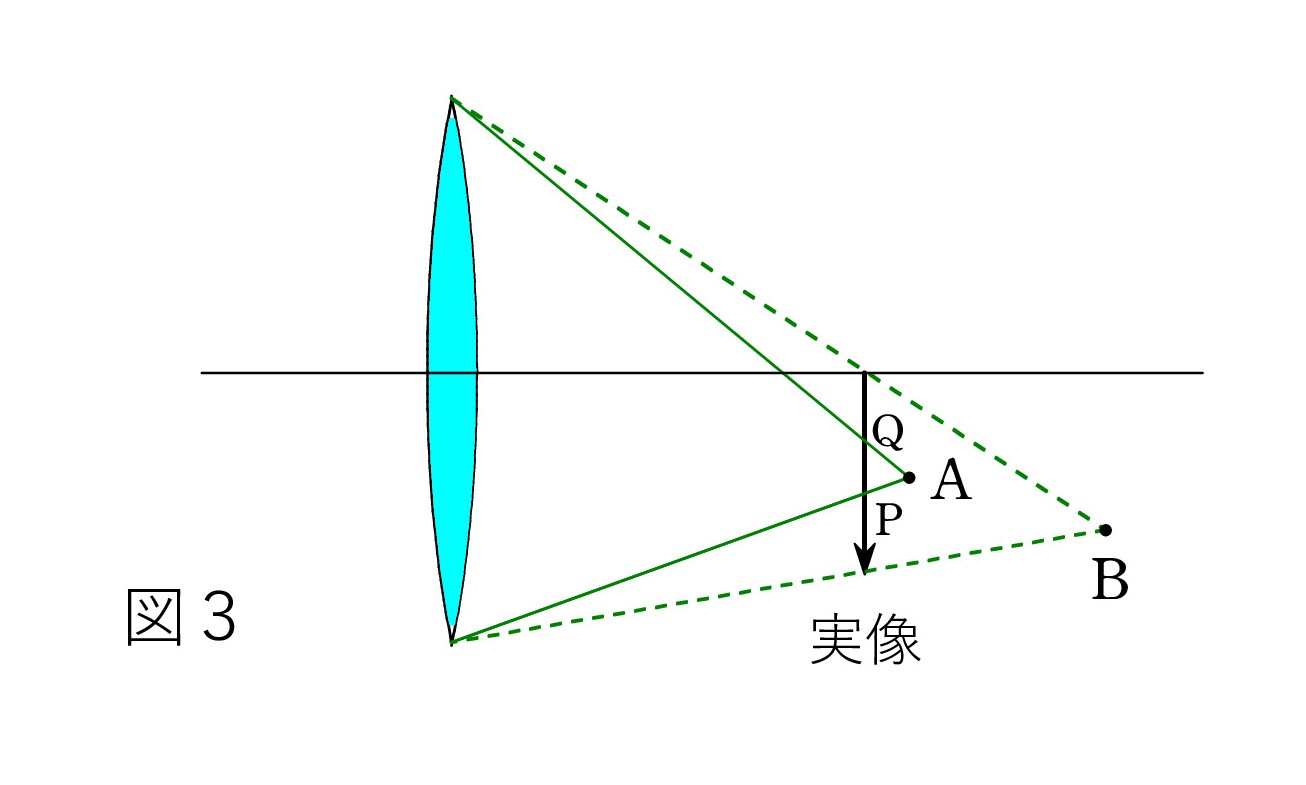
元の話に戻って、実像が一部でも見える領域は、赤・青の斜線部に加えて、実像とB点でつくる三角形の部分を含めないといけないのです。 A 点がある三角形ですね。
では、次の問題にトライ！
「 鏡で全身を見たいとき、必要な鏡の大きさは身長に対してどれぐらいか？」
これは有名な問題で、入試で問われることもあります。
先ほどの話がヒントになるでしょう。 答えを知っている人も理由を考えてください。
解答（※*※）は最後に
電磁気 //////////////////////////////////////////////////////////////////////////////////////////////
Q. ガウスの法則が苦手です。 平面上に電荷が一様に分布しているときの、周りの電場を求めたいのですが・・・。
電荷は正で、面密度を＋σ〔C/ｍ2〕とし、クーロンの法則の定数をｋ〔Nｍ2/C2〕とします。
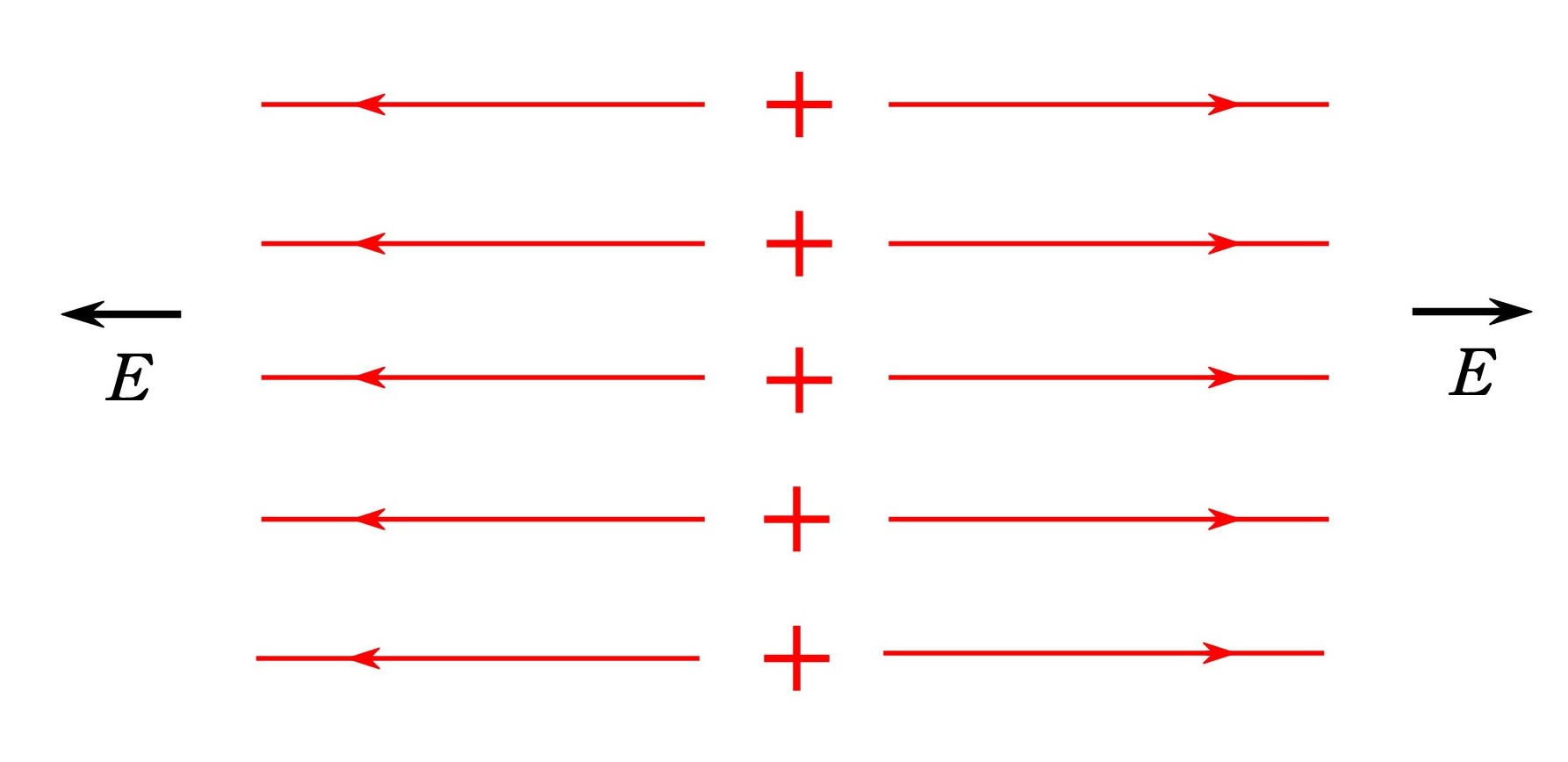A. ＋ からは電気力線が出ます。 対称性から平面に垂直に、両側に均等に出るはずです。 電気力線は平行で等間隔になるので、電場はどこでも一定になります。ある点での電気力線の向き（接線の向き）は電場の向きであり、密集度が電場の強さを表す からですね。
いま、平面上の面積 Ｓ の部分に注目すると、Ｑ ＝ σＳ の正電荷があり、
N ＝ ４πｋＱ 本 の電気力線を出しています――両側に。
そこで、片側では N/２＝２πｋQ ＝ ２πｋσ S 本 であり、 単位面積当たりの本数が電場の強さ E に等しいので、 E ＝ (N/２)/S ＝ ２πｋσ〔N/C〕 と決まります。
〔Nｍ2/C2〕×〔C/ｍ2〕＝〔N/C〕は単位の確認。 （π：パイ、円周率）
誘電率 ε を用いると、N ＝ Q/ε 本 であり、 E ＝ (N/２)/S ＝ σ/２ε と表せます。
４πｋＱ（＝Q/ε）本 は入試では教えてくれることが多いのですが、受験の際は覚えておいた方が安全な公式です。
Q. コンデンサーの問題では、直列や並列の公式を用いなくても、Q ＝ C V と 電気量保存則 で解けると教わりました。
A. 公式に頼らなくても解けるだけの実力を付けよという意味では正しいのですが・・・ 入試では時間を急ぎます。公式はフルに活用しましょう。２個のコンデンサーを１個として扱えれば便利です。
ついでに、知識も利用しましょう。 直列の場合、２つの電圧の比は電気容量の逆比 になります。 電気容量が２C と ３C なら、電圧は３：２です。 全体電圧が V なら、２C の電圧 V1 は V1 ＝ ３V /５ で、電気量 Q は、Q ＝ ２C・V1 ＝ ６C V /５ 直列なので、３C も同じ Q です。 どうです、直列公式を使わずに解けてしまいました！
直列では片方の電圧が尋ねられることが多いのですが、それなら即答です。 入試では知識の多い者が優位に立ちます。
直列・並列で対処できる問題が多いのですが、そうでなければ、いよいよ「必殺技」の出番ですね （エッセンス(下)ｐ58(新版 p63))。
Q. ３つのコンデンサーが直列の場合、たとえば、２C、３C、４C のとき、電圧は逆比だから、４：３：２ でいいですか ？
A. 違います！ 逆比は逆数の比の意味で、１/２：１/３：１/４ になり、12倍すれば、６：４：３ が正しい比です。 全体電圧が V なら、２C のコンデンサーの電圧は 6 V / 13 ですね。
２つの場合は入れ替えですみます。また、直列なら、電気容量が小さいものほど電圧が大きいことも意識しておくとよいでしょう。 たとえば、コンデンサーには耐えられる電圧（耐電圧）がありますが、直列の場合は、容量の小さいものが先に耐電圧に達する可能性から考えます。
以上は、直列では、各コンデンサーの電気量が共通 であることに基づいているので、確認してください。もう一段階戻ると、直列になるには「はじめ電荷なし」か「全電気量 0 」が必要でした。お忘れなく。
Q. コンデンサーの初めの状況が書かれていない問題も見かけますが・・・
A. 初めは電荷なしと考えて解きます。本当は出題者がきちんと宣言すべきことですが、確かにいい加減な出題者はいますね。直列に見えれば、それで O K 。もちろん、電池につながれていれば、初めから電気を蓄えています。でも、電池につなぐ前は電気を帯びていなかったとみなします。
Q. 直流回路の問題で、回路図があり、電圧計や電流計が入っている場合、それらは理想的な計器と思ってよいですか？
A. 断りがなければそう思っていいです。電圧計は内部抵抗が無限大で電流を通さず、電流計は内部抵抗が０で導線と同じということですね。ただ、問題文の全体を見てください。後の方の設問で「内部抵抗はいくらか」とあれば、話が変わります。
ついでながら、電池の内部抵抗も断りがなければ、無視します。
一般論として、状況設定が不明確で二通りの可能性があるときは、解く側は簡単な方を選ぶ権利があります。
Q. 磁場中で、長さｌの導体棒に電流 I が流れていると、電磁力 F ＝ I Bｌ が働きますね （ B ：磁束密度 )。 その作用点は棒の中点と聞きましたが、理由がよく分かりません。
A. 棒を細かく等分割すると、例えば100等分すると、1つ1つに働く力は I B (l/100) ずつですね。これって、重力のときとそっくりだと思いませんか。一様な棒を等分割したとき、どこでも同じ力が働いています。そして、合力 ｍｇ の作用点は重心で、中点でした。類推（アナロジー）で理解できますね。
それでは、一様な棒の重心はなぜ中点になるのでしょう。棒の「対称性から」ならスマートな答えですが、電磁力に対しても通用するように、ていねいに考えてみます。等分割した後、両端の２つの小片に注目すれば、その合力は中点ですね。これで両端２つはなくせます。 次に、新たに両端になった２つに注目し…と、同じことを繰り返していけばいいでしょう。
Q ２本の水平なレール上を質量ｍの導体棒Ｐが滑ります。 Ｐはレールに垂直に置かれ、Ｐとレールの間の動摩擦係数は μ です。
問題集の解答を見ると、動摩擦力が μ ｍｇ となっています。 ２箇所で接触していることを見落としているのではないでしょうか？ μ ｍｇ の２倍になると思いますが・・・。
A. 電磁誘導でよく見る設定ですね。 滑らかなレールがふつうですが、摩擦がある場合も時に出題されています。
動摩擦力Ｆは垂直抗力Ｎで決まります。 Ｆ ＝ μＮ ですね。 レール１本での垂直抗力は 半分（ｍｇ/2）なので、動摩擦力も半分です。 ２本合わせれば、μ ｍｇ です。
なお、棒が一様でない場合、２本のレールからの垂直抗力は異なります。 N1、N2 とすると、力のつり合いから N1 ＋ N2 ＝ ｍｇ であり、重心の位置が分かれば、モーメントのつり合いを利用して、N1 と N2 が求められますが、実は、その必要がないのです。
全動摩擦力は μ N1 ＋ μ N2 ＝ μ ( N1 ＋ N2 ) ＝ μ ｍｇ に他なりません。
力学では自転車や自動車が登場することがありますが、タイヤの本数に関係なく、動摩擦力は μ ｍｇ で扱えます。
静止摩擦力も同様で、レールの本数やタイヤの数には関係しません。
Q1. 電磁誘導の問題 125 (新版 130) では、磁場中で導体棒に外力を加えて一定の角速度 ω で回転させ、問(5)で外力の仕事率をエネルギー保存則から求めています。ダイレクトの計算はできないのですか。
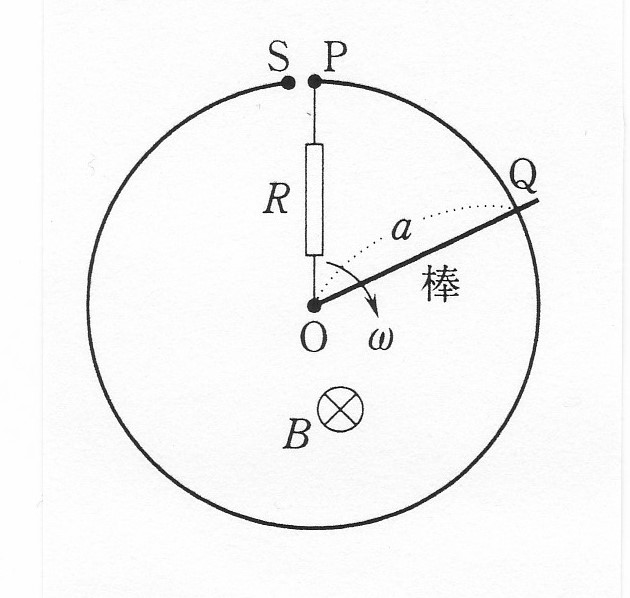
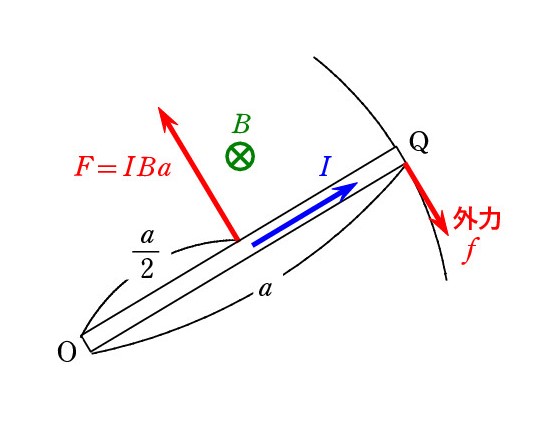
A. できます。 外力ｆを点 Q（正確にはレールとの接点）で加えているとします。
角速度 ω が一定の場合には、力のモーメントのつり合いが成立します。
電磁力 F の作用点は OQ の中点なので、 F × a/2 ＝ ｆ× a ∴ ｆ ＝ F / 2
点 Q での速さをｖとすると、外力の仕事率 P は、 P ＝ ｆｖ です。 円弧に沿って1秒間にｖ〔ｍ〕移動させるからですね。 そして、等速円運動の公式 ｖ ＝ ｒω で r ＝ a なので、 P ＝ ｆ・aω ＝ F a ω / 2
あとは F に問(4)で求めた値を代入してください。
実は、外力を加える位置は棒のどこでもよいのです。 点 О からｒ離れた位置とすると、モーメントのつり合いは、 F × a/２ ＝ ｆｒ ∴ f ＝ F a / 2 r
したがって、 P ＝ｆｖ＝ｆ・ｒω ＝ F a ω / 2
f は ｒ によって変わりますが、仕事率 P に変わりはありません。
エネルギー保存則の観点なら、外力の仕事はジュール熱に等しく、P ＝ R I2 サラッと解決できます。
Q2. 先ほどの問題 125 (新版 130) ですが、回転する導体棒に生じる誘導起電力 V をファラデーの電磁誘導の法則で求めています。問題文の誘導に従えばそうなりますが、公式 V ＝ v B l でも出せるのではないでしょうか。 エッセンス(下)ｐ103(新版 p109) のように。
A. 導体棒に沿って速さが変わっているので、ｖとして平均の速さを用いれば OK です。
点 О での速さは０で、点 Q では aω なので、 v ＝（０＋ aω ）/２
あとは ｌ ＝ a より、 V ＝ v B a ＝ B a2ω /２ ですね。
ちなみに、平均が両端の値だけで考えられるのは、ｖ ＝ ｒ ω のように、ｖ が ｒ の１次式であることに基づいています。無制限ではありません。
Q 高校で教えています。今年(2021年)の共通テストですが、「物理」の電磁誘導の問題では行き過ぎがあると思います。具体的には、第２問・B の問６です。
多くの予備校も「運動量保存に気づけるかがキーポイントで難問」と評価しています。 エネルギー保存を考える生徒はいますが、このような状況での運動量保存には ほぼ全員が出会ったことがないと思います。
A. 初めての共通テストで、どのような問題が出されるのか、大きな関心を集めました。 「物理」全体としては、センター試験と大差ないように思います。 計算力より定性的な思考力が、今まで以上に重視されている ようです。
質問の問６ですが、結論から言いますと、難問ではない と考えています。
まず、状況を確認すると、磁場中で２本の導体棒が滑らかに動き、右側の棒 a だけに初速ｖ0 を右向きに与えます。 動き出した a には誘導起電力 V が生じ、電流 I が時計回りに流れ、２本の棒には電磁力 F が働きます。 棒 a は減速され、棒 b は右に加速されます。 ここまでは 問４と問５で誘導しています。
問６は ２本の棒の速度の時間変化ですが、以上の認識ができれば、４つの選択肢のうち、B か C に限られます。 b にも誘導起電力が生じますが（回路としては a とは逆向き）、a の方が速いので、電流や電磁力の向きに変わりはありません。 a の減速、b の加速が続きます。
やがて、a と b の速さは等しくなります。 すると、両者の誘導起電力は等しくなって電流が止まり、電磁力がなくなります。 結局、慣性の法則による等速度運動に入ります。
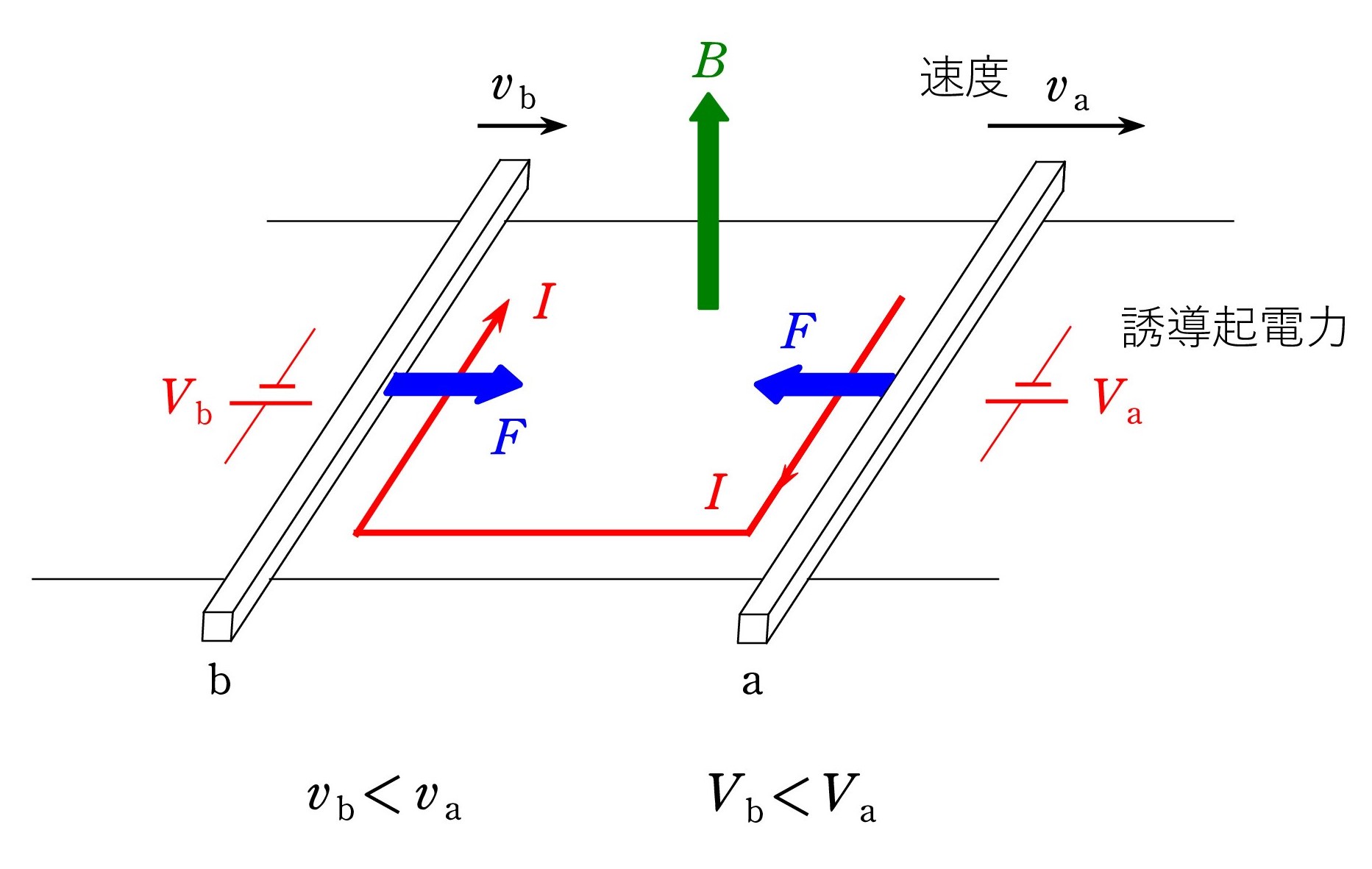
以上、導体棒に生じる誘導起電力 V ＝ ｖＢl で考えてきましたが、ファラデーの法則で考えてもいいでしょう。 途中は上向きの磁束が増し、a と b の速さが等しくなると、磁束は一定になります。
最終速度ｖf を決めるのが運動量保存則です。２つの電磁力の合力は０なので、運動量が保存し、a と b の質量が等しく、ｍ とおくと、 ｍｖ0 ＝ｍｖf＋ｍｖf から ｖf ＝ｖ0 /２ こうして、正解は B になります。
確かに、このようなケースで運動量保存則に気づけというのは、共通テストとしては過酷な要求と思います。 物体系に対して外力が働かない場合、運動量保存則が成り立つ というのが基本ですが、外力が働いても、その和が０であればいい ことまでの認識が求められています。
運動方程式で考えれば、B は選べます。 電磁力の大きさＦが等しく、質量ｍが等しいので、加速度の大きさが等しいのです。 ｖ−ｔグラフの接線の傾き(絶対値)がたえず等しいということです。グラフは対称的になるはずです。
なお、エネルギー保存に目を向ければ、C の ｖf ＝ｖ0 /√２ の場合、全運動エネルギーを求めてみると、初めの a の運動エネルギーと同じであることが分かります。 電流が流れている導体棒には抵抗があるので、ジュール熱が発生しているはずで、C はありえないと判断でき、消去法で B にたどり着けます。
誘導が丁寧で（特に問５）、色々と工夫された設問と思います。 選択肢があるということは、完全に解く必要がないということ でもあります。 基本の学力でも工夫すればできる、思考力を試すとはそういうことではないでしょうか。
珍しい状況設定でしたが、共通テストで出題されたことにより、今後は２次・私大入試でも利用されることは十分考えられます。 まさに運動量保存に気づくことが要求されてくると思います。
Q.
A.
※※※※※※ 解 答 ※※※※※※※※※※※※※※※※※※※※※※※※
※【加速度の最大値 amax の解答】
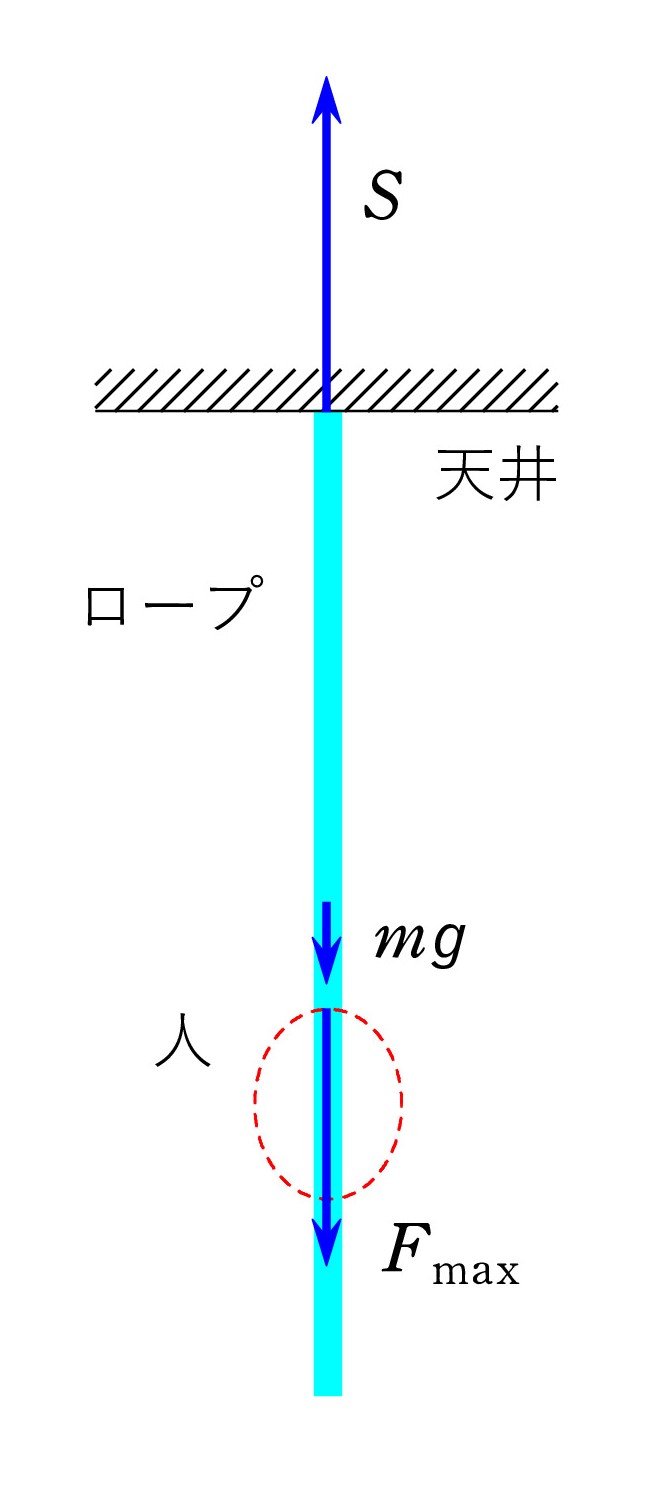amax のときの人とロープが及ぼし合う力の大きさを Ｆmax とすると、人の運動方程式は Ｍ amax ＝ Ｆmax − Ｍｇ
一方、ロープは外れる直前で、全体のつり合い式は、右図から（天井は下向きに S の張力を受け、ロープは上向きに反作用 S を受けている)、
Ｓ ＝ ｍｇ ＋ Ｆmax
Ｆmax を消去し、amax を求めれば、
amax ＝｛Ｓ−(Ｍ＋ｍ)ｇ｝/ Ｍ
「人が静かにぶら下がっただけでは外れない」ことから、
Ｓ ＞ (Ｍ＋ｍ)ｇ であり、 amax ＞０ が保証されている。
人とロープの間の力 Ｆmax と、ロープと天井の間の力 Ｓ・・・それぞれの作用・反作用を分別し、注目物体が受けている力 を取り出すのがキーポイント。
ロープに注目したとき、人の重力 Ｍｇが目に入るようでは ダメ。
問題を進展させ、「ロープ（長さ L ）の下端にぶら下がっている人が天井にたどり着くための最短時間ｔを求めよ」とすれば、amax を調べた意味が分かりやすい。
Ｌ＝1/2・amaxｔ2 として 求めることになる。
人がロープに及ぼす力 Ｆ を一定と考えている人が多い。 確かに、問題としては等加速度運動まで扱いたいので、一定とすることが多い（例外がないぐらい！)。 しかし、運動方程式自体は 力が一定かどうかに関わりなく、成立している。 今の場合なら、Ｆを増しながら登っていき、 Ｆmax を超えた瞬間、ロープが外れるという状況でもよい。
※※【台車上の物体の解答】
(1) Ｐが倒れ始めるまでＰと台車は一体となって運動している。
一体化した運動方程式は、 （ｍ＋Ｍ)α0 ＝Ｆ0 ∴ Ｆ0 ＝（ｍ＋Ｍ)ｇｄ / h
難度が一段階上げられるので、出題者には魅力的で、初めからこのように尋ねられるかもしれません。
(2) 力のつり合いより、 垂直抗力 Ｎ ＝ ｍｇ 静止摩擦力 Ｆ ＝ ｍα0
Ｆ ＜ μＮ なので、 ｍ・（d/h)ｇ ＜ μｍｇ ∴ μ ＞ d/h
等号を含めてもよい。外したのは、倒れ始めるときに滑る心配がないようにという配慮。
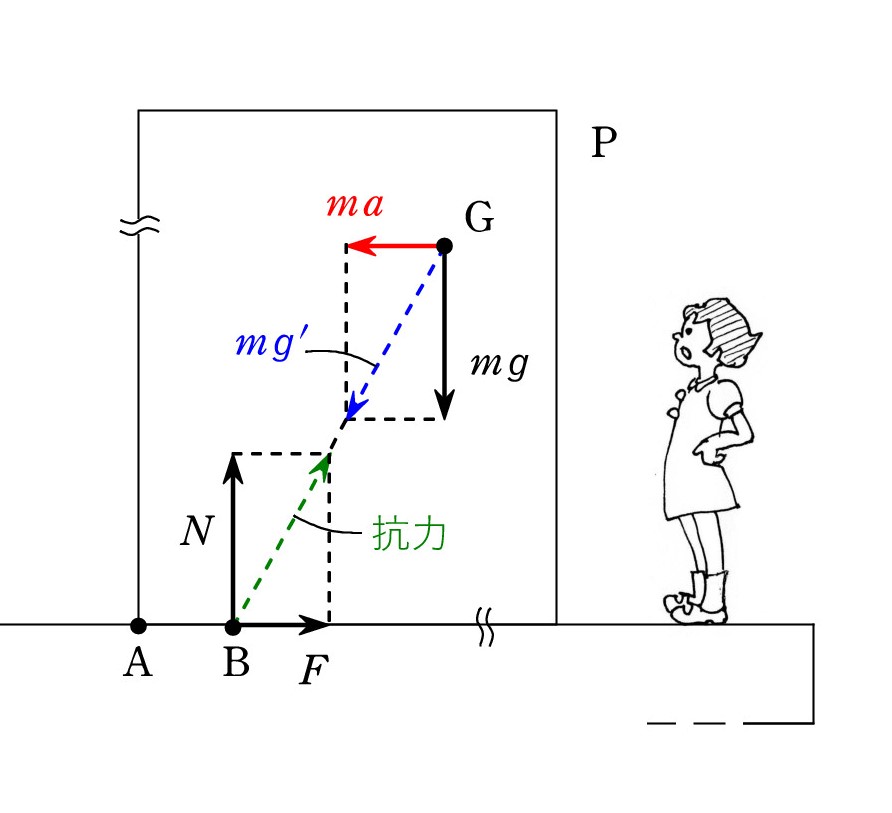(3) 重力と慣性力の合力の作用線がＰの底面と交わる点。見かけの重力の作用線が … としてもよい。
点Ｂになる。 見かけの重力と抗力の２力による剛体のつり合いであり（抗力 ＝ ｍｇ'）、２つの力の作用線は一致している。
見かけの重力の立場では、台車の床は斜面になっている。
α を増していくと、点ＢはＡに近づいていき、α0 でＡと一致する。
※※※【人工衛星と月の図での問いに対する解答】
地球中心からの距離ｒ（円軌道の半径）
ケプラー第３法則により、 T2/r3 ＝ 一定
※※※※【虹の解答】
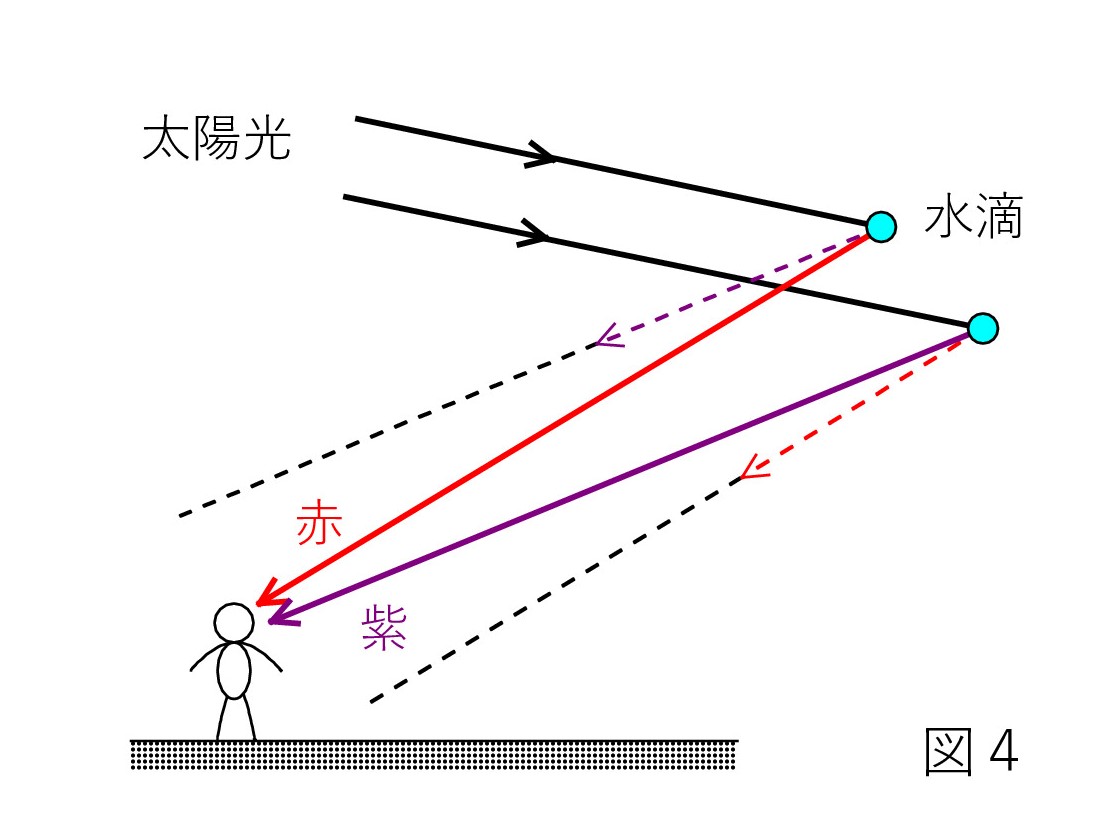赤が上になる。図３では、紫が上になって光が出ているので、誤解が起こりやすい。
図３は１つの水滴での分散を示しているが、人の目に入る光は別の水滴からのものである（図４）。 図３での、地面に対する角度に注目。赤の方が大きい。図３と４は太陽光の方向を合わせてある。
水滴は小さなもので、無数にあり、視線方向のすべての水滴からの光が（赤なら赤が）重なる。 虹の色は 上から、赤・黄・青・紫 の順になる。
飛行機から太陽を背にして虹を見下ろすと、完全なリングになって見えることがある。もちろん、外側が赤。
洗車や庭用の散水ホースがあれば、シャワーにして、太陽を背に水滴をばらまくと、虹がクッキリ見える。 その少し外側にはもう一本の虹が淡く見える。副虹と呼ばれているが、水滴内で２度反射してから出てきた光である。空にかかる虹でも、見られることがある。
「虹はどこにあるの？」という疑問には、「物ではないから、どこにもない。そう見えているだけ」と答えることになるが、禅問答に近く、相手は納得してくれないであろう。光が生じた場所なら答えることができ、「水滴がたくさん漂っている所」となる。遠いか近いかは何とも言えないし、隣の人にとっての水滴は自分と同じものではない。
※*※【鏡の解答】
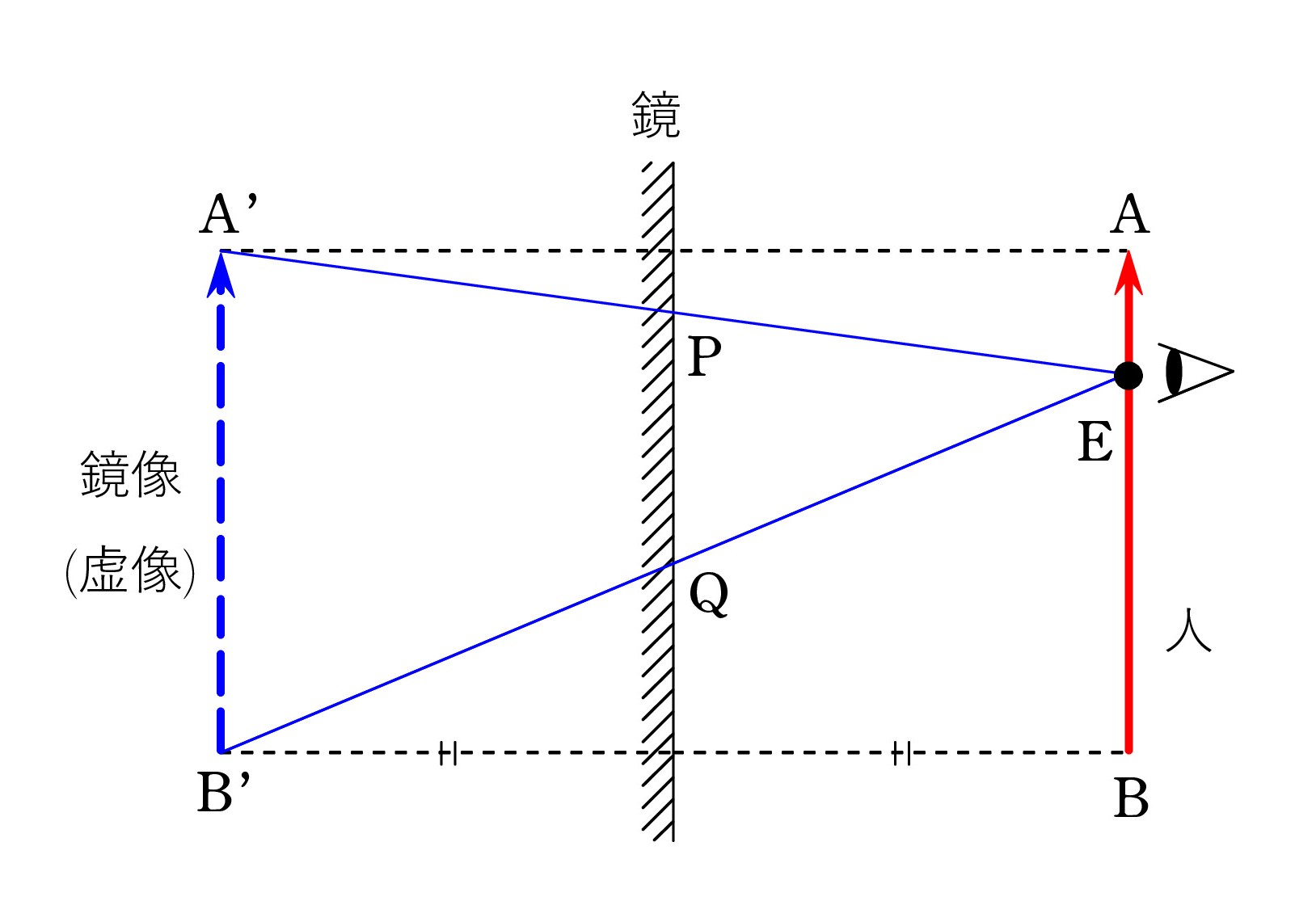人を矢印 AB で表す。鏡像 A’B’ は鏡に対して対称な位置にできる。 目 E と A’、B’ を結ぶ直線を描けば、鏡との交点 P、Q が確認できる。P での反射により頭の先 A が見え、Q での反射により足もと B が見えるので、PQ 間の鏡が必要な部分である。
△EPQ と △EA’B’ は相似で、相似比は１：２だから、PQ ＝ A’B’/2 ＝ AB /2、つまり、鏡は 身長の半分でよい。
目の位置(高さ) E には関係しないことも確かめておきたい。
また、人が鏡から離れても、近づいても、全身を見ているときに役立っている鏡 PQ は身長の半分である。
しかも、PQ の位置そのものが変わらない。つまり、PQ 間以外の鏡をなくしても、人は鏡からの距離に関わらず、全身を見られるのである（解答を書いていて気が付いたこと！)。
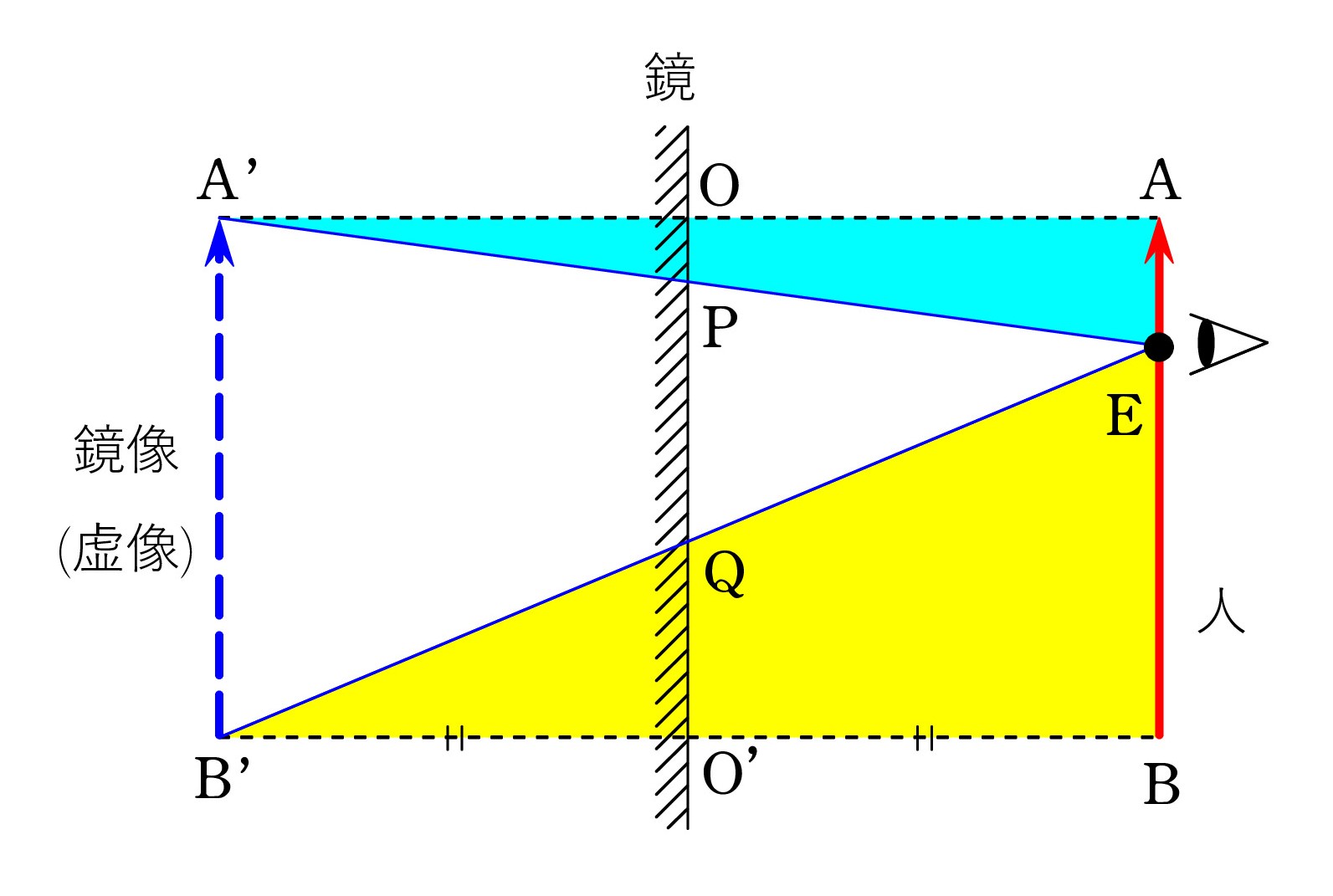(証明) 直線 A’A と鏡の交点を O とする。 空色の直角三角形 △A’OP と △A’AE は相似で、相似比は １：２。 よって、OP ＝ AE/2 。 鏡からの距離 OA が変化しても AE は一定だから、OP も一定。そして、 O は定点だから P も定点。
同様に、直線 B’B と鏡の交点を O’ とすれば、黄色の △B’O’Q と △B’BE が相似で、 EB が一定であることから、Q は定点であることが示せ、線分 PQ は不変となる。
PQ ＝ 一定(身長の半分) なので、P (または Q ) が定点であることを確認するだけでもよい。
【質問について】 メールでの質問は次のアドレスまで。 hiroba@mb.ccnw.ne.jp
手紙またはFAXでの質問は河合出版を通してください。電話は、正確に伝わらないことが
ありますので、できるだけ避けてください。
トップページに戻る