Dialogue 　　　　　対話形式の Q＆A です。　□ をクリックすると記事に飛べます。


□　物体系　・　垂直抗力の仕事　・　保存則

□　衝突　・　保存則　・　重心系

□　遠心力と慣性力　・　単振り子　・　万有引力

□　単振動　・　Ｆ＝−Ｋｘ　・　エネルギー保存則

□　コンデンサー　・　多重極板　・　ガウスの法則









入試一般　　//////////////////////////////////////////////////////////////////////////////////////////////




Q.　試験で、解けそうもない難問に出会ったとき、どうすればいいでしょう？


A.　難問が解けなくても合否には影響しない という事実を思い出して、落ち着くことが第一です。
　そして、似た問題に出会ったことがないか思い出してください。なんとなく似ているでいいのです。電磁気の問題で力学の問題につながることもあります。実は、大学もそんな発想で作問していることはよくあります。物理の思考法としても大切なものです。

　解けない設問に至るまでの設問を見直す ことも大事です。誘導になっていることが多いからです。特に前問ですね。 さらには、その後に登場してくる問題文を読んでみるとヒントになることもあります。

　連立方程式が閉じない場合、条件の見落としが考えられます。物理的な 対称性 が利用できるかもしれません。
　どうしようもなくなった時は、「困ったときは、エネルギー保存！」と呪文を唱えてみましょう。　実際、私自身それで救われたことがあります。　まあ、もう少し一般化すれば、「保存則に注意！」ですね。

　「自分だけが知らないのかも…」と思ったら、もう負けたも同然です。「初めての問題だから、周りも同じはずだ」と思えるだけの問題量を身につけておくのが何よりですね。エッセンス・風・森 と仕上げておけば大丈夫。




Q.　志望大学の問題を見たら、大変な長文の問題です。「森」で大丈夫ですか？


A.　長文問題は、実際には２つ、ないし３つのテーマがつなげられています。　一つ一つに分ければ、「森」の内容と変わりありません。　つまり、長文対策というものは必要ありません、というか、対策などないのです。




Q.　現役生で、共通テストが終わった段階です。「風」はもちろん、頑張って「森」の重要問題までは仕上げました。　でも、「森」の残り全部をやる余裕はないと思います。　今後どうすればいいでしょう。　　　　＜入試直前＞


A.　「風」レベルの標準的な入試問題をやりましょう。＜腕組み勉強法＞と呼んでいますが、問題文を読み、解決に至る筋道を思い浮かべます。計算はしません。そして、すぐ解答を見ます。思った通りの解き方であれば、それで OK 。
　たとえば、衝突の問題なら・・・運動量保存と反発係数の式の連立で解けるはずと見通しを立てた段階で、次の設問に進みます。　筋道が描けない場合は、普通に鉛筆で解きます。　それも図を描いたりして、解決策が立てられれば、それでおしまい。

　この方法の良さは短時間に多くの問題に出会えること。　今までの復習になり、未経験の問題にも出会えます。　　入試という限られた解答時間内には、やったことのある問題か、それに近い問題までしか解けない のです。 だから、いろいろな顔つきの問題に出会っておきたいのです。　現役生共通の弱点 が 問題量の少なさ です。

　注意点が二つ。　難問題は避けること。腕組みで解けることはないでしょうし、何より 入試で出会う可能性が低いのが難問 です。　もう一点は、この方法はあくまで入試直前という緊急対策用です。　即効性があり、非常に効果的ですが、本来の勉強法ではありません。

　思考力を鍛える効果も大きい のです。　将棋で言えば、駒を動かさずに考えるのと同じです。　問題文がこの先何を尋ねてくるかまで予想しながら 取り組みましょう。
　普段の勉強でも時々やってみる価値があります。　問題に掲げられている図を見ただけで、全容が予想できるようになったらプロ並みです。

　「森」の残りの問題ですが、「重要」の指定がないということは一般に難問です。　問題文を読み、設問ごとに少し考えてから、解説を読んでしまうという非常手段があります。　聞きかじっただけの＜耳学問＞に近いですが、類型に出会っておけば、実際に出題されたとき、まるで違います。　解説を読んで理解すること自体が勉強になります。
　「森」に掲載されている以上、「難問を出す難関大学」対策としては出会っておきたい問題なのです。

　＜腕組み勉強法＞を主にし、たまに＜耳学問＞を織り交ぜていくとメリハリがつきます。　腕試しとして赤本をやるのもメリハリ付けと思ってください。５年分もやれば十分でしょう。

　











力 学　　//////////////////////////////////////////////////////////////////////////////////////////////






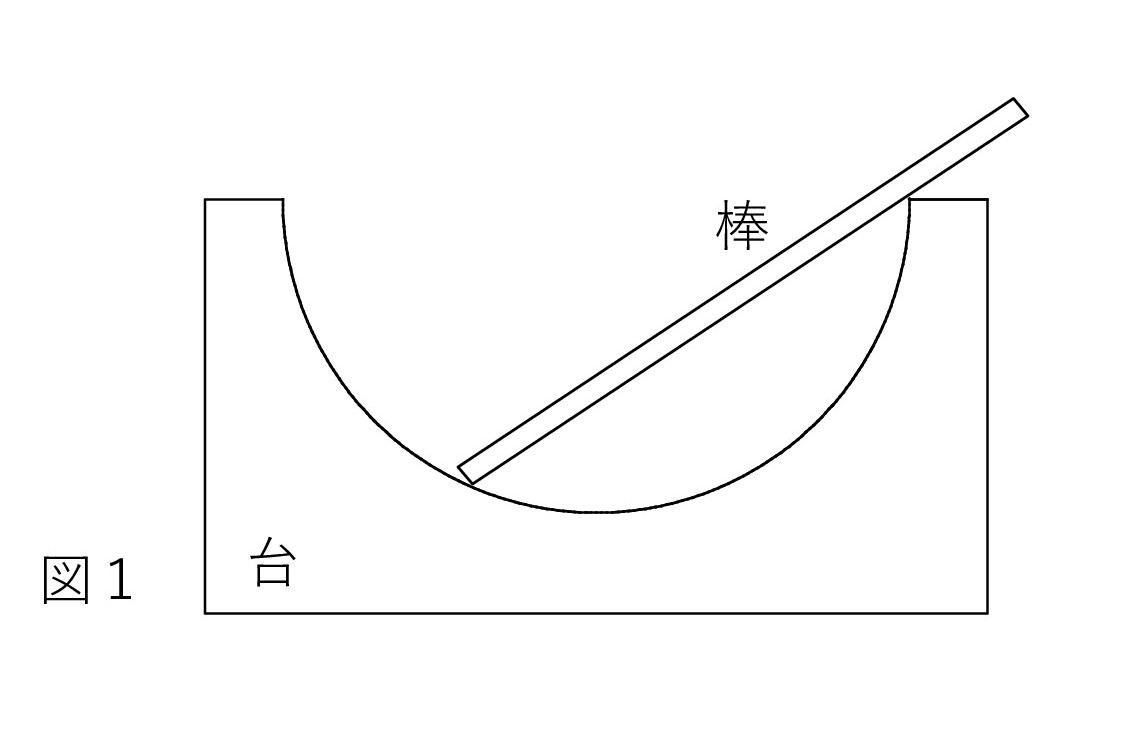
Q.　球面（半球面）をもつ台上に置かれて静止している棒が、台から受ける垂直抗力を矢印で図示したいのですが、向きがよく分かりません。



A.　Ａ 点では、球面を平面に置き換えて考えます。　曲面も狭い範囲で考えれば 平面と同じです。　つまり、接する平面（赤点線）を考え、それに垂直に垂直抗力 Ｎ_A を描きます。　球面なので、Ｎ_A は球の中心 O を指します。

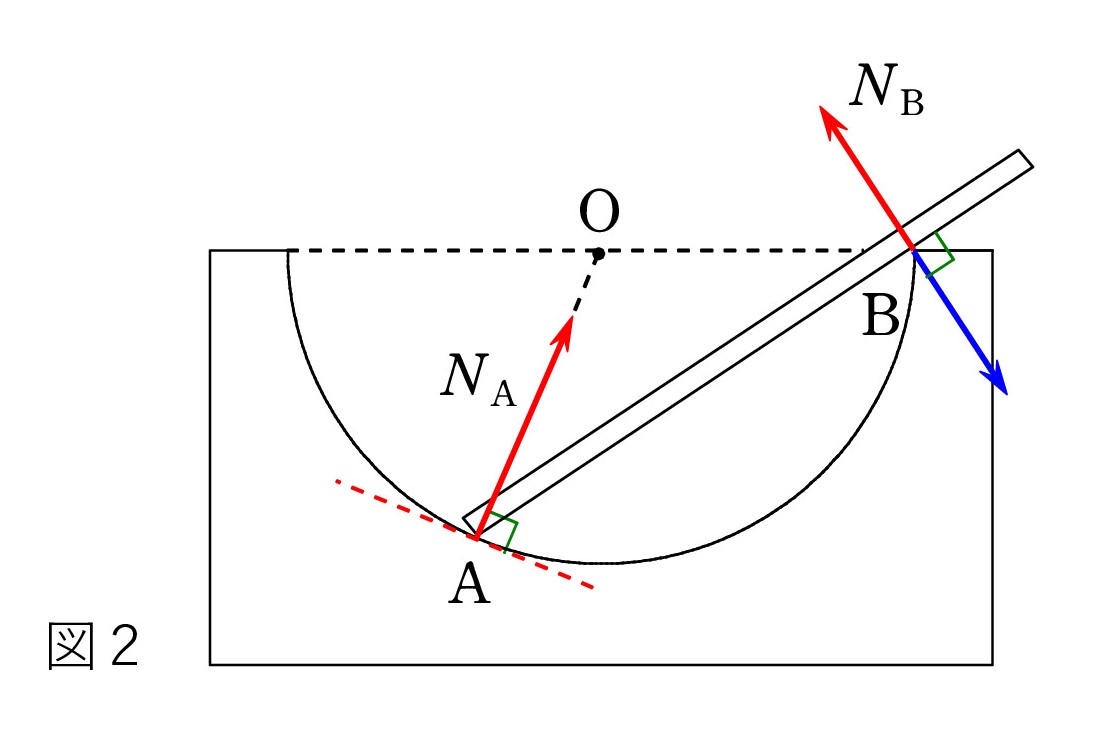　Ｂ 点の場合には、台の角に接する平面が分かりません。　そこで、逆に、台の角が棒から受ける垂直抗力を考えます。　棒に垂直なので、青矢印のようになります。　次に、作用・反作用の法則 により、その反対向きと判断して、赤の Ｎ_B を描けばよいのです。
　描けた人も「何となく」だったり「不安感を抱えながら」だったのではないでしょうか。　理屈が分かれば自信を持って対処できます。

　要するに、　台か棒か、どちらかの平面（あるいは 接平面）が目に入れば、それに垂直な方向です。　B 点の場合もいきなり赤矢印が描けるでしょう。

　摩擦がある場合には、平面（あるいは 接平面）方向に摩擦力を用意します。　ただ、摩擦の向きが２通りのどちらになるかは、状況に従って考えます。

　では、問題です。

　　　図２で、摩擦がないとします。そして、棒は一様ではなく、細いとします。
　　　　　　　　　　 　　棒の重心はどこにありますか ？

　　　　ヒント：　作図で決めます。　重力を含め３つの力が働いています。

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　解答(※�T※)は最後に掲載しておきます。






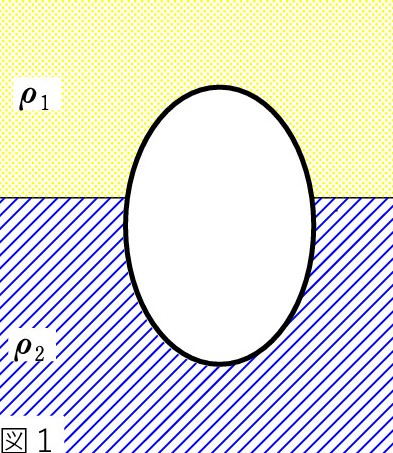
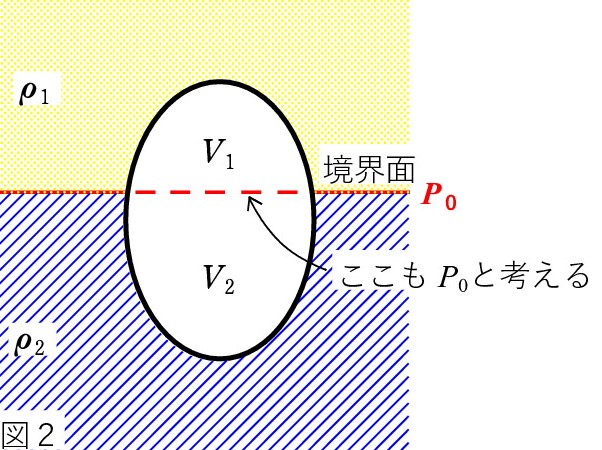
Q1.　浮力の公式 ρ V ｇ は知っていますし、理解もしている積もりです。 ρ は液体の密度で、V は液面下の体積です。しかし、図１のように、物体が２つの液体にまたがって浸かっているときの浮力 F はどうなるのでしょうか？　液体の密度を ρ₁、ρ₂ とします。



A.　図２のように、液体の境界面の延長（破線）で物体を分割し、上下の体積を調べます。　V₁、V₂ とすると、
　F ＝ ρ₁ V₁ g ＋ ρ₂ V₂ ｇ です。
　そう思った人は多いと思いますが、なぜか説明できますか ？
　自分なりの考えをまとめてから、以下を読んでください。




　　　　　・・・・・・・・？・・・？・・・？・・・？・・・？・・・・・・・・




　V₁ の部分を ρ₁ の液体に置き換え、 V₂ の部分を ρ₂ の 液体に置き換えてみるのがスマート でしょう。置き換えれば、２つの液体が重なっているだけのことで、全体のつり合いは保たれます。置き換えた液体は浮力 F で支えられているのです。よって、浮力 F ＝（置き換えた液体の重力）であり、右辺は上式で表されます。「エッセンス」(上) p26 の アルキメデスの原理 の応用ですね。
　物体の形状が任意であることも理解できます。

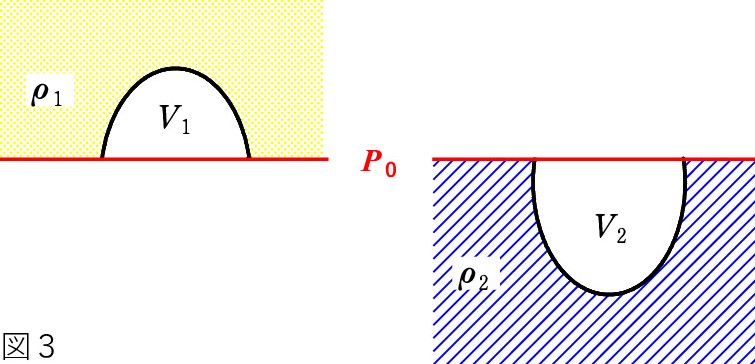
　あるいは、図２のように、２つの液体の境界面での圧力を P₀ とし、物体内の破線部も P₀ として考えます。すると、図３のように、まさに２つの物体がそれぞれに受ける浮力の問題と同じになります。
　破線部で物体に働く P₀ による力は、断面積を S として、上向きに P₀ S 、下向きに P₀ S で、力のつり合いを壊しません。　現実には、物体内の破線部の圧力は P₀ ではなく、形状によっては一定でさえないのですが、「 P₀ とみなしてしまう」のが Key ですね。
　破線部に液体を浸み込ませ、圧力 P₀ の薄い層を作ったとして考えてもいいでしょう。

　　　　　

Q2.　なるほど！ ですね。 アルキメデスの原理の理解が深まりました。　 ただ、直方体（あるいは円柱など）の場合なら、 「 浮力は圧力差で生じる」との観点で、浮力 F を計算で導くことも可能では ？


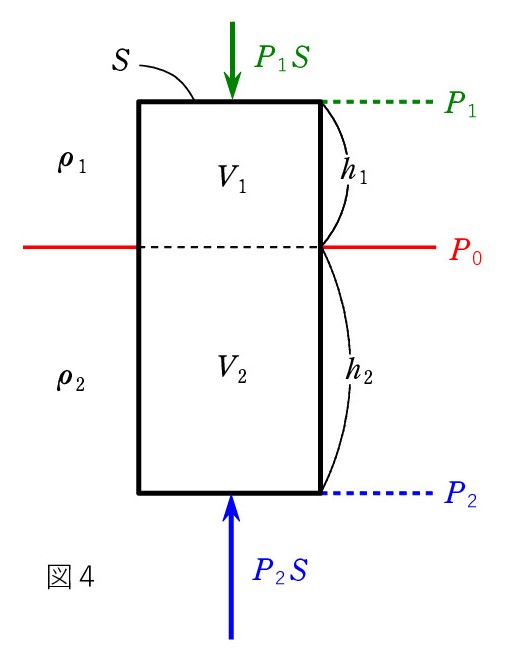A.　圧力の公式　ρｇｈ を用いてできます。
　図４のように、上面での圧力をＰ₁ とすると、
　　　　Ｐ₀ ＝ Ｐ₁ ＋ ρ₁ｇｈ₁
次に、底面での圧力 Ｐ₂ は、
　　　　Ｐ₂ ＝ Ｐ₀ ＋ ρ₂ｇｈ₂ ＝ Ｐ₁ ＋ ρ₁ｇｈ₁ ＋ ρ₂ｇｈ₂　
そして、断面積を Ｓ とすると、
　　 　F ＝ Ｐ₂Ｓ − Ｐ₁Ｓ ＝（Ｐ₂ ― Ｐ₁) Ｓ
　　　　 ＝ （ ρ₁ｇｈ₁ ＋ ρ₂ｇｈ₂ ）Ｓ ＝ ρ₁Ｖ₁ｇ ＋ ρ₂Ｖ₂ｇ


　ρ₁ ＝ ρ₂ の場合、浮力の公式 ρ V ｇ に戻ることをチェックしておきたいですね。
複雑化された条件での答えを得た場合、単純なケースでの答えを含むはず です。

　図１の場合は、鉛直方向に細長い直方体の集合（真上から見れば、網目模様）と考えれば、済みます。　網目を細かくしても、上面と下面には傾きがあって、直方体にはならないという心配をする人もいるでしょう。『Q＆A 風』で話したピストンに加わる大気の力と同じで、大丈夫です。


　ついでながら、いまの場合は　ρ₁ ≦ ρ₂ です。　ρ₁ ＞ ρ₂ は 液体が不安定になります。下の液滴が上に入ったとき、浮力が優って上に上がり続け、上の液滴が下に入ったときは下がり続けるからです。
揺れなどちょっとしたきっかけでバランスが崩れ、上下が入れ替わります。　密度が大きい水の上に軽い油がある状態は安定ですが、逆は不安定です。







Q.　慣性力は見かけの力といわれるように、用いなくても、静止系で解けるはずです。　計算が楽になるかもしれませんが、そんな程度のことなら、認めない方が物理の姿勢としては好ましいと思うのですが・・・


A.　計算しなくても、何が起こるか 分かるのが 慣性力の魅力 です。　　たとえば、
　加速している電車の中で、ボールを斜めに放り投げたとします。車内で見ると、どんな軌跡を描くでしょうか ？
　電車の加速度は一定とし、空気抵抗は無視です。

　答えは放物線です。「なーんだ」と思いますか。ただの放物線ではないのです。　先を読む前に少し考えてみてください。　なぜ、放物線といえるかも含めて。




　　　　　・・・・・・・・？・・・？・・・？・・・？・・・？・・・・・・・・




　ボールが飛んでいる間も慣性力は水平方向で働き続けます。一定のベクトルですね。　　重力との合力も一定のベクトルになり、「見かけの重力」と認識すれば、もういいですね。　普通の世界の知識が活かせて、軌跡は放物線。　ただし、その軸は 見かけの重力方向 です。
　念のためですが、車外の人が見れば、鉛直方向を軸とする放物線で、先ほどの放物線とは形状が異なります。見えている初速度も加速度も異なるためです。

　では、もう一つ質問。
　電車の中には水槽が置かれています。水中でプラスチックの軽いボールを放すと、どのように浮いて来ますか ？




　　　　　・・・・・・・・？・・・？・・・？・・・？・・・？・・・・・・・・




　まず、「エッセンス」の復習ですが、水面はどうなっているかというと……　「水平」ですね。（上）ｐ70 (新版 p 72)　もちろん、見かけの水平方向で、見かけの重力に垂直な方向です。　さて、普通の世界では浮力は重力の逆向きに働きます。これは圧力（水圧）が重力方向で増していくからです。　浮力は圧力差で生じる のでした。
　この知識を活かせば……　ボールは見かけの重力の正反対の向きに上がってくる と断言できるのです。

　車内で風船を放せば ？ ……　その動きも同じですね。　車内の空気にも圧力差が生じているのです。　大気圧は一定というのは大まかな話です。上空へ向かえばわずかずつ下がっていきます。 水圧も大気圧も原理は同じこと です（この認識をもっていた人はすばらしい！）。

　どうですか。計算なしでこんなにも多くのことが予測できたのです。
　まさに 慣性力の威力！! ではないでしょうか。
　
　以上のことは図を描くと分かりやすいのですが、あえて図なしで考えてみてください。
　そして、　自分なりの説明図を描いてみてください。
　　　　　　　　　　　　　　　　　　　　　　　　　　図解(※�U※)は最後に掲載しておきます。

　










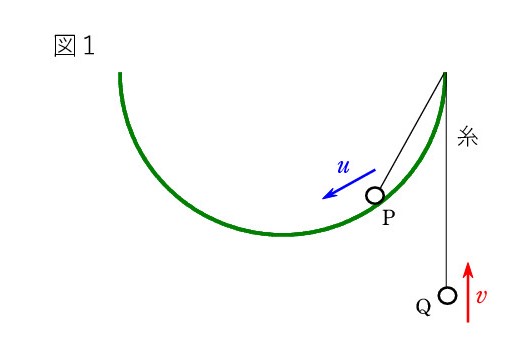
Q1.　図１のように、糸で結ばれた２つの小球 P、Q があり、P は半球面上を速さ u で滑り降り、　Q は上に速さ ｖ で上がっています。 当然、 u ＝ v　だと思うのですが・・・、答えが合いません。
　なお、半球面は固定されています。


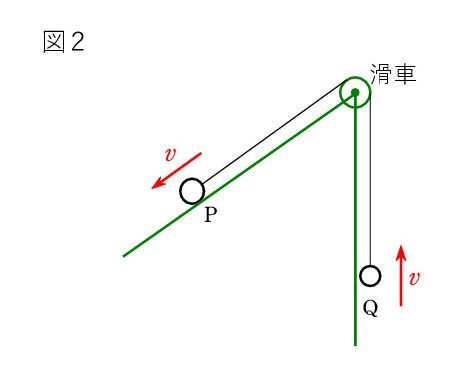
A.　今まであなたが出会ったのは、２つが糸の方向に動く場合ばかりだったのではありませんか？　たとえば、図２のような斜面の場合には、２つの速さは同じです。これは「糸の長さが一定」だからです。P が斜面に沿って１ｃｍ 降りれば、Q は１ｃｍ 上がります。同じ時間内のことですから、２つは同じ速さです。　つまり、糸方向の速度成分は一致する のです。
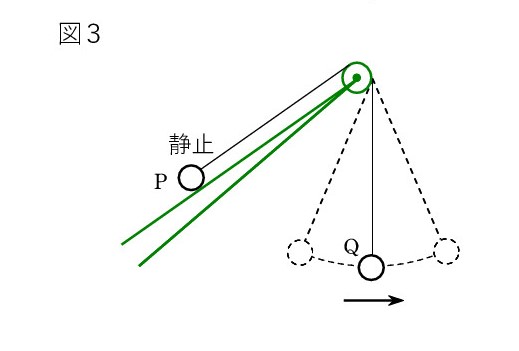
　ところが、糸に垂直な速度成分は無関係です。 分かりやすい例が 図３で、P を止めておいて、Q を振らせば、Q の速さはいくらでも構わないのは明らかでしょう。糸方向の成分は０と０で、一致しています。

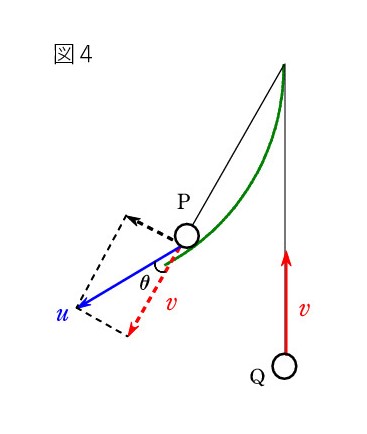
　さて、図１のケースですが、図４のように P の速度は円の接線方向で、糸方向の成分が Q と同じ v なので、
　u cos θ ＝ ｖ が正しい関係ですね。 θ は問題文で分かるようになっているはずです。

　難問に出会うことによって、それまで何気なく通り過ぎていたことの真の意味に気づく ということがよく起こります。「分かった！」と叫びたくなる一瞬ですね。

　　　　

　状況からすると、摩擦がなく、力学的エネルギー保存則で解く問題でしょう。 静止状態から始まっていれば、P と Q の物体系に対して、
　 （Pが失った位置エネルギー）＝（Pの運動エネルギー）＋（Qの運動エネルギー）
　　　　　　　　　　　　　　　　+（Qの位置エネルギーの増加）

　このように （失ったエネルギー）＝（現れたエネルギー）の見方 なら、位置エネルギーの基準は気になりません。




Q2.　先ほどの件は解決できました。もう一つの質問です。上の図１で、初め P は半球面の縁から動き出します。その直後の加速度が問われています。どうしたらいいか、見当がつきません。半球面にも縁にも摩擦はありません。


A.　「直後」がポイントですね。P は縁にいるので、半球面は鉛直な壁と同じです。もっと分かりやすく言えば、糸が摩擦のない滑車にかけられて、P と Q が鉛直に運動するケースに該当しているのです。加速度を a 、糸の張力を T とおいて、P と Q の運動方程式を連立で解く、いつもの問題ですね。『Q＆A 風』で話した「１次元化 ＋ 一体化」なら、
　　　　a ＝（ ｍ−M )ｇ /（ ｍ＋M ）と 即答です。　　（ 質量　P : ｍ 、 Q : M ）

　一般に、「直後」の問題は何かが単純化されています。ある量が特殊な値になっていることもあります。たとえば、電気回路でスイッチを O N した直後、コイルの電流が０だったり、（帯電していない）コンデンサーの電圧が０だったりです。　「直後問題は計算が楽なはず」と思って取り組むと、「何か」が見つかりやすいと思います。









＃＃＃　Dialogue （対話）：　Q1 〜 Q15　＃＃＃＃＃

　　――――――　物体系　・　垂直抗力の仕事　・　保存則　――――――



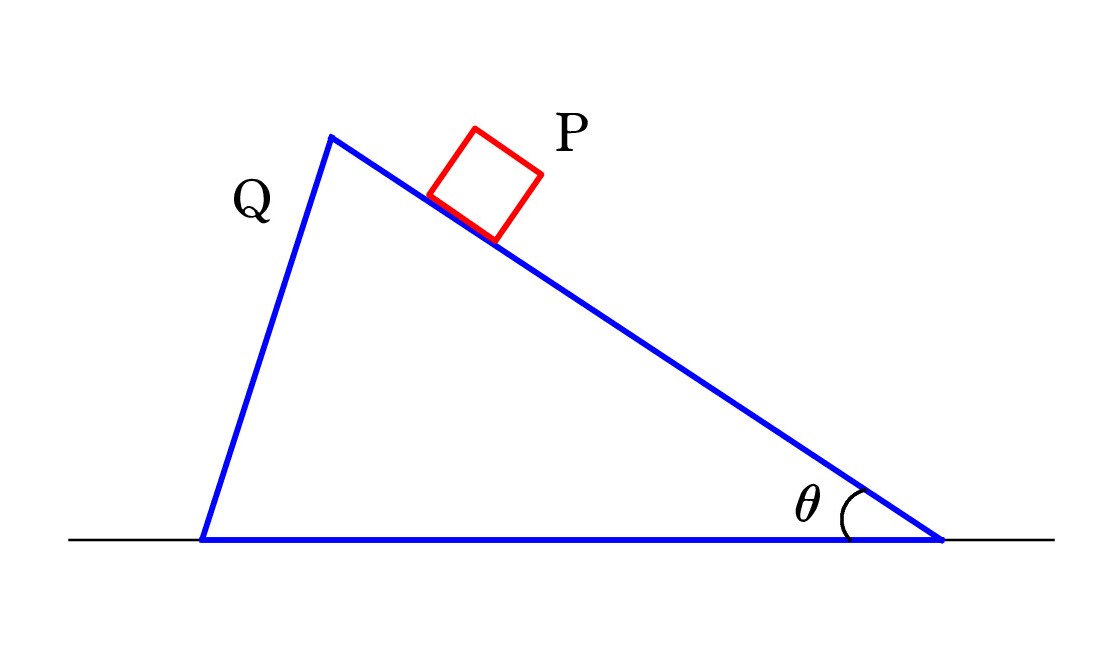Q1.　Ｐが三角柱Ｑの上を滑り降ります。摩擦はどこにもなく、Ｑは水平床上を左へ動きます。ＱがＰに及ぼす垂直抗力Ｎのする仕事 Ｗ が試験で問われました。
「垂直抗力は仕事をしない」と思いますが・・・


A.　固定面上を滑るのなら、垂直抗力は仕事をしません。曲面上でもいいです。
　たえず、N と移動の向きが直角をなすからです。
　なお、摩擦のあるなしは関係ありません。

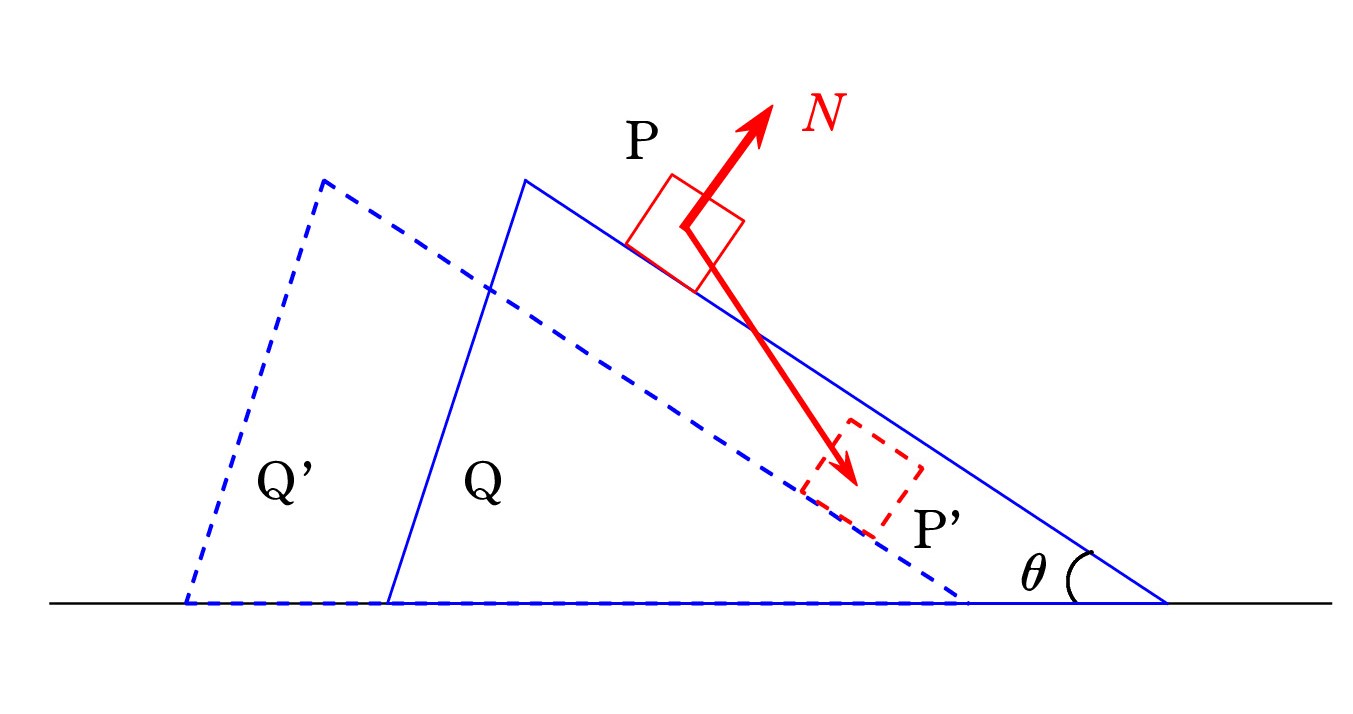
　いまの場合、三角柱Ｑが動きます。図を見て下さい。
　点線が後の状態 P‘ と Q’ です。
　N の向きと移動の向き（ＰＰ‘の向き）は直角ではありません。　W は０ではないのです。
　図から　Ｗ＜０　と分かります。




Q2.　N ＝ ｍｇcos θ ですから、あとは移動したＰＰ‘ を調べれば、Ｗ が求まるのですね。


A.　残念ながら、Ｎ は ｍｇcos θ ではありません！　多くの人が間違えます。
　直線運動では、運動に垂直な方向では力がつり合います。固定斜面なら、斜面に垂直な方向で力がつり合い、N ＝ ｍｇcos θ となります。しかし、今の場合、Ｐ→Ｐ‘ という運動の向きは θ 方向ではないからです。

　Ｎ は運動方程式から決めることができます。「森」の力学の問題 22 で扱っています。　ただ、質問の内容からすると、保存則で扱っている問題と思います。そうなら、後の状態でのＰの速さが分かるはずで、「非保存力の仕事 ＝ 力学的エネルギーの変化」という定理で Ｗ が求まります。「 Ｗ ＝ Ｐの(運動エネルギー＋位置エネルギー) の変化 」ですね。

　２つの物体が力を及ぼし合いながら運動するときは、運動方程式で攻めるか、保存則で攻めるかの二大戦略 です。　前者なら、加速度という運動の詳細がつかめるので、垂直抗力の仕事など尋ねないはずです。




Q3.　確かに、試験問題は 運動量保存則と力学的エネルギー保存則とで話が進んでいます。　Ｗ の求め方も納得しました。
　でも、その後で気付いたのですが、力学的エネルギー保存則が適用できるためには、非保存力の仕事がないことが条件 だったはずです。垂直抗力は非保存力です。 Ｗ≠０ では 矛盾そのものではないでしょうか？


A.　Ｗ≠０ のため、Ｐ単独では 力学的エネルギー保存則が成り立ちません。
　ＰとＱの物体系なら 大丈夫なのです。
　もう一つの垂直抗力（Ｎの反作用）がＱに仕事 Ｗ‘ をしています。そして、全体としての仕事は 0 、つまり、Ｗ＋Ｗ’＝０ なのです。　したがって、物体系としては 力学的エネルギー保存則が成立しています。

　そもそも、「垂直抗力の仕事が…」などとは ふつうは考えないのです。
　摩擦がないので、関連するエネルギーは 運動エネルギーと位置エネルギーだけですね。　そこで、物体系では 力学的エネルギー保存則が成り立つはずと思って、適用してください。 エネルギーに注目する観点 が大切 です。　堅苦しく言えば、関連するエネルギーをすべて考えれば、保存するという（一般的な）エネルギー保存則 に基づいての判断です。

　上の Q＆A で扱った 糸で結ばれた２物体の運動でも、張力の仕事には目を向けず、糸はエネルギーを持たないからと、サラッと物体系での力学的エネルギー保存則に入ります。

Q4.　仕事にこだわるようで、申し訳ありませんが、垂直抗力の仕事の和が０になること、つまり、Ｗ＋Ｗ’＝０ となることは示せますか？


A.　示せます。　次回までの課題にしましょう。
　入試で問われることはないので、興味と時間のある人だけが考えてください。

　ちなみに、２つの垂直抗力は 物体系で見れば 内力であり、「合力が０となるので、仕事も０だから」とか、「内力の仕事の和は０になるから」というのは、予備校の講師でも犯しそうな 誤りです。
　また、「物体系としては 力学的エネルギー保存則が成り立つから」というのは、通常の議論では認められますが（先ほど触れた エネルギーに注目する観点 からの帰結として認められますが）、今の議論では 本末転倒です。

　　ヒント


　　　　　・・・・・・・・？・・・？・・・？・・・？・・・？・・・・・・・・



Q5.　考えてみましたが、導出できませんでした。
　答えを伺う前に、「内力の合力は０となるので、仕事も０だから」や「内力の仕事の和は０になるから」という答えでは なぜ いけないのでしょうか ?


A.　確かに、内力の和なら、作用・反作用の法則 によって０ になります。
　しかし、力のほかに変位が絡む 仕事 は違います。　２つの物体の変位が異なれば、話は単純ではありません。

　「合力が０となるので 仕事も０」や「内力の仕事の和は０」という主張への反例としては、ＰＱ間に動摩擦がある場合が挙げられます。　内力で合力は０ですが、その仕事の和は０になるどころか、負になります。　その分だけ力学的エネルギーが減少し、摩擦熱に変わります。
　「森」の問題 16 の追加設問 Q が参考になるでしょう。

Q6.　なるほど、ＰＱ間に動摩擦があれば、相互に働く内力ですが、摩擦熱が発生しますね。　摩擦熱 と 動摩擦力の仕事 は 表裏の関係でした。
　それでは、同じく内力である垂直抗力について、仕事の和が０になることの説明をお願いします。


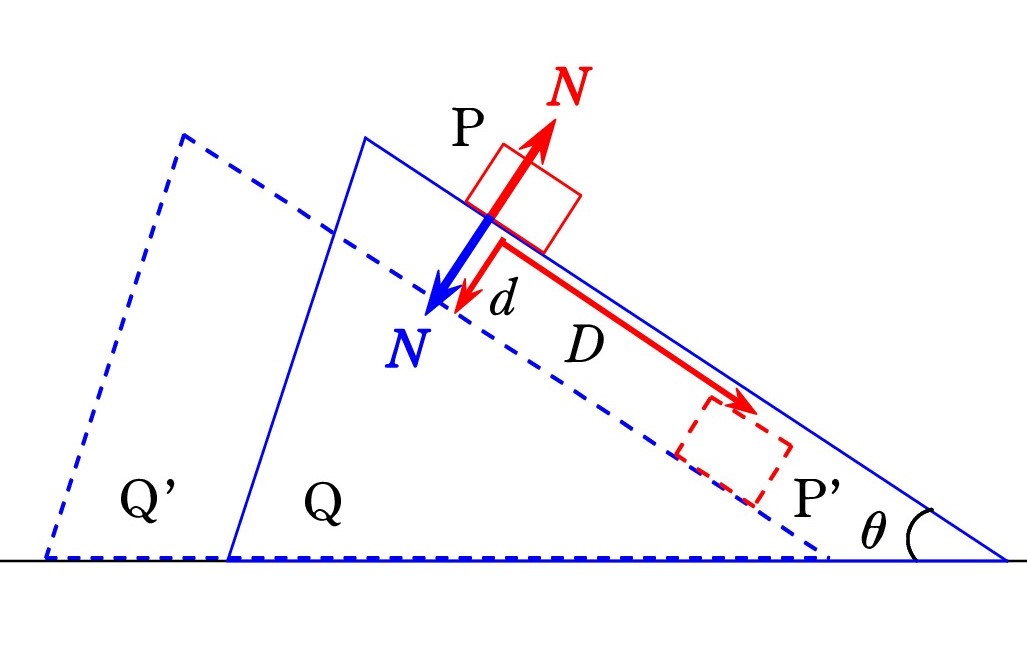A.　Ｐ の変位を 垂直抗力 Ｎ (赤矢印) の方向のｄと 直角方向のＤに分解すると、Ｄによる仕事はなく、
　　　　Ｎ の仕事は 　　Ｗ ＝ −Ｎｄ
　一方、Ｑには Ｎ の反作用 Ｎ(青矢印) が働きます。力の向きへの変位は やはりｄなので、
　　　　反作用Ｎの仕事は　　Ｗ’＝ ＋Ｎｄ
　したがって、　Ｗ＋Ｗ’ ＝０
　Ｐ と Ｑ が接触しているため、接触面に垂直な方向での移動距離ｄが共通になっていることがポイントですね。
　
　ベクトルの内積を用いる方法は 別記 しておきます。ここに掲載するほどのことでもないので。（ついでに、動摩擦力の仕事の和は負になることも確認しています。）




Q7.　Ｗ＋Ｗ’ ＝０ だと、物体系として力学的エネルギー保存則が成立することが示せますか？


A.　示せます。　まず、定理「非保存力の仕事 ＝ 力学的エネルギーの変化」をＰとＱに対して適用してみると、
　　　　Ｐ ：　Ｗ ＝ Ｐの力学的エネルギーの変化　……(a)
　ＱにはＮの反作用と床からの垂直抗力Ｒの２つの非保存力が働いています。　そこで、
　　　　Ｑ ：　Ｗ‘ ＋ Ｒがする仕事Ｗ_床 ＝ Ｑの力学的エネルギーの変化　……(b)
　Ｗ_床＝０であり、　(a)＋(b) とすると、
　　　　　　　　　　Ｗ＋Ｗ‘ ＝ ＰとＱの力学的エネルギーの変化
　Ｗ＋Ｗ’ ＝０ なら、ＰとＱ全体の力学的エネルギーが変化しない、つまり、保存則が成立しています。

　導き方をたどると、上の定理は、一つの物体だけでなく、物体系に対しても成立していることが分かります。

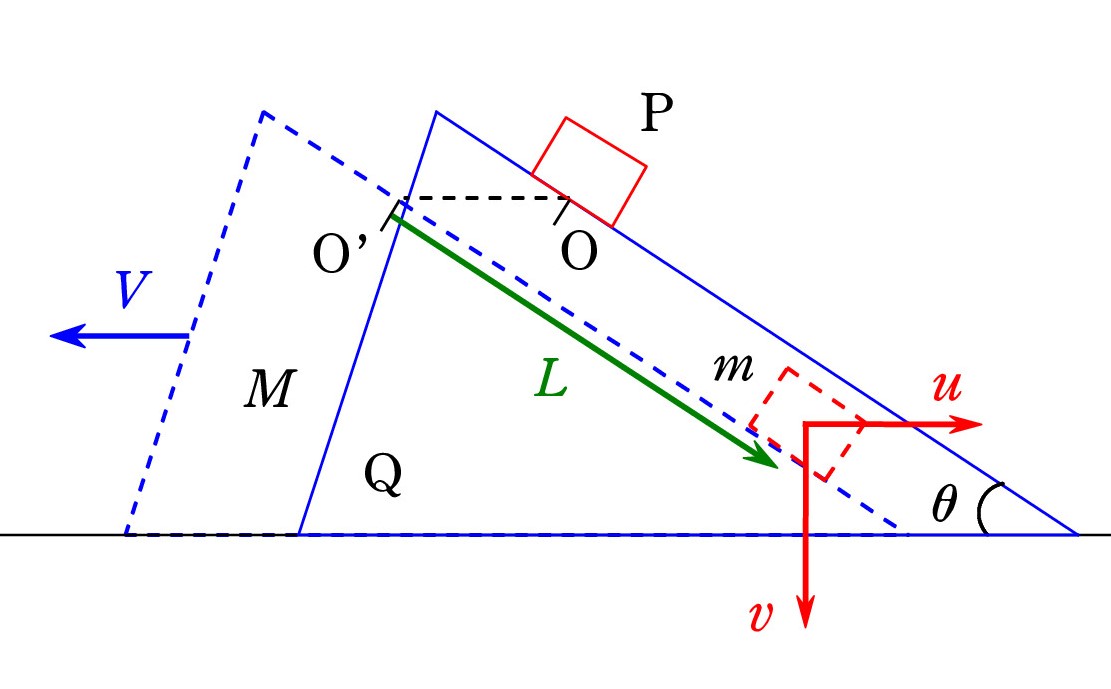Q8.　保存則を用いて連立方程式を立てたのですが、上手く解けません。

　はじめ全体は静止しており、質量ｍのＰが斜面に沿ってＬだけ降りたときの、速度の水平成分と鉛直成分の大きさを、ｕとｖとし、質量ＭのＱの速さをＶとします。
　水平方向には外力がなく、運動量保存則が成立します。　はじめ静止していたので、
　　　　　　　　ＭＶ ＝ ｍｕ　　……�@
　物体系についての力学的エネルギー保存則は、
　　　　　　　　ｍｇ・Ｌsin θ ＝ ｍ(u²＋ｖ²)/２ ＋ ＭＶ²/２　　……�A
　左辺が失われた分で、右辺が現れた分 です。　　Ｐの位置エネルギーが減少した分だけ、２物体の運動エネルギーになっています。　u²＋ｖ² は 三平方の定理から Ｐの速さの２乗です。

　距離Ｌは与えられているので、未知数は ｕ、ｖ、Ｖ の３つですが、保存則を用いても �@ と �A の２つしか式がなく、連立方程式が閉じない のです。


A.　仕事の話は重苦しく、ぬかるみを歩む感がありましたが、保存則になれば、視界が開け、スッキリします。

　力学的エネルギー保存則の立て方については、その通りで、付け加えることがありません。

　運動量保存則についていくつかふれておきたいことがあります。
　今の場合、運動量保存則は水平方向に限られるという認識は大切 です。　式 �@ は、静止から始まっているので水平方向の全運動量が０であり、Ｐが右に動けば Ｑは左に動くはず と見通してのもの――と思いたいですね。　Ｑの動きが伏せられても大丈夫なように。
　右向きを正として、０＝ Ｍ・(−Ｖ) ＋ ｍ u とする人もいるでしょうが、�@ の方が理解が深い感じがします。　正の向きの指定も不要ですし。

　もしも、Ｖ、u が 符号を含む速度成分なら、０ ＝ ＭＶ ＋ ｍ u　としなければならないことも意識してください。「速さ」と「速度」の違いは、運動量保存では決定的 です。　　動きが読めないときは「速度」あるいは「速度成分」を用います。そして、答えの符号から運動の向きを判断します。


　さて、質問の、連立方程式を完成させるためのもう一つの式は、入試でも取り上げられ、難問で大きな点差がつくものです。　ぜひ考えてほしいので、解答は次回にしましょう。

　　ヒント








　　　　　・・・・・・・・？・・・？・・・？・・・？・・・？・・・・・・・・







　　　　　　　　　　 ここは「解答」がすぐに目に入らないように用意した空白です



　　　　　　　　　　　　　　 自分なりの解答は用意できましたか？






　　　　　・・・・・・・・？・・・？・・・？・・・？・・・？・・・・・・・・










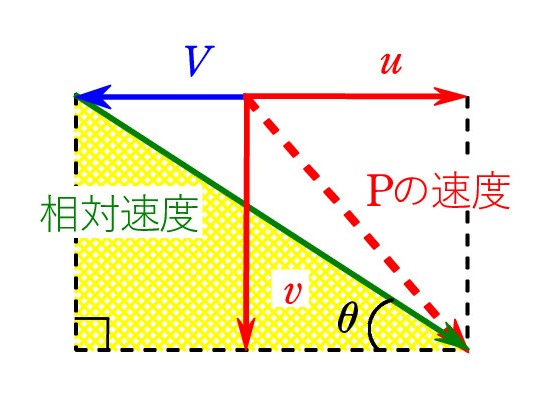A.　「もう一つの関係式」を出すには、Ｐが斜面に沿って滑り降りるという点を生かします。
　Ｑから見れば、Ｐは斜面方向、つまり、水平から角度 θ の方向に動きます。　相対速度がその向きになる ということです。
　Ｐの速度(赤点線)からＱの速度を ベクトルとして引いたものが相対速度です。

　黄色の直角三角形から　ｖ＝（Ｖ＋ｕ）tan θ　・・・�B

　これで 連立方程式 �@〜�B が解けます。




Q9.　初めの質問に戻ると、垂直抗力の仕事 Ｗ は
　　Ｗ＝Ｐの力学的エネルギーの変化＝｛ｍ(ｕ²＋ｖ²)/２＋０｝−（０＋ｍｇ・Ｌsin θ）
で求められる ということですね。


A.　そうです。　ただ、今までの話を思い出してもらえば、もっと簡単な計算法があります。　　Ｗ＋Ｗ’ ＝０ だったでしょ。　Ｑ に注目して、
　　　　　　Ｗ‘ ＝ Ｑの力学的エネルギーの変化 ＝ ＭＶ²/２−０
であり、　Ｗ ＝−Ｗ’ とすると 早いのです。
　Ｗ_床＝０ と Ｑは位置エネルギーの変化がないことを考慮に入れています（式(b)参照）。

　仕事はエネルギーのやり取りを表しています。 上の結果は、P から Q に ＭＶ²/２ だけエネルギーが譲り渡されたということです。
　はじめから、Q が得た運動エネルギーに目を向けていれば、定理を持ち出すほどのこともなかったとも言えます。


　今回はずいぶん長い応答になりましたが、大切なのは保存則の理解であり、式 �@ と �A が立てられること です。
　式�Bはナルホドと思ってほしいものです。そして、これからは 図を描き立式できるようにしてください。　(相対)変位ベクトルや (相対)加速度ベクトルでも同様に成り立ちます。　前者については、「別記」の 図 を見て下さい。
「Ｑから見れば…」つまり「Ｑの上に立ってＰの動きを見れば…」という見方が大切 です。

　話の始まりは仕事でしたが、仕事は 尋ねられれば 考える という程度でよいでしょう。




Q10.　相手の Q に目を向けると計算が楽という話は、２物体が衝突したときの 力積の計算でも出会ったことがあります。　力積＝運動量の変化 で求めるのですが、衝突の際の 力積は、作用・反作用によって 同じ大きさで逆向き なので、はじめ静止していた相手の物体を利用しました。

　ところで、Ｑ の表面が曲面でも、垂直抗力の仕事の和が０（ Ｗ＋Ｗ’＝０）は成り立つと思ってよいでしょうか。　微小区間に分ければ、区間ごとは斜面で、全体は斜面の集合ですから。


A.　その通りですね。　結局、物体系なら、垂直抗力の仕事は考えなくてよい ということです。

　摩擦がなければ、物体系に対して力学的エネルギー保存則を堂々と用いてください。

Q11.　最後に、確認しておきたいことがあります。　法則と定理の関係です。
　「 運動方程式」→「仕事＝運動エネルギーの変化」→「非保存力の仕事＝力学的エネルギーの変化」という順序で導出されていて、非保存力の仕事が０なら、力学的エネルギー保存則が成立するという理解でよいでしょうか。


A.　正しいです。　運動方程式 が法則で、その他が定理ですね。

　「仕事＝…」の左辺は物体に働くすべての力のする仕事の総和で、そのうち、保存力の仕事を位置エネルギーに格上げして、右辺に用意した形が「非保存力の仕事＝・・・」です。
　この関係から、非保存力の仕事が０のとき、力学的エネルギー保存則 が成立することが分かります。　重要さを強調して力学的エネルギー保存の法則と呼んでいますが、位置づけとしては、証明できる定理です。

　これに対して、（一般的な）エネルギー保存則 は証明しようのない、まさに法則です。　無からエネルギーを生じさせようとする試み（永久機関の発明）がすべて失敗と化し、その事実が、累々たる瓦礫の山が、法則を支える強力な根拠となっています。




Q12.　そうすると、物体系の力学的エネルギー保存則を用いて（運動量保存則と式 �B も含めて）、u、v、V を求めた後で、式(a)や(b)で垂直抗力の仕事 Ｗ を求めるのは「先祖返り」というか、話が逆流しているように思いますが・・・


A.　まったくその通りで、物理としては「問題のための問題」と言ってもいいでしょう。　Ｗ 自体に大した意味はなく、Ｗ を求めても次につながるわけではないので。
「非保存力の仕事＝力学的エネルギーの変化」という定理は、本来は、非保存力の仕事 が直接分かる場合に、物体の 後の速さを求めるためのものです。
　ただ、入試としては、この定理が身についているかどうかを試す という意味があります。
また、垂直抗力は仕事をしない と決めつけている人に 警鐘を鳴らすという学習効果もあるでしょう。


　繰り返しになりますが、いろいろな問題に出会ったとき、運動方程式と保存則こそ二大戦略として意識すべきものです。それぞれに強みと弱みがあります。

　三角柱Ｑの上をＰが滑る今の問題では、運動方程式なら、Ｐの加速度（の水平・鉛直成分）が一定であることが分かります。したがって、静止から動き出したＰは床に対して等加速度直線運動をします。上の図では赤点線の方向ですね。　そして、位置や速度の時間変化も計算できます。

　一方、保存則では直線運動かどうかさえ すぐには分からないのです。ですが、Ｑの面が斜面ではなく、曲面であっても扱えるというのが保存則の強みです。
　曲面の場合でも、式 �@、�A は成り立ちます（摩擦はなく、初め静止として)。
ただ、Ｌｓｉｎθ は 滑り降りた高さｈに置き換えます。　また、式 �B は意味を失うと思われそうですが、ｈ 降りた点で 曲面の接線が水平となす角度を θ とすればＯＫです。
　実際には、曲面に続く水平面に降りてきたときが扱われるのがふつうで、ｖ＝０で 未知数は u とＶの２つになり、�@、�A の連立で解ける問題が殆どです。 水平面でなくても、接する面が水平ならよく、円筒面の最下点などが該当します。


　では最後に、三角柱Ｑの場合に戻って、保存則の理解に関しての問題です。

　P と 三角柱Q および 床 の間に 次のような摩擦がある場合、式 �@、�A、�B のそれぞれは成り立つかどうか。 〇、× で答えて下さい。　初め全体は静止し、u、v、V は各場合に応じた正しい値とします。

　(a)　P と Q の間にだけ 摩擦がある場合

　(b)　Q と 床 の間にだけ 摩擦がある場合

　(c)　P と Q の間、Q と 床 の間、共に 摩擦がある場合
　　　　　　 　　　　　　　　　　　　　　　　　　　　　　　　解答（※�V※）は最後に

Q13.　すみません！　　あと一つ、解けない設問がありました。
　Ｐが三角柱Ｑに沿ってＬ滑り降りるまでにＱが移動した距離Ｘが問われています。
　これも保存則の考えで解けるのでしょうか？　無関係のように思えますが・・・


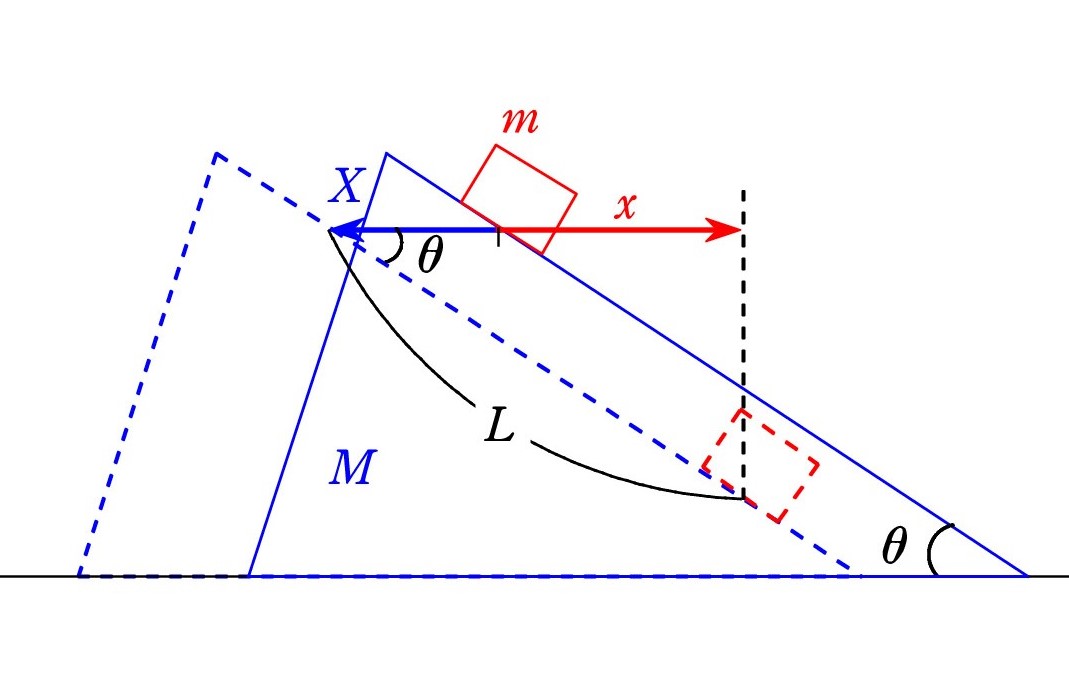A.　運動量保存則で解決できます。　水平方向での保存を表す式 �@ より　u / V ＝ M /ｍ (＝ 一定)　となり、速さは質量の逆比になっています。速さは時間とともに変わりますが、比が一定であるため、水平方向でのＰの移動距離ｘとＱの移動距離Ｘも同じ比になり、
ｘ/Ｘ ＝ Ｍ/ｍ です。　（ていねいな確認は下記（＊））
もちろん、静止から始まっているという条件付きです。
　これからは 移動距離の比も質量の逆比 ということまで 直ぐにつなげられるように。　　速さから距離につなぐのは違和感がないでしょう。

　今の場合、ＰとＱが水平方向に離れた距離は ｘ＋Ｘ＝Ｌｃｏｓθ なので、質量の逆比で分配し、ｘ＝Ｌｃｏｓθ・Ｍ/(ｍ＋Ｍ)であり、Ｘ＝Ｌｃｏｓθ・ｍ/(ｍ＋Ｍ) となっています。


　（＊）　a ＝ Ｍ/ｍ とおくと、u ＝ aＶ であり、微小時間�凾狽ﾅの移動距離を集めて
　　　　　　　　ｘ＝Σ u�凾煤＜ｰ a V�凾煤� a Σ V�凾煤� aＸ
　　　　　（ 積分の形にするとスマートに　　�� → ∫　　�凾煤ｨ dt　　　u、Ｖ は時間の関数 ）
　



Q14.　思い出したのですが、このような場合、全体の重心位置は不動だったと思います。この知識を活かすことはできませんか。


A.　できますが、それも元は運動量保存です。　ていねいには「運動量保存則が成り立つときは、重心は等速度で動く」という定理ですね。　いまの場合は、初め全体が静止していたので、重心Ｇは静止し続けます（エッセンス(上)ｐ66(新版 p67,68)）。　ただし、運動量保存が成り立つ水平方向 についてです。
　Ｐが下がるので、Ｇは下へは移動しています。　結局、Ｇは鉛直下向きに動いています。
　以下は、重心が不動となっている水平方向についての話です。

　水平右向きに x 軸を取り（座標原点はどこでもよい）、初めのＰ、Ｑの重心位置をｘ_m、ｘ_M とおくと、全体の重心ｘ_G は、公式より、
　　ｘ_G＝（ｍｘ_m＋Ｍｘ_M）/（ｍ＋Ｍ）＝｛ｍ(ｘ_m＋ｘ)＋Ｍ(ｘ_M−Ｘ)｝/（ｍ＋Ｍ）
　最後の式は、Ｐが右にｘ移動し、Ｑが左にＸ移動したときの重心位置を表しています。
　式を整理すれば、ｘ_m や ｘ_M は消えて、　 ＭＸ ＝ ｍｘ
　あとは、ＰとＱが水平方向に離れた距離 Ｘ＋ｘ＝Ｌｃｏｓθ　と連立させればいいでしょう。

　重心は重力のモーメントに関わっていました。　重心が動かないことは重力のモーメントが変わらないことです。
　ｍ が右にｘ 移動すれば、ｍｇｘだけ時計回りモーメントが増えるので、Ｍは左にＸ移動してＭｇＸだけモーメントを減らし、全モーメントを変えないようにすればよい――そう考えれば、ＭｇＸ＝ｍｇｘ　つまり　ＭＸ ＝ ｍｘ は即座に書けます。

　シーソーを思い出してもよいでしょう。　二人が乗ってつり合っているときの重心はシーソーの支点にあります。　左側の大人（Ｍ）が Ｘ 左に寄り、右側の子供（ｍ）は ｘ 右に寄って新たなバランスをとるとき、重心は移動せず、ＭＸ ＝ ｍｘ です。


　Ｑが三角柱でなく、曲面を持った台であっても、式 �@ 　ＭＶ ＝ ｍｕ　は成り立ちます。　したがって、Ｐが台上で水平方向に移動した距離が与えられれば、Ｐ、Ｑが床に対して水平方向に動いた距離は、質量の逆比で分配して求められる ということです。
　もちろん、床に摩擦はなく、全体ははじめ静止しているという条件を忘れないようにしてください。　ＰＱ間の摩擦はあっても構いません。

　滑らかな床上に板を置き、その上を人が歩く――という設定も同じことです。　動摩擦ではなく静止摩擦で歩くのはいいですね。　摩擦力が一定でなくてもいいのも理解してほしいことです。
　30kg の板上を 60kg の人が板に対して 120cm 移動したとき、人が床に対して進んだ距離はいくらですか？


　　　　　・・・・・・・・？・・・？・・・？・・・？・・・？・・・・・・・・



Q15.　質量比が 2：1 ですから、120cm を分配して 40cm です。板は 80cm 後ろに下がっています。「 重い物体の方が動きにくい 」というチェックもしました。
　人はゆっくり静かに歩く必要があるかと思っていたのですが、歩き方はどうでもいいんですね ！
　でも、いきなりこの問題に出会ったら、途方にくれます。　運動量保存の世界の重要さが実感できます。

　重心の話は、重力のモーメントでの説明のおかげでスッキリしました。　変化した分に注目すると早いのですね。　三角柱Ｑの重心がどこにあるかとか、全体の重心がどこかなど気にしなくてすみます。
　重心の公式を用いるにしても、変化分は ｍｘ＋(−ＭＸ) で、これを０とおけばすみそうです。


A.　その通りです。　「変化した部分で考える」はいろいろな場面で活用できます。

　力のつり合いでも、状況が変わって新たなつり合いに移れば、変化した部分だけでつり合いを考えると早い です。　水に浮いている木の上におもりを載せると、木が少し沈みますが、 (浮力の増加分)＝(おもりの重力） として扱いたいです。
　シーソーに何人かが乗ってつり合っているとき、両側に一人ずつさらに乗せて つり合わせたいなら、新たに乗る二人についてモーメントのつり合いが取れればＯＫです。

　エネルギー保存則で「 失われた分 ＝ 現れた分 」としていたのも 同類の考え方です。

　物体を力のつり合い位置からｘずらして、Ｋｘ の復元力が生じるときに単振動が起こります（Ｋ：定数）。　このとき、ｘ によって変化する力だけを追うと手っ取り早いです。
　たとえば、滑らかな斜面上に置かれたばね振り子なら、ｘ によって変わるのは ばねの弾性力で、ｋｘ だけ変わりますし、それが合力で、元へ戻そうとする復元力です（ｋ：ばね定数）。だから、単振動するとすぐに分かります。
　ばね振り子が単振動することは 誰もが知ってしまっているので、あまり感動はないかもしれませんが、知っていることと 理解していること との間には大きな差があります。



　今回扱ったＰと三角柱Ｑの問題はすでにハイレベルですが、もう一段階 難度を up したいとき、出題者は次のように問いかけます。

　「ＰをＱ上で滑らないようにし、全体を速さ U₀ で床上を右に運動させる。そして、Ｐを自由にした。　Ｑ上をＬ滑り降りたときの、Ｐ、Ｑ それぞれの速度(成分)を求めよ。」

　どう対応しますか ？


　　　　　・・・・・・・・？・・・？・・・？・・・？・・・？・・・・・・・・



　U₀ で動く観測者を想定します。　その人にとっては、静止していたＰ、Ｑ が動き出したという、今までの問題に戻っています。
　u、ｖ、Ｖ を求め、あとは 床に対する速度に変換すればよく、観測者の速度を加えて、Ｐの水平成分は U₀ ＋ u 、鉛直成分は ｖ 、 Ｑ は U₀ ＋(−Ｖ)＝ U₀ −Ｖ ですね。　右向きと鉛直下向きを正としています。
　Ｐを自由にした後も観測者は U₀ で動き続けていること、等速度系であることが大切です。
　「等速度系は慣性系」であり、保存則が用いられます。　もちろん、運動方程式も。
　力学に限らず、物理法則のすべてが用いられます。

　はじめ、全体を左向きに U₀ で動かしておくと、難度はさらに少し up します。考えにくいので。
　でも、ここまで聞いた段階では大したことはないでしょう。

　　　　　・・・・・・・・？・・・？・・・？・・・？・・・？・・・・・・・・


　Ｐ の水平成分は −U₀ ＋ u で、鉛直成分は ｖ、そして、 Ｑ は −U₀ −Ｖ ですね。

　はじめから Ｐを自由にし、Ｐ、Ｑ 共に U₀ の初速度を水平に与えても 同じことです。
　u、ｖ、Ｖ を手にしていても、等速度系の利用は気づきにくく、新たに連立方程式を立てて、解こうとする人が殆どです。

　このように、典型的な状況設定に「等速度系という要素」を加えると、難度が上げられます。　出題者の「奥の手」と言ってもいいでしょう。



　　　　　　　　　　ここで この Dialogue は 一応 終わりです。

　『探究の旅に出よう』の「疑義のある出題・・・保存則と時間」で発展的な内容を扱っています。

Q.　「エッセンス」によれば、鉛直方向で２物体が衝突するとき、瞬間的な衝突であれば、運動量保存則を適用してよいとのことです（（上）ｐ59）。もちろん、衝突の直前と直後に関してです。
　しかし、適用できる理由は、瞬間的な衝突かどうかではなく、衝突時の２物体間の垂直抗力が重力に比べて圧倒的に大きいため、重力が無視できるからではないでしょうか。
　衝突時の垂直抗力は撃力と呼ばれる大きな力です。外力である重力が無視できれば、水平方向での衝突と同じになります。


A.　実は、私も昔はそのように考えていました。　しかし、垂直抗力が撃力でなくても、衝突時間さえ短ければ、運動量保存則が近似的に成り立つのです。垂直抗力は作用・反作用の力なので、力積全体としては消えてしまい、衝突前後の全運動量の違いは重力の力積の分だけになってしまうからです。　以下、確認してみます。

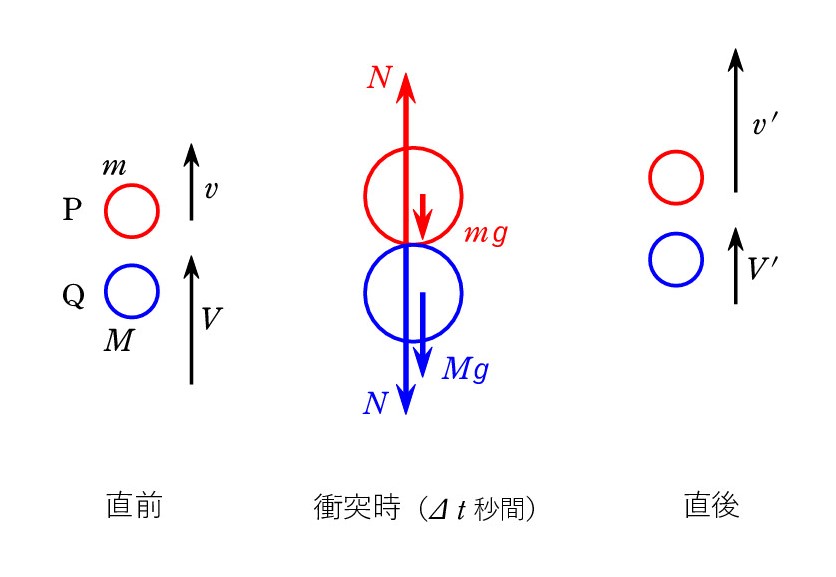　P の質量を ｍ、衝突直前の速度をｖとし、Q の方は M、V とします。衝突直後の速度をｖ‘、Ｖ’ とします。　そして、衝突時の垂直抗力の大きさを N 、衝突時間を�凾狽ﾆし、上向きを正として　「力積 ＝ 運動量の変化」を適用します。

Ｐ について、
　Ｎ�凾煤{（−ｍｇ�凾�) ＝ ｍｖ‘− ｍｖ　…�@　
Ｑ について、
　−Ｎ�凾煤{（−Ｍｇ�凾�) ＝ ＭＶ’− ＭＶ …�A　
　�@ ＋ �A より、　　　−（ｍ＋Ｍ)ｇ�凾� ＝（ ｍｖ‘＋ ＭＶ’）−（ ｍｖ ＋ ＭＶ ）

　右辺は衝突前後の全運動量の差です。その差は N に関係なく、重力の力積の分だけです。したがって、�凾煤ｨ０ で運動量は保存します。
　なお、図の速度の矢印の向きや長さは適当です。Ｐが落下して上昇中のＱと正面衝突してもいいです。「上向きを正」にしたので、速度の矢印は上向きに描いておくと 何かと間違えません。

　念のためですが、重力は一定なので �凾煤ｨ０ でその力積は０に近づきますが、撃力 Ｎ の方は衝突時間が短くなると大きくなるため、撃力の力積 Ｎ�凾� は０に近づきません。撃力 Ｎ のお陰で速度は衝突で瞬時に変わります。 �@では ｖ‘ は ｖと異なり、�AでのＶ’も Ｖと異なります。

　 運動量保存則の成立条件は物体系に対して「外力が働かない場合」ですが、近似的成立まで含めれば、「外力の力積が０とみなせる場合」です。　鉛直なばねに支えられている板上に落下した物体が瞬間的に衝突する場合は大丈夫ですが、人が板上にひざを曲げながら飛び降りるようなケースは �凾狽ｪ長く、運動量保存則は適用できません。「森」(上) の問題 33 も参考にしてください。

　運動量保存則が成立するかどうか、懸念がある場合には、定理「力積＝運動量の変化」に戻って調べる・・・大切な姿勢ですね。　この定理は運動方程式から導いたもので、無条件に成立しています。　戻るべき関係を知っていることが大事で、言い換えれば、力学の構成を認識していることです。　「エッセンス」（上）ｐ93 (新版 p 95) に構成を記しています。












＃＃＃　Dialogue （対話）：　Q1 〜 Q23　＃＃＃＃＃

　　――――――　衝突　・　保存則　・　重心系　――――――



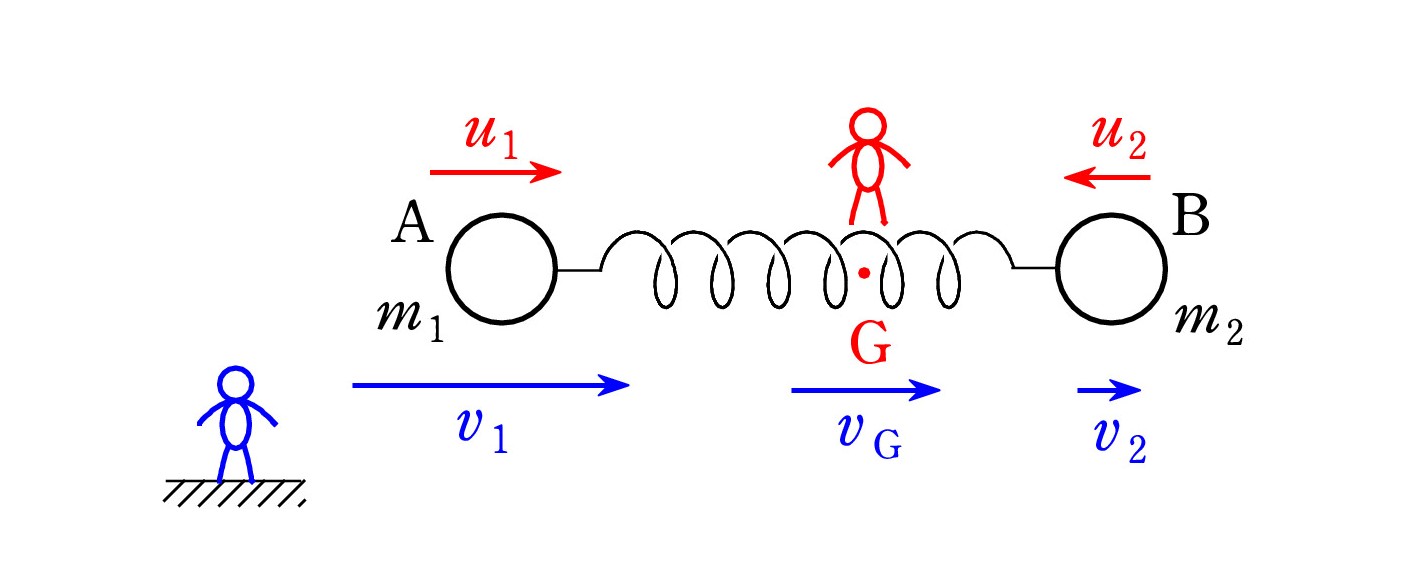
Q1.　「森」の力学の問題 37 では滑らかな水平面上での衝突が扱われています。まず、C が静止している A に弾性衝突します。 衝突直後 A は速度を得ますが、A と軽いばねでつながれている B は静止したままです。 ばねが縮み始めると同時に弾性力が生じ、B も動き出します。 衝突直後から、Ａ と Ｂ の重心 Ｇ は等速度 ｖ_Ｇ で動き、Ｇ に対して Ａ と Ｂ が振動を続けます。
　学校の先生によると、これは２物体の衝突モデルと見ることもできるとのことでした。 詳しく説明して頂けませんか。

　
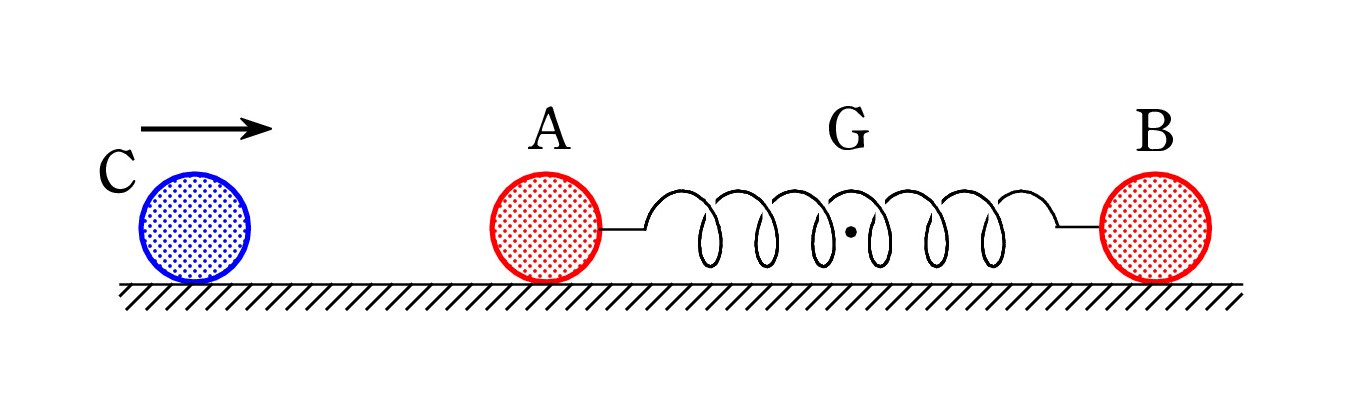
A.　「 A と ばね と B 」全体で一つの物体 X とみなせば、C と X との２物体の衝突です。運動量保存則が Ｃ と X の間で成り立ちます。 X の質量は Ａ と Ｂ の質量の和 M で、X の速度は ｖ_Ｇ です。　Ｃの速度と ｖ_Ｇ を用いて 反発係数の式を考えることもできます。
　C A 間が弾性衝突なので、エネルギー保存則（★）は、
　（衝突前の Ｃ の運動エネルギー）＝（衝突後の Ｃ の運動エネルギー）
　　　　　　　　　　　　　　　　　　＋（重心 Ｇ の運動エネルギー Mｖ_Ｇ²/２ ）
　　　　　　　　　　　　　　 　　　　＋（振動のエネルギー）
　振動のエネルギーには 弾性エネルギーも含めています。

　衝突モデルとしての意味は、衝突によって物体には振動が生じる ことへの理解です。　　現実には、Ｘ は一続きの弾性体であり、形は直方体でも球でもいいのです。 衝突で左端がへこみ、それが全体に伝わって、 Ｘ のように振動しながら ｖ_Ｇ で動くのです。『Ｑ＆Ａ エッセンス』 では、「ブルブル振動する」と表現しました。（次に転載）
　そして、振動のエネルギーは 物体内部の摩擦によって 熱に変わっていきます。 それが衝突で失われる力学的エネルギーですね。

• 『Ｑ＆Ａ エッセンス』

　入試問題としては、最初の Ｃ と Ａ の衝突の際、Ｂ は無関係であることに注意してください。　 重心 G が等速度で動く ことも大きなポイントです。
　問題 37 では Ａ と Ｂ の質量が等しいので、重心 Ｇ は 中点ですが、質量が異なるときは、逆比で内分 することになります。
　重心の速度は 重心座標の公式と同形になります（「エッセンス」（上）ｐ66 (新版 p 67) ）。 Ａ と Ｂ の運動量の和を質量の和で割った形です。　重心の運動量 Mｖ_Ｇ は Ａ と Ｂ の運動量の和に等しい とも言えます。　上で C と X の間で運動量保存則が成り立つと言ったのは、これに基づきます。






Q2.　上記の エネルギー保存則（★）は もっともらしい とは思います。　ただ、もう一つ スッキリしません。
　Ｘ に関して、 Mｖ_Ｇ²/２ で本当にいいのかどうか。　なにより、「振動のエネルギー」のところがブラックボックスに近い状況です。　これらは本来、A と B の運動エネルギーと 弾性エネルギーの和 になる部分です。


A.　高校の範囲をオーバーしますが、理解できるはずなので、以下、説明してみます。
　まず、重心系で見た、つまり、重心 G と共に動く観測者が見た、物体 A 、B の運動は 全運動量 ｐ_Ｇ が ０ であることを確認しておきます。
　ｖ₁、ｖ₂ を静止系での速度とすると、重心系での速度、ｕ₁，ｕ₂ は、
　　　　　　　ｕ₁ ＝ ｖ₁−ｖ_Ｇ　　　　　ｕ₂ ＝ ｖ₂−ｖ_Ｇ　　
　したがって　　p_Ｇ ＝ ｍ₁ｕ₁＋ｍ₂ｕ₂ ＝ ｍ₁ｖ₁＋ｍ₂ｖ₂−（ｍ₁ ＋ｍ₂)ｖ_Ｇ
　ここで　ｖ_Ｇ ＝ （ｍ₁ｖ₁ ＋ ｍ₂ｖ₂）/（ｍ₁＋ｍ₂） を用いると、　ｐ_Ｇ ＝０　（証明終り）

　「重心系 では、全運動量 は ０」ということです。　直線上の運動に限らず、ベクトルとして成り立ちますし、３個以上の物体系でも成り立つ定理です。
　２物体なら、重心系では速度の向きは必ず逆向き になります。今の場合は、A と B は重心 G に近づいたり、遠ざかったり、一瞬の静止をはさんで、たえず逆方向に動いています。一瞬静止するときも同時です。

　
　さて、静止系での A と B と ばね の力学的エネルギー Ｅ を ｖ_G などで表してみます。　自然長からのばねの伸び(あるいは、縮み)を ｘ とすると、
　　　　　　　Ｅ ＝ ｍ₁ｖ₁²/２ ＋ ｍ₂ｖ₂²/２ ＋ ｋｘ²/２
　　　　　 　　　＝ ｍ₁(ｖ_G＋ｕ₁)²/２ ＋ ｍ₂(ｖ_G＋ｕ₂)²/２ ＋ ｋｘ²/２
　　　　　　　 　＝（ｍ₁ ＋ ｍ₂)ｖ_G²/２ ＋（ｍ₁ｕ₁＋ｍ₂ｕ₂)ｖ_G
　　　　　　　　　　　　　　　　 ＋ ｍ₁ｕ_１²/２ ＋ ｍ₂ｕ₂²/２ ＋ ｋｘ²/２

　ここで　　ｍ₁ｕ₁ ＋ ｍ₂ｕ₂ ＝ ｐ_G ＝ ０　なので、
　　　　　　Ｅ ＝ （ｍ_１＋ｍ₂)ｖ_G²/２　＋ （ ｍ₁ｕ₁²/２ ＋ ｍ₂ｕ₂²/２ ＋ ｋｘ²/２ ）
　　　　　　　 ＝（重心 G の運動エネルギー Mｖ_G²/２ ）＋（ 振動のエネルギー）

　つまり、振動のエネルギーとは、重心系で見た A と B の運動エネルギーと弾性エネルギーの和です。　重心系における力学的エネルギーですね。

　上の計算は、「静止系での運動エネルギーの和 ＝ 重心 G の運動エネルギー Mｖ_G²/２ ＋ 重心系での運動エネルギーの和」が成り立つことを示している、と言った方が一般性があるでしょう。３次元で成り立つ関係です。
　気体分子運動論で 二原子分子の運動エネルギーを扱うとき、重心の分のほかに、重心の回りの回転による分を加えて考えるのは この関係があるからです。

Q3.　重心系が重視される理由の一端が分かった気がします。
「重心系では、全運動量が０で、２物体なら逆向き運動」なんですね。
　では、滑らかな水平面上で２つの物体が衝突し、斜め方向に飛び散るときも、重心系で見ると、２つは反対方向から来て、衝突し、反対方向に去って行くということでしょうか。


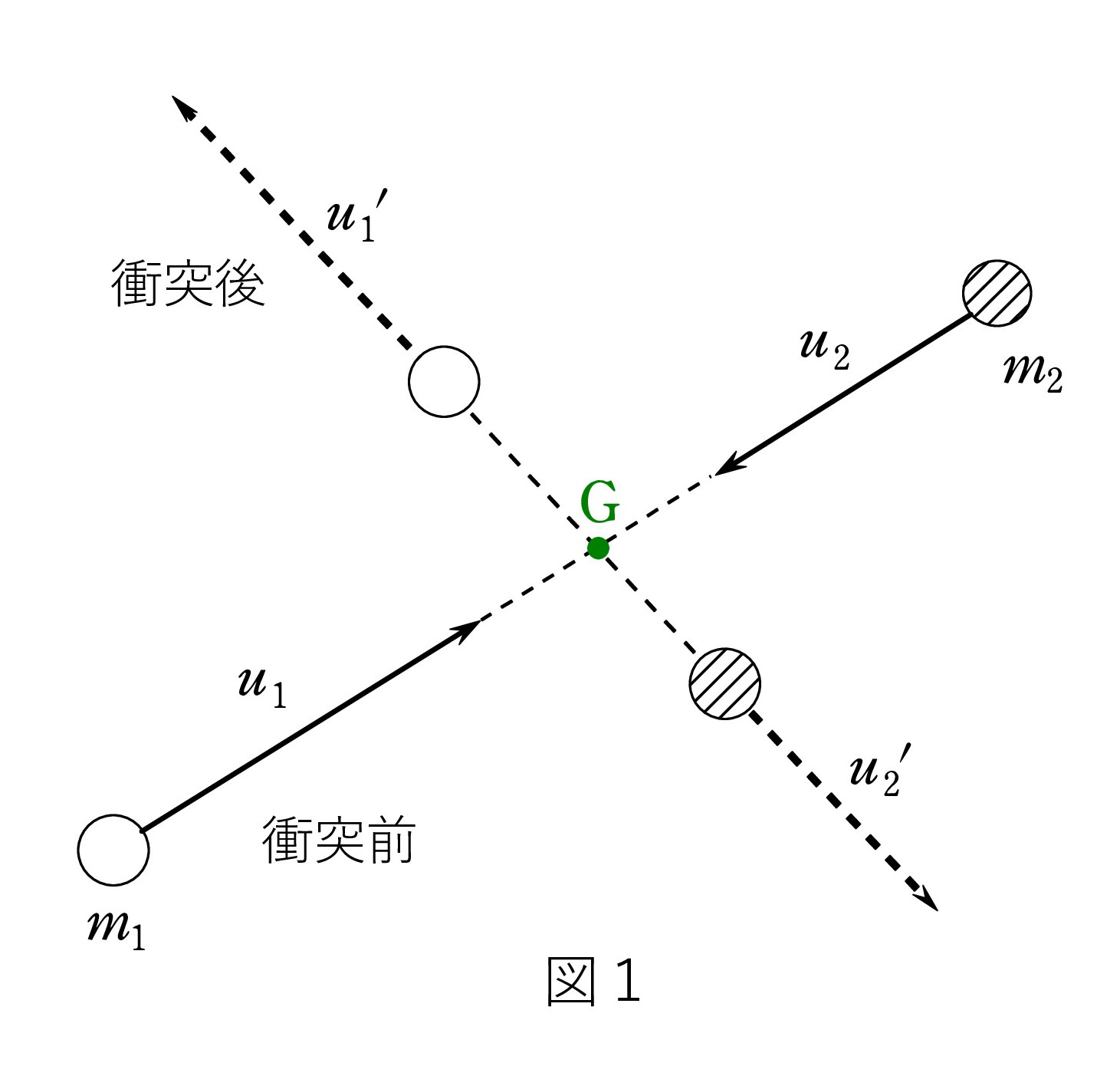A.　その通りですね。　重心系では、２つは直線上を向かい合ってやってきて、衝突し、また直線に沿って離れていきます。　ただし、前後の直線は一般には一致しません。正面衝突のときは一致しますが、一般には斜めに飛び散ります。
　このとき、２つの物体の速さの比が一定であることに注意してください。
　質量を m₁、m₂ とし、速さを u₁ 、 u₂ とすると、全運動量が 0 なので、　m₁u₁ ＝ m₂u₂
　よって、 u₁ / u₂ ＝ m₂ / m₁
　速さの比は質量の逆比 ですね。
　衝突後も同じことです。　（以下も u は重心系での速さ）




Q4.　重心系での速度とは、重心 G に対する相対速度のことですね。　平面上なので、ベクトルとしての引き算になるかと思います。


A.　そうです。　静止系での速度 v₁ 、v₂ と、重心系での速度 u₁ 、u₂ の関係を図で確認しておきましょう。　　（緑字はベクトル）
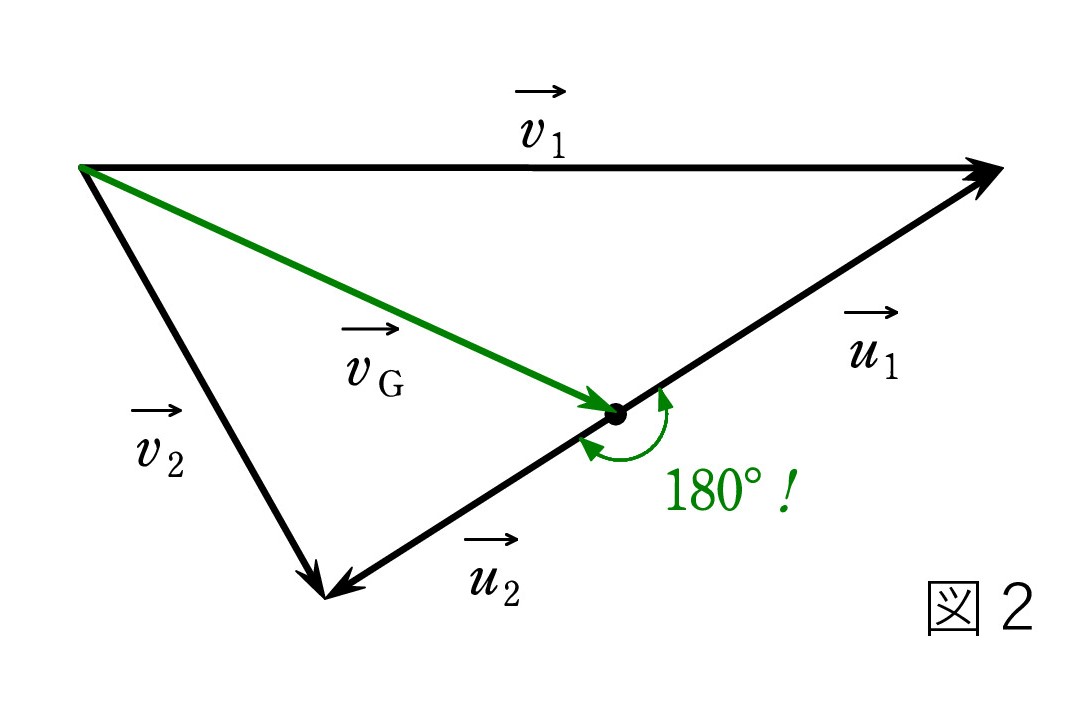　重心の速度を v_G とすると、u₁ 、u₂ は相対速度であり、右図のようになります。 u₁ 、 u₂ は正反対を向くことが大切です。
　図１の衝突前に合わせましたが、衝突後でも同様の図ができます。そのとき、v_G は不変であることにも注意してください。

　見方を変えると、v₁ と v₂ が与えられたとき、ベクトルの先端を結ぶ線分を、質量の逆比で内分した点を決め、根本とつなぐと重心の速度ベクトル v_G になる ということです。　また、 重心系での速度 u₁ と u₂ も現れています。　計算で出すのは手間がかかりますが、作図なら 驚くほど簡単なのが面白いですね。




Q5.　計算でも確認したいのですが・・・


A.　まず、重心の速度ですが、次の式で表されます。
　　　　　 v_G ＝ （ｍ₁v₁ ＋ ｍ₂v₂）/(ｍ₁＋ｍ₂）

　そこで、重心系での速度は、

　　　　　　 u₁ ＝ v₁ − v_G ＝ ｍ₂( v₁ −v₂ ) /(ｍ₁＋ｍ₂）　　・・・�@

　　　　　　 u₂ ＝ v₂ − v_G ＝ ｍ₁( v₂ −v₁ ) /(ｍ₁＋ｍ₂）　　・・・�A

　　　　　∴　u₂ ＝−(ｍ₁/ｍ₂) u₁ 　　・・・�B

　これは　 u₁ と u₂ は逆向きのベクトルで、長さ つまり 速さが質量の逆比になっていることを示しています。　また、 u₁ の式 �@ に現れた v₁ −v₂ は v₂ の先端から v₁ の先端へのベクトルで、 u₁ の向きに一致していることも読み取れます。

　また、�B を　ｍ₁u₁ ＋ｍ₂u₂ ＝ 0　と変形してみれば、「重心系での全運動量 ＝ 0 」が確認できます。
　



Q6.　今の話は 衝突の前に限らず、後でも成り立つことは理解できます。
　でも、衝突の前後で、なぜ、重心の速度 v_G が一定 と言えるのですか？


A.　滑らかな水平面上なので、外力がなく、運動量保存則が成り立ちます。すると、重心 G は等速度で動くのですが、論拠は 次のように「エッセンス」p66(新版 p67)に記しています。

　微分を用いていますが、微小時間�凾狽ﾌ間に座標が ｘ から ｘ ＋ �凾� になったとして導くこともできます(※)。

　重心の速度の式の導出も兼ねていることに注意してください。　重心の座標の公式からスタートしているので、同形になっています。　ｘ を ｖ に置き換えればよいのです。

　y 方向についても同様に導けるので、平面上の運動に対して成り立つことになります。　さらには、z 方向も同様で、空間内の運動でも大丈夫です。　そして、物体が３個以上あっても構いません。

　理解できない人も「運動量保存則が成り立つときは、重心 G は等速度になる」ことは知っておくとよいでしょう。　入試では、重心の速度の式を含めて、教えてくれるのがふつうですが。　なお、「 運動量保存則が成り立つときとは、物体系に外力が働かないとき」で、これは重要です。
　まとめると、「 物体系について、外力＝０」→「 運動量保存則」→「重心速度一定」 というつながりです。


(※) 変化後と変化前の x の関係式を書き、辺辺で引いて、　�凅_G ＝ ( m�凅_P ＋ M�凅_Q )/(m ＋ M)　を導き、両辺を�冲 で割ればよい。　�凅/�冲 ＝ v
　この例から分かるように、一次式の関係なら、変数が多くても、変数に�凾�付けた関係がそのまま成り立つ。　�� は微小でなくてよい。 ただし、定数項がある場合はなくす（辺辺の引き算で消える)。
　ｙ＝ ax ＋ b → �凉 ＝ a �凅 　は 時々出合う。

Q7.　重心系での衝突の図１に戻ります。　重心系では「速さは質量の逆比」なので、u₂ は u₁ で表せるということですね。
　すると２つの運動エネルギーの和 K が u₁ で表せることになります。　衝突後の運動エネルギーの和 K’ も u₁' で同じように表せるはずで、衝突では運動エネルギーの一部が失われるので、 K ≧ K’　よって u₁ ≧ u₁’ と言えると思います。
　同時に、 u₂ ≧ u₂’ も。


A.　そうです。　一応、計算でも確かめてみましょう。
　式変形のテクニック　ｍu²/2 ＝ (mu)²/2m　と、全運動量０による　m₁u₁ = m₂u₂　を用いて、
　　K ＝ m₁u₁²/2 ＋ m₂u₂²/2 ＝ (m₁u₁)²/2m₁ ＋ (m₂u₂)²/2m₂
　　　＝ (m₁u₁)²/2m₁ ＋ (m₁u₁)²/2m₂ ＝ (m₁u₁)²(1/m₁ ＋ 1/m₂)/2 ＝ (定数) × u₁²

　同様に、　K’＝ (定数) × u₁’ ²　であり、　K ≧ K’　より　 u₁ ≧ u₁’




Q8.　それぞれの物体の速さが遅くなることは納得しました。　そして、計算を見ていて気が付いたのですが、全運動量０の関係、 m₁u₁ = m₂u₂　と　m₁u₁' = m₂u₂'　とを、辺辺で割れば、　u₁'/u₁＝u₂'/u₂ です。　これは速さの減少が共通であることを示しています。　物体１の速さが 0.8 倍になるのなら、物体２の速さも 0.8 倍になるのですね。


A.　なるほど、そうですね。　重心系での衝突のイメージが より明確になっています。
　私にとっても新たな知見でした。

　さて、話を運動エネルギーに戻します。　滑らかな平面上なので、重心は等速度で動いています。　そこで、重心系は慣性系です。　したがって、静止系のようにエネルギー保存則などを考えていくことができます。
　そこで注目したいのが、衝突によって失われた運動エネルギー K − K’　です。これは 静止系で見ても同じはずです。　熱などに変わった分ですからね。




Q9.　K − K’ が 静止系で見ても同じなのは、それなりに納得がいきます。　計算で示すのは大変なのでしょうか。


A.　計算の大変な部分は 実はもう終わっています。Q2 で出合った「静止系での運動エネルギーの和 ＝ 重心 G の運動エネルギー Mｖ_G²/２ ＋ 重心系での運動エネルギーの和」を用いれば、簡単に済みます。

　静止系での全運動エネルギーを K_静 とすると、衝突前について、
　　　　　　　　　　 K_静 ＝ Mｖ_G²/２ ＋ K 　 ・・・�@
　衝突後は、　　　　 K_静^’ ＝ Mｖ_G²/２ ＋ K' 　・・・�A
　�@−�A　より　　　 　　K_静 − K_静^’ ＝ K − K’

　重心が等速度なので、 Mｖ_G²/２ が一定 ですからね。　( M は全質量で、M ＝ ｍ₁＋ｍ₂)


　上の関係は、「静止系で弾性衝突なら、重心系でも弾性衝突」とも言っています。両者は慣性系なので、当然と言えば当然ですが。

Q10.　弾性衝突であれば、 K ＝ K’　ですから、 u₁ ＝ u₁’ 、 u₂ ＝ u₂’　です。
　衝突で速度の向きは変わっても、それぞれの速さが変わらないのですね。


A.　そうです。　弾性衝突は重心系ならとてもシンプルですね。

　さらには、初め片方が静止していたとすると……平面上の衝突では、最もポピュラーなケースです……跳ね飛ぶ向きについて、ある関係が成り立つのです。

　静止系での衝突の状況が 次図です。　球１が速さ v₁ でやってきて 静止している球２に弾性衝突し、その後、それぞれは速さ v₁’、 v₂’ で跳ね飛んだとします。

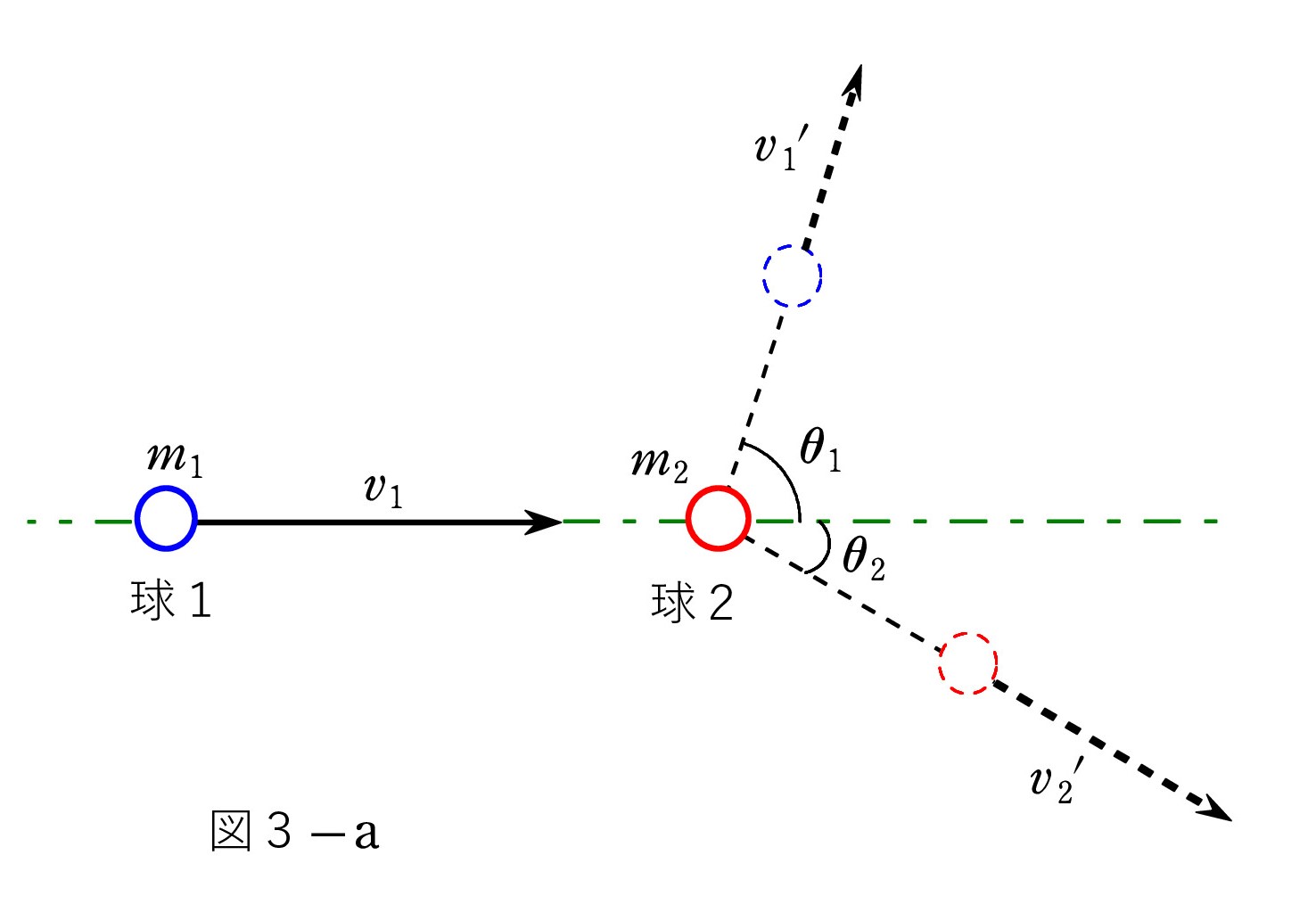
　このときの重心 G の動きも図にしてみました。 G は等速度 v_G で動き、 G に対して２つの球が逆方向に離れていくのが 分かるでしょう。

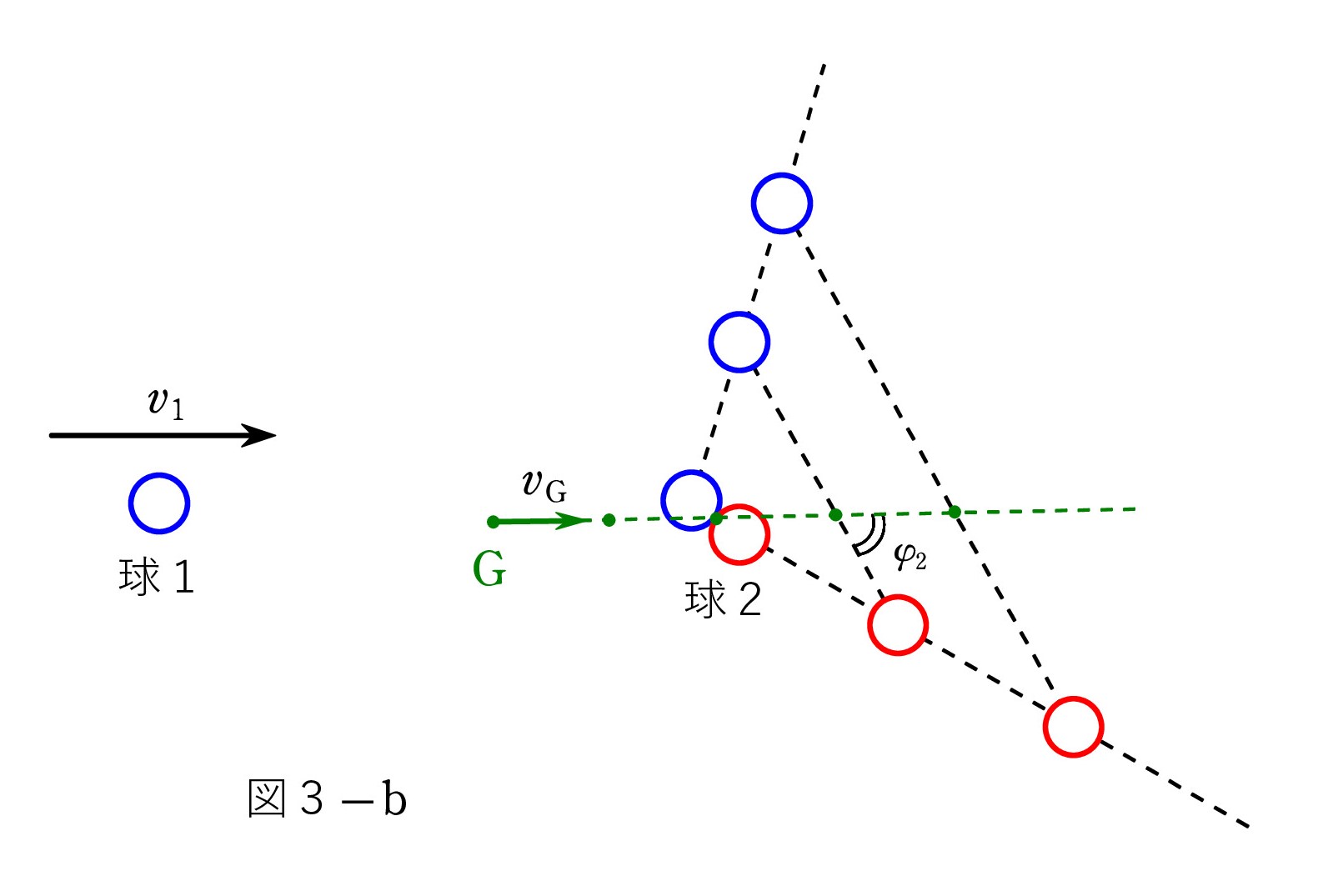
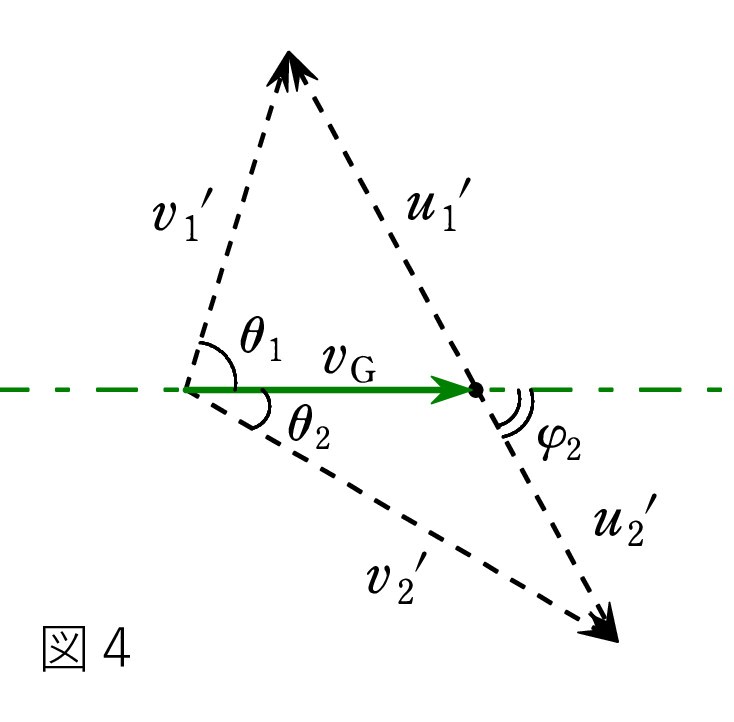　重心系での衝突後の速さを u₁’、 u₂’ とすると、図２は 図４のようになります（衝突後について)。　はじめ、球２が静止しているので、重心の速度 v_G は v₁ と同じ向きです。
　
　このとき、静止系での角度 θ₂ と重心系での角度 φ₂ の間に　φ₂ ＝2θ₂　の関係があります。

　その理由を考えてみてください。


　　　　　・・・・・・・・？・・・？・・・？・・・？・・・？・・・・・・・・





Q11.　よく分かりません・・・何かヒントを・・・


A.　ヒントは、衝突前の球２の重心系での速さ u₂ と v_G の関係がどうかということと、 u₂ と u₂’ の関係です。　球２は初め静止し、弾性衝突です。


　　　　　・・・・・・・・？・・・？・・・？・・・？・・・？・・・・・・・・





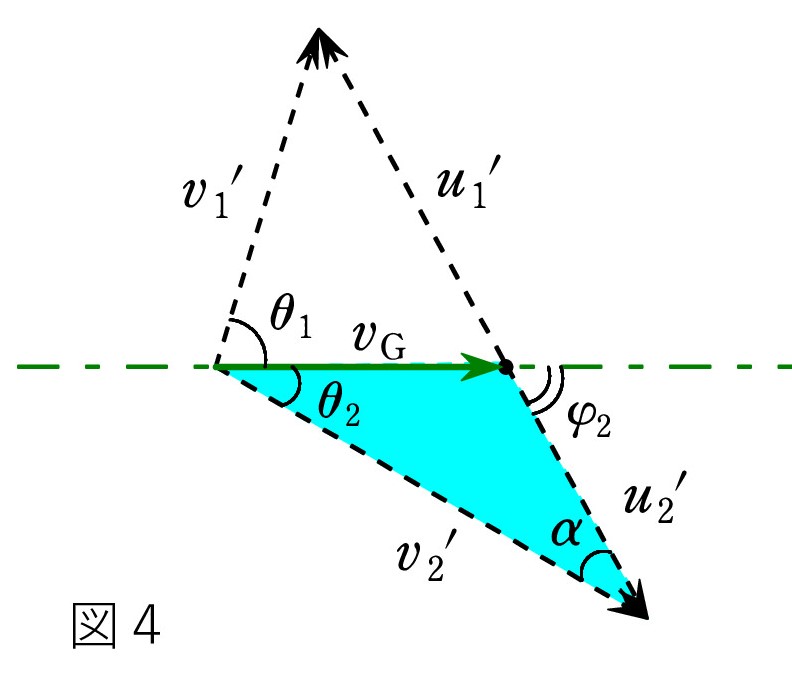Q12.　分かりました。　球２は静止していたので、 重心 G から見た球２の速度は重心の速度を逆向きにしたものです。 だから、 u₂ ＝ v_G です。
　そして、弾性衝突だから、 u₂’ ＝ u₂ です。
ということは　 u₂’ ＝ v_G ですね。　なるほど、空色の三角形は二等辺三角形で、α＝ θ₂ なんだ。
　 φ₂ ＝ θ₂ ＋α　だから、　 φ₂ ＝ θ₂ ＋ θ₂ ＝2 θ₂
というわけですね。

A.　それで OK です。

　先ほどはヒントを出しましたが、入試ではそうはいきません。　問題が解けないとき、あるいは解く方針が定まらないときは、逆順で考えるのも有力な方法です。
　今の例なら、 φ₂ ＝ θ₂ ＋α　という幾何学に目を向ければ、α＝ θ₂ を示せればいい　→　空色の三角形が二等辺であればそうなる　→　 u₂' ＝ v_G　を示せばいい ・・・ という思考回路です。　幾何学の証明でよく用いられていることは 知っているでしょう。
　



Q13.　重心系では、弾性衝突したそれぞれの球が速さを変えないとなると、衝突後の運動方向だけが未知です。　それを決めるのは何なのか が気になっていました。
　２つの球は正反対の向きに飛ぶので、φ₂ が決められればいい。　そして、φ₂ を決めるのは θ₂ だというわけですね。
　すると、問題は θ₂ を決めるのは 何なのか というところまで煮詰まりました。　何なのでしょうか？


A.　斜めに飛ぶ原因は、２つの球の中心がずれているからです。
　滑らかな２球の衝突であれば、 θ₂ は衝突時の状況から決まります。

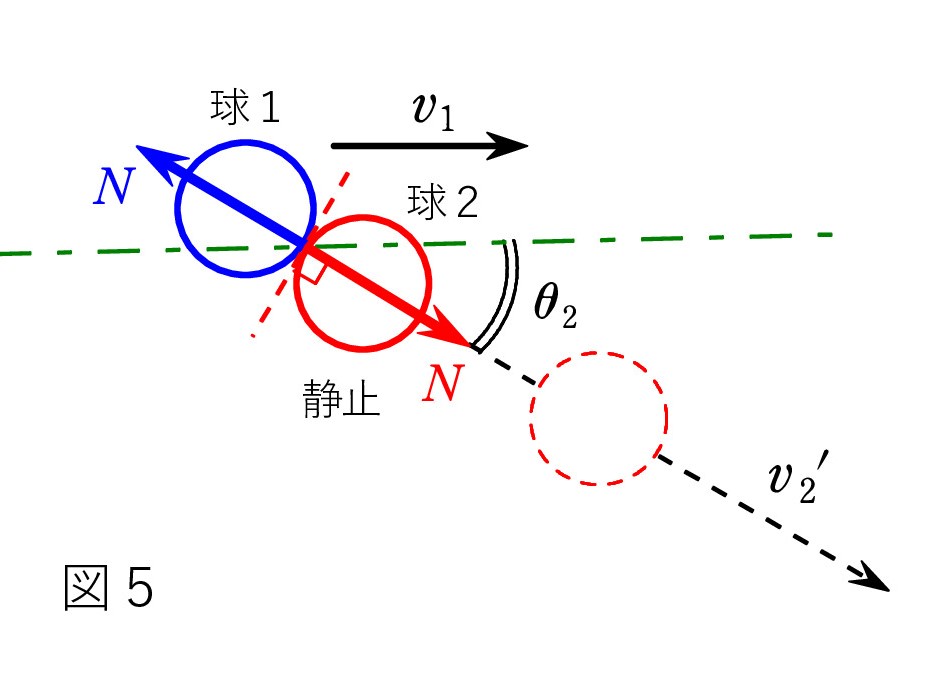　右図のように垂直抗力 N（赤矢印）が働き、静止していた球２は力の向きに動き出します。　これは初速度が 0 だから言えることです。
　初速度をもつ球１の衝突後の速度は力の向き（青矢印 N ）とは一致しません。「 力積 ＝ 運動量の変化 」に基づいて、ベクトルの関係になります。
　落体の運動でも初速がなければ、重力の向きに動き出し、自由落下となりますが、初速度があれば、斜め方向の放物運動ですね。


　余談ですが、この図はビリヤードでは最も基本となることです。
　止まっているボール(球２)をある方向に動かしたいのですが、手玉(てだま)と呼ばれる球１を長い棒で突いて球２に当てます。　球２は的玉(まとだま)と呼ばれます。
　θ₂ の方向に動かしたいなら、図のような位置に手玉の球１を持ってくればよいのです。　言い換えれば、２つの球の中心を結ぶ方向です。　それをイメージして、長い棒(キュー) で手玉を突きます。




Q14.　ビリヤードなら、一度やったことがあります。ポケットビリヤードというゲームで、台の縁に空けられた穴に的玉(球２)を落としたいのですが、その時、教わりました。


A.　ついでのことに、ビリヤードではボールの質量が等しいので、 θ₁ ＋ θ₂ ＝90° となります。衝突後の２つは直角方向に動くということですね。
　これもゲームを楽しむ上で必要な知識となっています。　衝突後の手玉が穴に落ちると失点につながるので。　穴はポケットと呼ばれ、台の周囲６箇所にあるので、油断できません（長方形の台の角４箇所と、長い辺の中央２箇所)。

　もちろん、正面衝突ではないとします。　正面衝突なら、「等質量の弾性衝突( e ＝１)は 速度の交換」ですね。　今の場合は、手球１が止まり、的球２が速さ v₁ で動き出します。 ビリヤードでも、手玉と的球の中心を結ぶ直線上にポケットがあれば、これを利用します。
　手玉がポケットに入る心配がないケースですが、正面衝突は意外に難しく、初心のうちは的球がポケットをそれることがしばしばです。

　大分 脱線しました。 話を物理に戻します。
　平面上での弾性衝突は入試問題でも扱われることがありますが、誘導に乗って計算を進めれば済みます。　念のために確認しておきますが、そのとき用いるべき法則は ？



Q15.　エネルギー保存則と運動量保存則です。　 運動量保存はベクトルとしての保存則 なので、ｘ、ｙ各方向について成り立ちますから、都合３つの式ができるということですね。


A.　その通りです。　エネルギー保存則は、弾性衝突では運動エネルギーの総和の保存ですね。
　弾性衝突でない場合にも、運動量保存則は成り立つことに注意してください。 しかも、ベクトルとしてです。　計算では、直角をなす２方向に分解して扱いますが、ベクトルの図で対処すると早いことがあります。

　さて、片方が静止している ２球の弾性衝突で、質量が同じ場合、あとは誘導に従って計算していけば、やがて、 θ₁ ＋ θ₂ ＝ 90°　にたどり着けるはずです。
　ただ、今まで話してきたことから、計算しなくても導けるのです。問題にしてみます。

「 弾性衝突で、m₁ ＝ m₂　の場合、 初め片方が静止していれば、 θ₁ ＋ θ₂ ＝ 90° となることを、図を利用して示せ。」
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　解答（※+※）は最後に

Q16.　「運動量保存則はベクトルの図にすると、早く解けることがある」という実例には「エッセンス」でも出合っています。　図３の衝突問題では、次の 図６a あるいは ベクトルを並べ替えた図６b になりますが、役に立たないケースということのようですね。

　　　　　

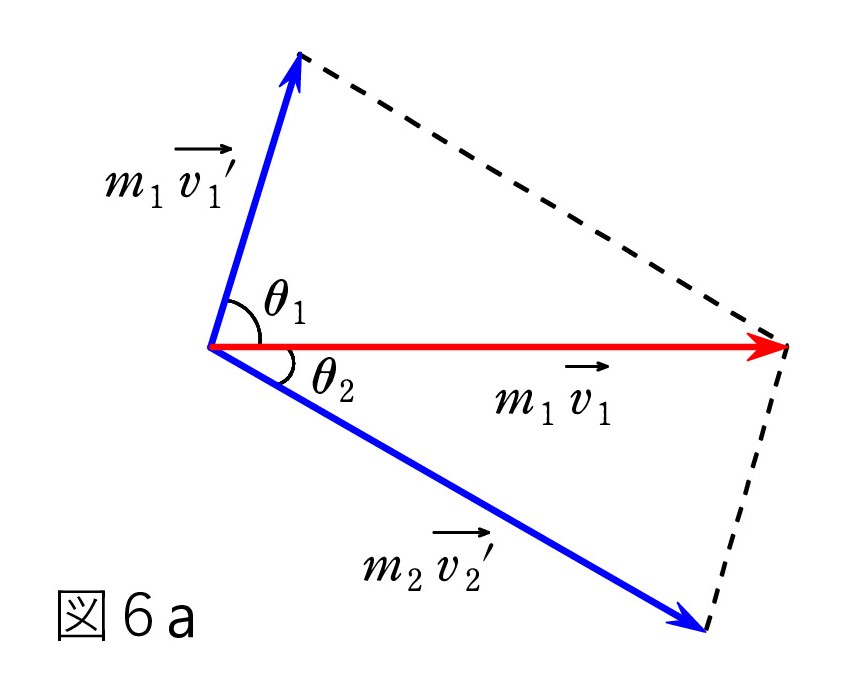
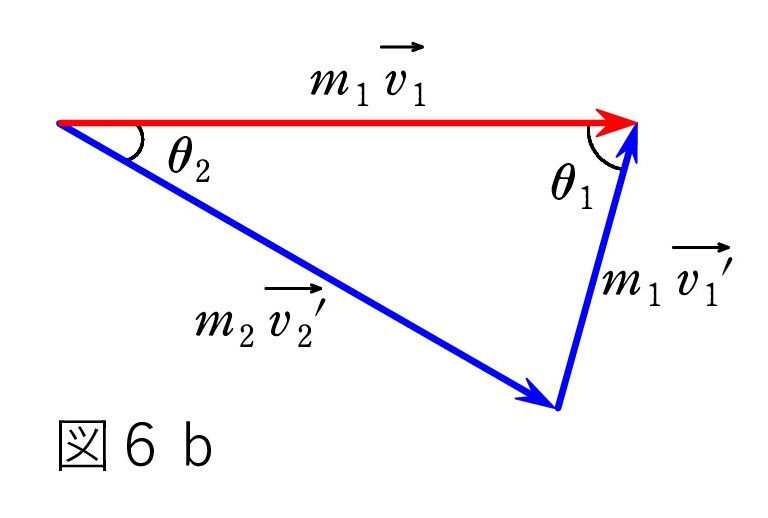
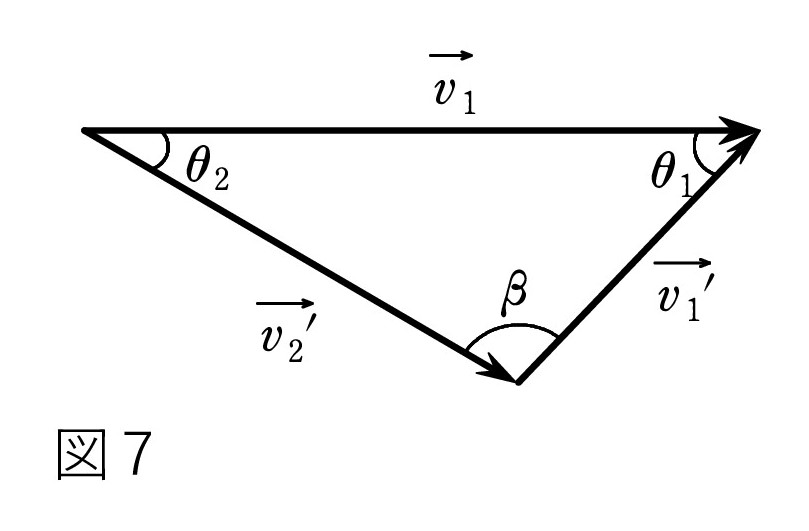
A.　実は、今扱っている「ビリヤード問題」なら 大いに役立つのです！
　m₁ ＝ m₂ の場合には、図６b は図７のように速度の関係になるでしょ。　ただし、このままでは大したことはありません。

もう一つの条件を思い起こすと・・・

　　　　　・・・・？・・・？・・・？・・・・

　



Q17.　弾性衝突で、エネルギー保存則ですね。

　　　　 mv₁²/2 ＝ mv'₁²/2 ＋ mv'₂²/2　　　 ∴　v₁² ＝ v'₁² ＋ v'₂² ・・・�@

　図７と両立するということは・・・図７が直角三角形ならピタゴラスの定理です！
　β が直角なら、 θ₁ ＋ θ₂ は 90°ですね。　なるほど・・・
　・・・ でも、直角三角形でなければならないと言えますか ？


A.　確かに、「直角三角形なら OK 」では十分条件に過ぎません。
　　 ヒントは 三角形に対する「あの定理」です。

　　　　　・・・・？・・・？・・・？・・・・




Q18.　３つの角が現れているので、正弦定理かとまず思いました。
　でも、�@を活かしたいので、余弦定理ですね。

　図７で、角度 β に対して、　　v₁² ＝ v'₁² ＋ v'₂² −２v'₁ v'₂ cos β

　�@ を用いると、　　 ０＝−２v'₁ v'₂ cos β　つまり　 cos β＝０　　∴　β ＝ 90°

　したがって、 θ₁ ＋ θ₂ は 90° ということですね。


A.　それで OK です。　ベクトル図のお陰で、計算と言えるほどのものでなくなっているのが分かるでしょう。

　入試では、ｘ,ｙ方向に分けて、運動量保存則を扱い、しっかり計算力が問われると思います。　大学の先生には 計算によって導くものという固定観念があることも一因です。　私自身も 今回の質問に出合うまではそう思っていました。

Q19.　ところで、斜めに飛び散る場合、反発係数（はね返り係数）e は役に立たないのでしょうか？


A.　反発係数は 基本的には 直線上の正面衝突に対してのものです。

　ただ、工夫すれば、用いることができます。
直線上とは衝突の際の垂直抗力の方向でもあるのです。
　たとえば、上の図５なら垂直抗力が働く方向、つまり、 θ₂ 方向の速度成分に対して適用できます。
球２が初め静止している必要はなく、衝突時における２つの球の中心を結ぶ直線方向です。　その方向では正面衝突と同じ力学になります。
　一方、滑らかな２球が接触している赤点線方向では力が働かないので、各球の速度成分は不変です。

　弾性衝突でない場合、エネルギー保存則が使えないので、運動量保存則と反発係数 e の式で対処することになります。　上記の方向（衝突時の２つの球の中心を結ぶ直線方向）についてです。　直線上での正面衝突のときと同様になります。
　ただ、斜め衝突での反発係数は お話だけでいいでしょう。




Q20.　反発係数で思い出しましたが、直線上の正面衝突では、球と直方体の衝突でもよかったのに、斜め衝突では球どうしの衝突になっています。他の本でもそうです。
何か理由があるのでしょうか。


A.　衝突によって回転（自転）が生じる可能性があります。それを避けるために「滑らかな２つの球」にしています。球でも摩擦があれば、回転につながるので。　「２つの小球」として、回転が無視できることを表す場合もあります。
　でも、出題者だけが気にすればいいことです。




Q21.　反発係数 e の式は なぜ成り立つのでしょうか？
　e＝−(v'₁−v'₂)/(v₁−v₂) です。　教科書では 単に「成り立つ」とあったり、定義式のように書いてあったり、曖昧なこと この上もありません。
　式を言葉に直すと、「衝突前後の相対速度の比が一定」となり、 何か意味付けができそうなのですが、もう一つ、スッキリしません。


A.　実験法則、分かりやすく言えば 経験則と思ってください。
　理論的には、簡単化したモデルに基づいて説明がなされています。ある程度の理由付けはできるものの、基本的な位置づけとしては 実験法則です。

Q22.　重心系に戻りたいと思います。　衝突以外で重心系が役立つことはありますか。　そして、重心系を用いる場合、重心の運動の知識が必要です。「エッセンス」では、運動量保存則が成り立つときは、つまり、物体系に外力が働かなければ、重心は等速度で動く となっています（（上）ｐ66 (新版 p 67) ）。　それ以外に、重心の運動について 何か知られていることがありますか ？


A.　物体系の全質量を M 、重心 G の加速度を a_G とし、物体系に働く外力を F とします（ a_G と　F は ベクトル）。　物体系を構成する一つ一つの物体に働く外力の総和（ベクトル和）が F です。
　すると、　M a_G ＝ F　が成り立つことが証明されています。重心の運動方程式ですね。
　重心 G は、運動方程式に従って 外力によって運動し、物体間で働く内力には影響されない のです。

　 　F ＝ ０ なら　 a_G ＝ ０ であり、重心 G は等速度（等速直線運動）で動くことになります。静止も含みます。　 これが「エッセンス」でふれたケースです。
　上で登場した、ばねで結ばれた A と B の運動がそうでした。　他の例としては、２つの物体が滑らかな水平面上で衝突するとき、正面衝突はもちろんのこと、斜め方向の２次元衝突で物体が別々の方向に飛び散っても、重心は衝突の前後を通して等速度で動いています。

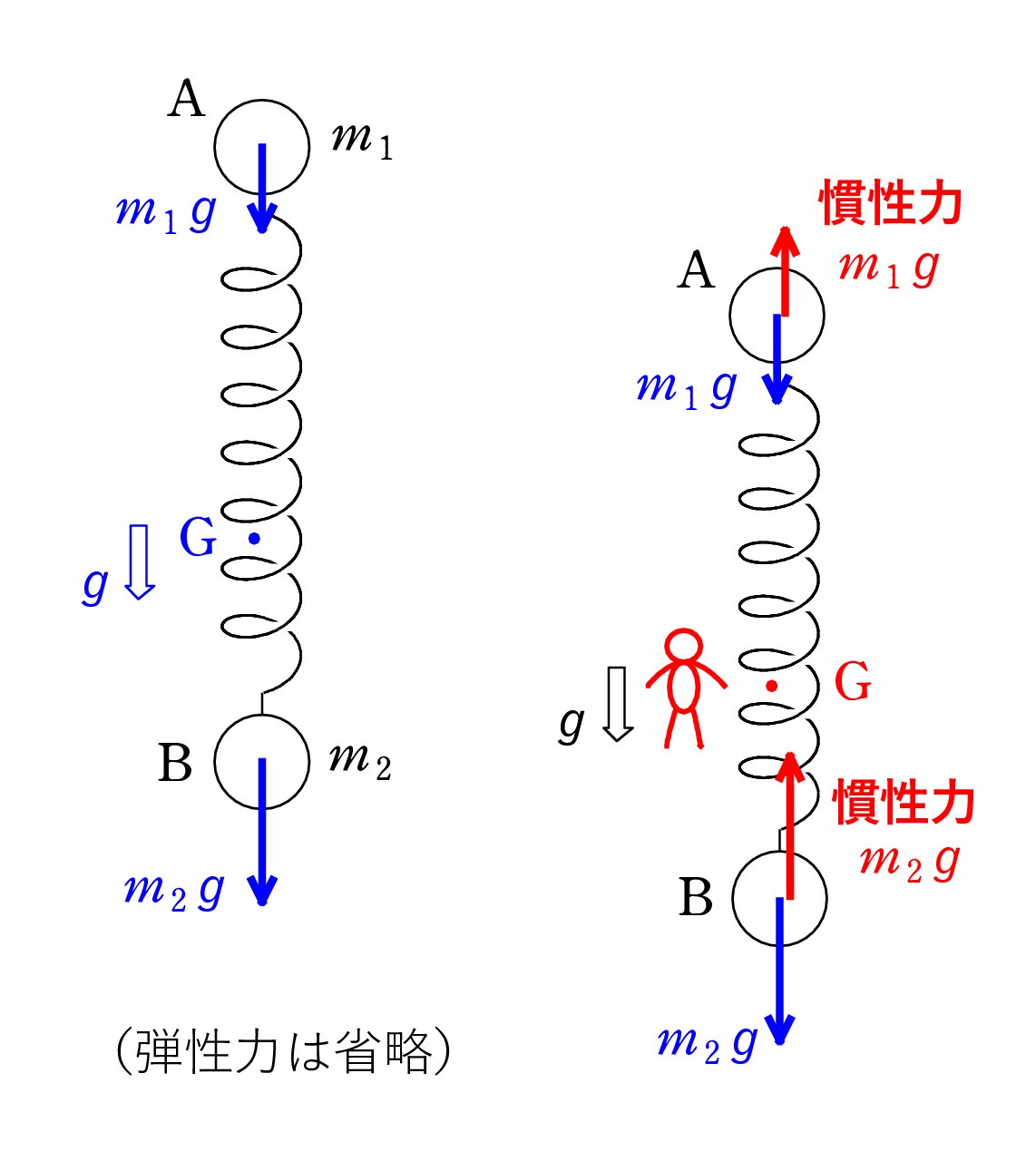　もし、A を持って B をばねでぶら下げ、A を放すと・・・A と B それぞれは複雑な運動をしますが、　重心 G は重力加速度 ｇ で 自由落下します。
　上式で、 F ＝ M g であり、 a_G ＝ g　だからですね。

　そして、重心系に移ると、全運動量０だけでなく、驚くべき事態になっているのです。
　慣性力が A と B に対して上向きに働き、重力を完全に打ち消しています。　水平面上でのばねによる振動と同じことになっているのです。自然長の位置が振動中心になる単振動です。

　まさに、 重心系 の 面目躍如 ！


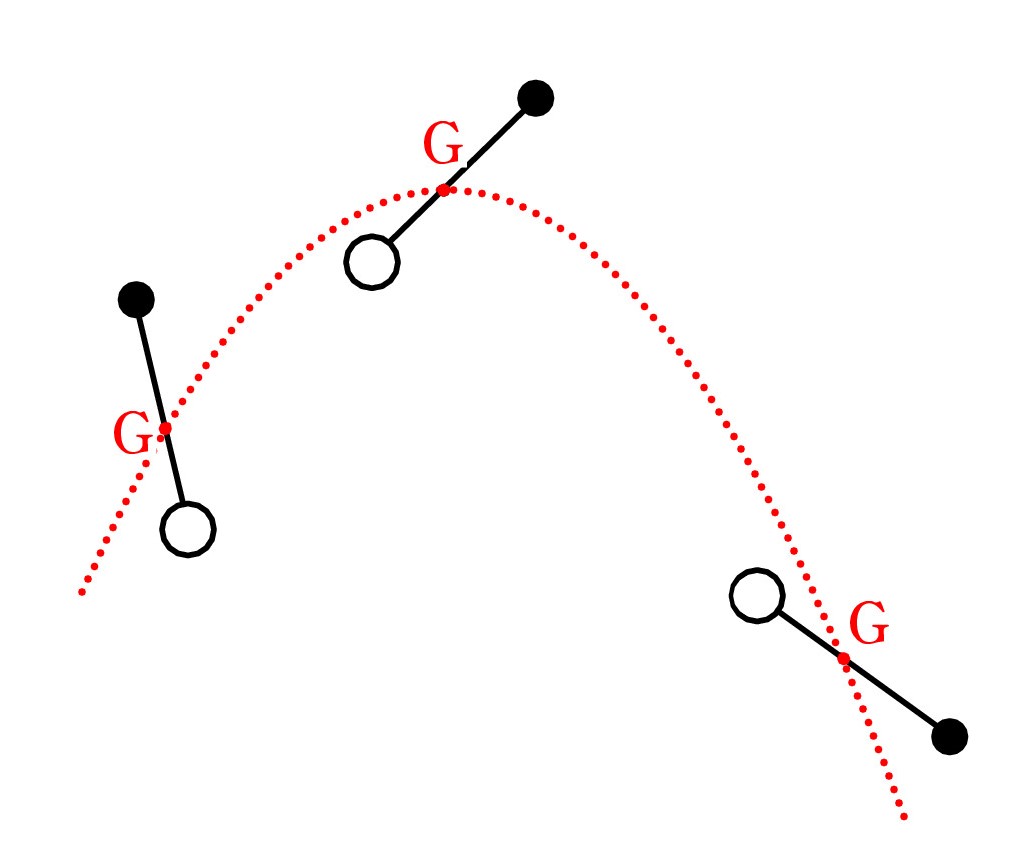
　２つの物体を棒で結んで、適当に放り投げると・・・重心 G は放物運動 ですね。そして、重心系では、重力がないのと同じで、２つの物体は というか、棒は等速回転に入ります。　G が中心となる角速度 ω が一定の回転です（ ω＝０ も含む )。


　以上は、高校の範囲を超えていますが、入試では誘導しながら出題されることがあり、しかも、このところ増加傾向にあるので、意識しておいた方がよいでしょう。







Q23.　重心の運動方程式　Ｍ a_G ＝ Ｆ の 証明はできませんか ？


A.　ベクトルでの証明は大学の数学が必要なので、ここでは２物体が互いに力を及ぼし合いながら、直線上を運動するケースで導出してみます。本質は十分理解できます。
速度 ｖ の時間微分 dv/dt が 加速度 a になることは知っているものとします。

　物体１、２が受ける外力をＦ₁ 、Ｆ₂ とすると、それぞれの運動方程式は、
　　　ｍ₁ a₁ ＝ F₁ ＋ f₁₂　・・・�@　　　　　m₂ a₂ ＝ F₂ ＋ f₂₁　・・・�A
　ｆ は 互いに及ぼし合う力（内力）で、ｆ₁₂ は 物体１が２から受ける力、ｆ₂₁ は ２が１から受ける力です。
　そして、作用・反作用の法則 により　　　f₂₁ ＝ −f₁₂
　�@ ＋ �A とすると、内力は消え去り、　　m₁ a₁ ＋ m₂ a₂ ＝ Ｆ₁ ＋ Ｆ₂　・・・�B

　一方、重心の速度 ｖ_G ＝（m₁v₁＋m₂v₂）/(m₁＋m₂）を時間 ｔ で微分すれば、左辺は加速度 a_G になり、右辺では a₁ 、a₂ が現れて、
　　　　　　　dｖ_G/dt ＝（m₁ dv₁/dt＋m₂ dv₂/dt）/(m₁＋m₂）
　　　　　　　　 　　a_G ＝（m₁ a₁＋m₂ a₂）/(m₁＋m₂)　　　　　　・・・�C

　�B と �C より　　(m₁＋m₂）a_G ＝ F₁ ＋ F₂
　こうして　　Ｍ a_G ＝ Ｆ　が得られます。






＃＃＃＃　Dialogue はここまで　＃＃＃＃

＃＃＃　Dialogue （対話）：　Q1 〜 Q18　＃＃＃＃＃

　　―――――　遠心力と慣性力　・　単振り子　・　万有引力　―――――



Q1.　『Q＆A エッセンス』では、円運動に対しては、向心加速度を用いた運動方程式ではなく、遠心力による力のつり合いが勧められています。遠心力の重要性は分かりましたが、前から気になっていることがあります。
　それは、鉛直面内での円運動のように、等速でない場合にも 遠心力 ｍｖ²/ｒ が用いられていることです。　この式の証明は教科書にありますが、等速円運動に対してのものです。　飛躍があるのではないでしょうか。　　　　　　（ ｍ：質量　　ｖ：速さ　　ｒ：円の半径 ）


A.　確かに気になりますね。　導出の過程は、まず、加速度に関する次の資料を見て下さい（参考書「物理教室」からの引用)。　半径方向と接線方向に分解して考えています。　等速円運動での証明を利用しているのがミソです。

• 「物理教室」からの引用

　結局、等速でない円運動でも半径方向に注目すると、加速度 a は円の中心を向き、
a ＝ ｖ²/ｒ です。
　そこで、この加速度で動く観測者を考えると、慣性力 ｍa ＝ ｍｖ²/ｒ が外向きに働くことになります。それが遠心力です。「 遠心力を考えれば、半径方向は力のつり合い」となります。




Q2.　接線方向はどうなっているのですか。


A.　接線方向では慣性力を用意していないので、加速度 a’ での加速度運動です。
　 a’ には一般的な表現がなく、慣性力を用意できないと言った方がよいかもしれません。

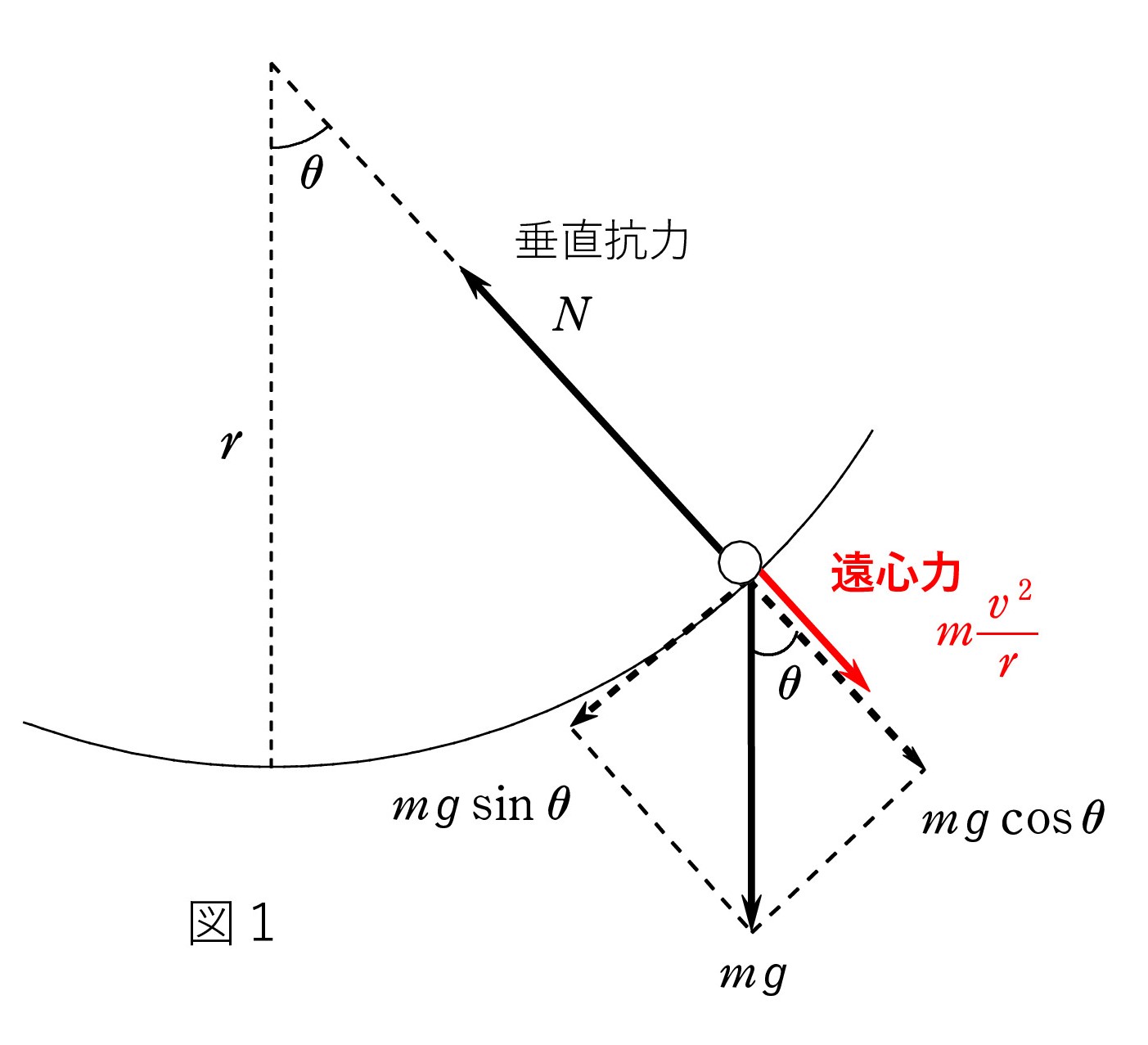
　たとえば、図１のように滑らかな円筒面上を滑る小球なら、接線方向について、
　運動方程式　ｍa’＝ｍｇsinθ　から　a’＝ｇsinθ　と決まります。　ただし、θ と共に変わり、等加速度ではないので、それ以上には話が進みません。
　 a’ の向きは ｍｇsinθ の向きで、上がるときは減速、降りるときは加速です。

　一方、半径方向では遠心力が働き、力のつり合いは　N ＝ ｍｇcosθ ＋ ｍｖ²/ｒ です。
　図は、小球が速さｖで上がるときでも 降りるときでも どちらでもいいです。




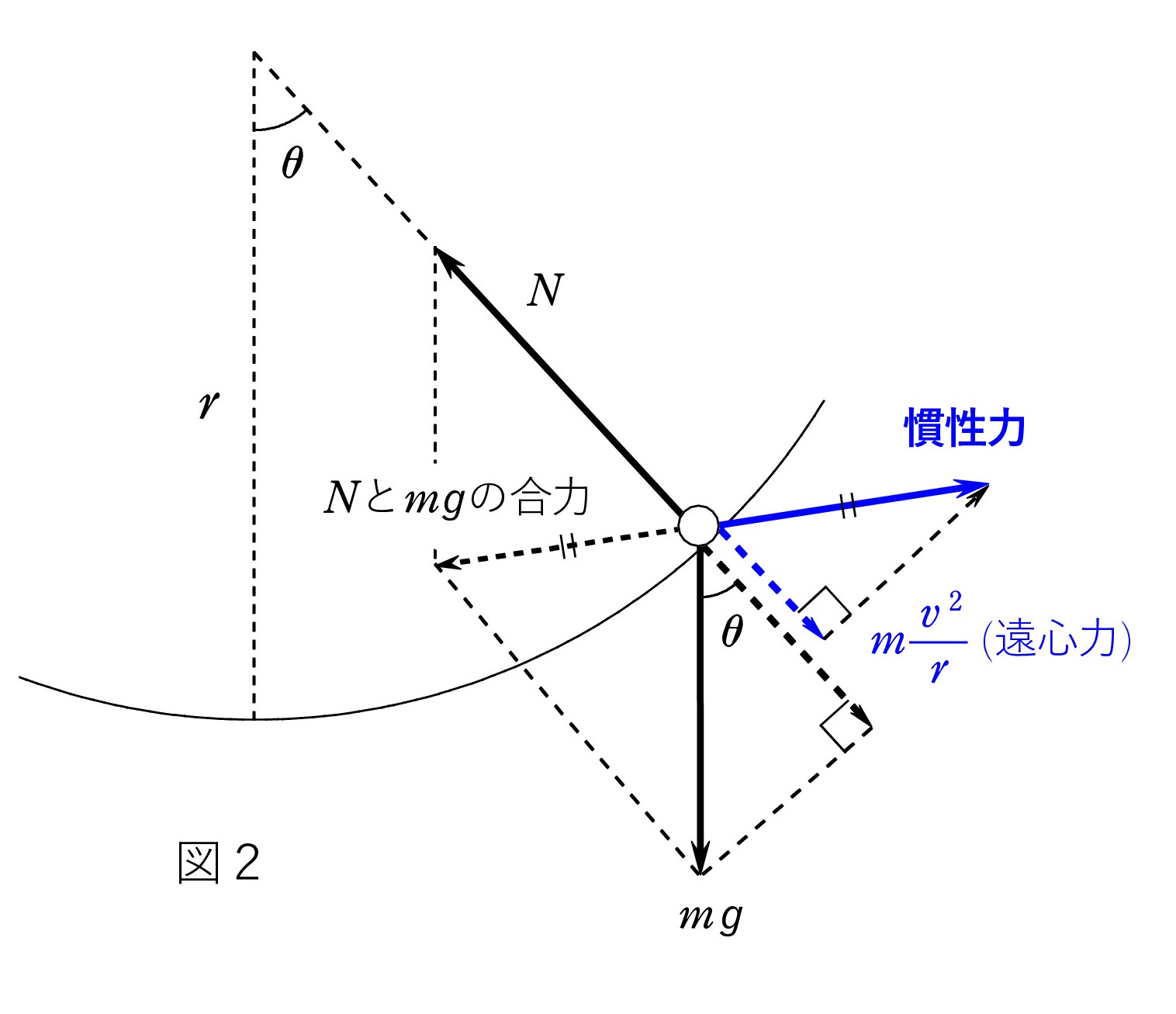Q3.　学校では、図２のように、重力と垂直抗力（の合力）につり合う力として、慣性力を青矢印のように描きます。　その半径方向の成分が遠心力です。
　慣性力とはこのように「力のつり合い」を成り立たせるものではないのでしょうか。



A.　そのように説明している教科書もあります。
　確かに、小球とまったく同じ円運動をしている観測者にとっては、小球はいつも静止して見え、完全な力のつり合いになりますね。　その点は分かりやすいのですが、賛成できません。
　本末が転倒しているのです。まず、観測者の加速度を決め、それに応じて慣性力を考えるというのが、本来の手順です。　観測者の加速度、言いかえれば、小球の加速度を求めずに、「結果」である力のつり合いを利用して慣性力を描いているに過ぎません。　Ｎが未知なので、慣性力も未知です。
　慣性力をあらかじめ押さえていないので、接線方向も力のつり合いですが、新たに何かが分かるわけではありません。




Q4.　なるほど。　結局は接線方向には目を向けず、半径方向について、遠心力による力のつり合いにより　N＝ｍｇｃｏｓθ＋ｍｖ²/ｒ としています。　慣性力(青矢印)を描いた手間がかかっただけのような気がしてきました。
　青矢印を分解し、青点線のように半径方向分を取り出して、遠心力 ｍｖ²/ｒ に置き換えるというのも 回り道の感じがします。


A.　はじめから半径方向だけに注目しているのが図１です（図２を簡略化したわけではありません)。　想定している観測者は半径方向・円の中心向きに加速度 ｖ²/ｒ で動いている人です。　速さｖで等速円運動している人と言ってもいいでしょう。

　半径方向と接線方向は独立で、分解して扱うという姿勢が大切 です。　繰り返しになりますが、半径方向は遠心力による力のつり合い、接線方向は加速度運動 という認識の方が優ると思います。　接線方向の速度、つまり、速さが変わっていくのは常識でしょう。

Q5.　接線方向の運動というのがもう一つピンときません。　円弧の沿っての運動という意味だと思いますが、それ自体が問題になることもあるのですか。　もちろん、力学的エネルギー保存則で解ける場合は除いての話です。
　

A.　身近なところにありますよ。　「円運動」ではなく、「単振動」で習うので、気がついていないのでは ？・・・

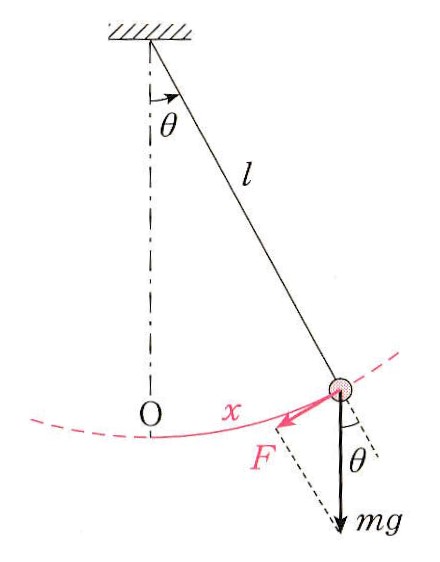　単振り子です。　長さｌの糸に付けられたおもりは円弧に沿って運動し、接線方向の運動を決めるのは、重力の接線成分です。これが復元力Ｆとして働き、　Ｆ＝ｍｇsinθ　です。
　θ が微小なら sinθ ≒ θ と近似でき、最下点Ｏからの円弧の長さをｘとすると、 θ＝ｘ/ｌ から 復元力は　Ｆ＝Kｘ　の形になり、単振動と分かります（ K＝ｍｇ/ｌ )。　したがって、周期は
Ｔ ＝ 2π √(ｍ/K )＝ 2π √(ｌ/ｇ)　ですね。　　（ π：パイ、円周率 ）

　正確には、ｘは円弧に沿った曲線座標軸での座標で、Ｏが原点です。符号を含めて向きを表せば、Ｆ＝−Ｋｘ です。


　入試では、円弧全体に渡る問題も出されています。

鉛直面内の円軌道を、加減速が可能なジェットコースターが 接線方向に一定の加速度 β で回る ―― という問題です。　どう対処したらいいでしょう ？



　　　　・・・・・・・・？・・・？・・・？・・・？・・・？・・・・・・・・



　半径方向は遠心力によるつり合いで、接線方向は運動方程式ですね。　接線方向に加速する力をｆとすると、　ｍ β ＝ ｆ − ｍｇsinθ　となり、　ｆ ＝ ｍ（ β ＋ ｇsinθ ） のように、ｆ が θ の関数として表せます。
　そして、運動に対しては、等加速度直線運動の公式の応用です。　加速度 β を用いて、公式のｘを「円弧の長さ」に置き換えればすみます。速度ｖはもちろん接線方向の速度です。　直線運動の公式が曲線運動にも応用できるというのがポイントです。　では、

　　初速０のとき、半径ｒの円軌道を一周する時間ｔは ？　一周後の速さｖは ？


　　　　・・・・・・・・？・・・？・・・？・・・？・・・？・・・・・・・・



　２πｒ＝１/２・βｔ²　から　ｔ ＝ ２√(πｒ/β)　ですね。
　また、ｖ ＝ βｔ ＝２√(πｒβ) 　です。　　ｖ² − ０²＝２β・２πｒ　として求めてもいいでしょう。　いきなりｖが問われれば、この式でいきます。

　少し悪ノリかもしれませんが、次の問いはどうでしょう。

　　　　　　　　一周する間に外力ｆがした仕事 Ｗ はいくらですか ？


　　　　・・・・・・・・？・・・？・・・？・・・？・・・？・・・・・・・・



　エネルギー保存則から、１回転で物体が獲得した運動エネルギーに等しいはずで、
　　　　　　　　　Ｗ ＝ 1/2・ｍｖ²＝２πｍｒβ
　ていねいに、定理　非保存力の仕事＝力学的エネルギーの変化 を用いて、この場合は、
外力ｆの仕事 Ｗ ＝ 運動エネルギーの変化　であり、　Ｗ ＝ 1/2・ｍｖ²−０　として求めてもいいでしょう。

　あるいは、上で調べた　ｆ＝ ｍ（ β ＋ ｇsinθ ）を利用することもできます。
　ｆ が一定なら、ｆ×２πｒ　になるはずですが、sinθ の項が目に入ります。　θ＝０〜π と θ＝π〜2π で 最高点(θ＝π)を境に対称的ながら、符号が反転して打ち消すと気付けば、
　　　　　　　　　Ｗ ＝ｍβ ×２πｒ＝２πｍβｒ
　このように力が一定でない場合にも、仕事が直接計算できることがあるのは、意識しておくとよいでしょう。




Q6.　要領がつかめたと思います。　最下点から出発するとして、最高点までの外力ｆの仕事 Ｗ’ も出せそうです。
　最高点での速さを u とすると、　u²−０²＝２β・πr　であり、　直径 2r 分 高く上がることを考えて、　Ｗ’ ＝ 1/2・ｍu² ＋ ｍｇ・2r ＝ ｍｒ(π β ＋ 2g)　です。

　さらには、β＜０ のケースも「あり」ですね。　初速 v₀ を与えると、しばらくして止まり、逆回転が始まります。　 止まるまでに進む距離ｓは、 ０²− v₀² ＝ 2β s で決まります。　もちろん、ｓは円弧の長さです。

　さて、単振り子の話に戻りたいと思います。　何かと興味をひかれる存在で、いくつか疑問に思っていることがあります。
　まず、周期の公式 Ｔ＝ 2π √(ｌ/ｇ)　は、振幅 A が小さいという条件が必要でした。
　θ が微小角のときの近似式 sinθ ≒ θ を用いたいので、そうなっているのですね。



A.　その通りです。
　大きいとか、小さいとかというのは 何に比べてかと考えるのも大切 です。　たとえば、「0.1ｍｍ は小さい」はもっともらしく聞こえますが、１μｍ(１ミクロン) からすれば、100倍もの大きな値です。　無意識のうちに、日常出会う物体の大きさと比較して、「0.1ｍｍ は小さい」と判断しているのです。
　単振り子の場合は、振幅 A が糸の長さｌに比べて小さいことが 単振動の条件ですね。

　そうであれば、周期Ｔは振幅に依らず一定 であることも大切です。振り子の「等時性」と呼ばれています。　一般に、単振動と決まれば、周期は振幅に依りません。
　おもりの質量 ｍ に依らない のも面白いですね。　ばね振り子は Ｔ＝ 2π √(ｍ/ｋ) と、ｍ に依っています。　「重いものほど動きが悪い」という「常識」を裏切っているのが面白いのです。　この「常識」は「力が同じなら」という前提でのものですが（運動方程式 ｍa ＝ Ｆ に基づいて）、いまは復元力Ｆが ｍｇsinθ と、ｍ と共に大きくなっているのです。

　では、ここで問題です。定性的な思考力を要する難問ですが、入試でも時に見かけます。ヒントも付けておきます。

　　　　　振幅が小さくない場合は単振動ではないが、周期運動である。
　　　　　その周期 Ｔ‘ は Ｔ＝ 2π √(ｌ/ｇ) より長いか、それとも短いか？

　　　　　　ヒント
　　　　　　　　　　　　　　　　　　　　　　　　　　　　解答（※X1※）は最後に

Q7.　 Ｔ＝ 2π √(ｌ/ｇ)　は、微小角という制限が必要ですから、本当に微々たる振動にしか使えないのでしょうね。


A.　そう思ってしまいそうですね。　ところが、実際にはかなり大きく揺れる振り子でも大丈夫です。　Ｔ’ の計算には大学の数学が必要ですが、振幅Ａに対応する最大の角を θ_max とすると、10° や 20° なら T でほとんど正確で、 θ_max ＝ 45°　でも　Ｔ’/Ｔ ＝ 1.04　ですから、公式の実用性は驚くべきものです。
　念のためですが、 sinθ ≒ θ のときの θ は ラジアン〔rad〕です。

　なお、先ほどの問題の解答を見て気づいた人もいるかと思いますが、単振動と近似できる範囲でも、厳密には Ｔ’ ＞ Ｔ となっています。　振幅が大きい場合ということで話が進んでいますが、その内容は振幅が小さくても成り立つはずです。


　ついでながら、

　単振り子の実験で周期を測るとき、注意すべきことがあります。 何かは いいですか？






Q8.　 学校で実験をやりました。　周期が短いので、１回で測ると誤差が大きくなります。　何回か分をまとめて測ることだと思います。　10回分とか・・・


A.　そうです。　一般に 小さな量の測定では、たくさん集めて測るというのが鉄則 です。
　たとえば、紙１枚の厚さが知りたければ、100枚の厚さを測るとよいでしょうし、米粒１個の重さなら、100個とか、200個集めて測るといいですね。　おっと、「重さ」ではなく「質量」と言わないと叱られるかな。
　紙１枚や米粒１個が測れたとしても、厚みや質量にはバラツキがあります。　100枚や100個だと、自動的に平均値が得られているのも意識したいことです。

　振り子の周期の測定でもう一つ注意したいのは、振動の区切りとして、振動中心を通るときと 振動の端に来たときの どちらを選んだらいいか ということです。　回数のカウントで必要です。



　　　　・・・・・・・・？・・・？・・・？・・・？・・・？・・・・・・・・



　振動中心の位置は定めにくく、端は定めやすいので、端を選んでしまいそうです。　位置の誤差についてはその通りなのですが、今大切なのは時間の誤差です。
　振動中心は最大の速さで通過するので時間の誤差が小さいのです。　一方、端での速さは０なので、ストップウォッチを押すタイミングに迷ってしまい、誤差が大きくなってしまいます。　したがって、最下点の振動中心を通るときで回数をカウントし、ウォッチを押すべきです。


　以上の二点は意識してください。　あと、糸にも質量があるので、それを無視できるように、おもりの質量を大きくしたいのですが、すると、おもり(球)の大きさが必然的に大きくなります。　そこで、公式の l は　ｌ＝（糸の長さ）＋（おもりの半径）とします。おもりの重心が半径ｌの円弧を描くからです。

　さて、ｌをいろいろに変えて実験し、周期Ｔを測定したとき、Ｔ＝ 2π √(ｌ/ｇ ) の関係が成り立っているかどうかを、グラフを描いて調べたいのですが、

　　　横軸をｌ、縦軸をＴとして描くのは素直ですが、もっとよい描き方があります。
　　　どのような描き方でしょうか ？

　　　　　　　　　　　　　　　　　　　　　　　　　　　　解答（※X2※）は最後に

Q9.　単振り子の周期の公式の導出ですが、 円弧に沿っての曲線座標軸ではなく、ふつうの座標軸（水平ｘ軸・鉛直ｙ軸）でも公式を導けるのでしょうか。
　学校の先生の話では、θ が小さいので、円弧のｘは 水平ｘに置き換えてよいからということでした。　しかし、復元力 Ｆ＝ｍｇsinθ は 重力に基づいています。　鉛直方向の重力が いつの間にか水平方向の運動に関わる というのは、トリッキーな気がします。
　水平ｘ軸、鉛直ｙ軸できちんと議論できないのでしょうか。


A.　できます・・・が、余り勧めません。　以下は参考程度に。

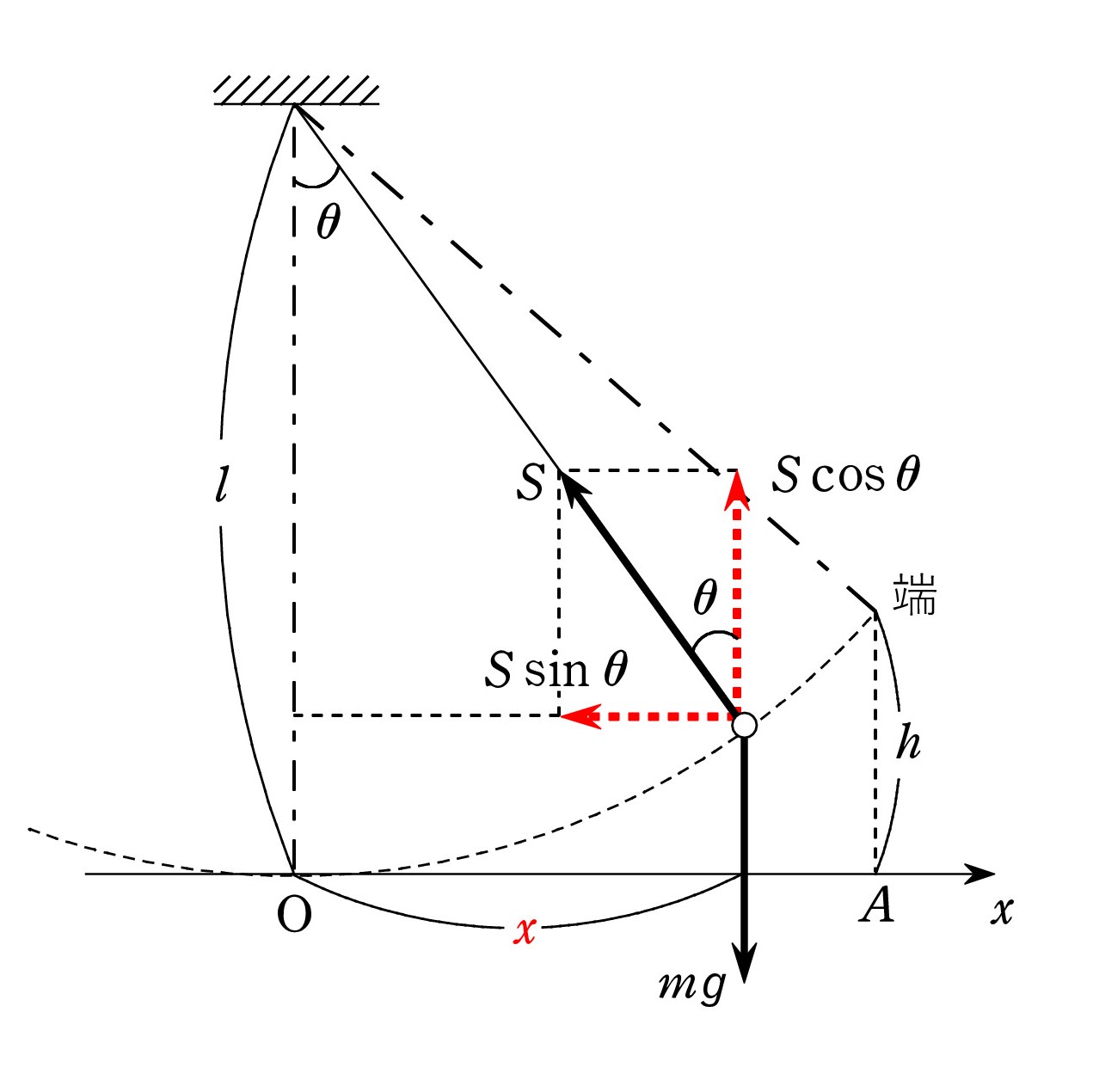　図のように、点Ｏを原点として水平にｘ軸をとり、水平方向の運動に着目します。
重力は鉛直方向なので、関係がなく、張力Ｓの水平成分 Ｓsinθ が復元力Ｆになります。　この段階から見方がガラッと変わっています。

　そして、半径方向について、遠心力を考えてのつり合いは　　　　Ｓ ＝ ｍｇcosθ ＋ ｍｖ²/ｌ　
　振幅Ａが小さいとｖも小さく、遠心力の項が無視でき (※)、　　　Ｓ ≒ ｍｇcosθ
こうして　　　　Ｆ ＝ Ｓsinθ ≒ ｍｇcosθ sinθ　
　図より　sinθ ＝ ｘ/ｌ で、
θ が微小のとき、　cosθ ≒ １　なので、　　Ｆ ≒ ｍｇｘ/ｌ
　Ｆ ＝ Ｋｘ の形ですから、単振動であり、周期Ｔが出せるのは先ほどと同じです。
　Ｆに符号を含ませれば、　Ｆ ＝ −Ｋｘ　　座標ｘの正負によらず成り立ち、単振動を保証する重要な式 です。　マイナス符号が復元力に対応しています。

　遠心力の項を無視したことと cosθ ≒ １ としたことで、近似が二度になっています。
できれば、近似は一度ですませたいのです。　真の値からどの程度ずれるかが評価しやすいからです。　それが曲線座標が好まれる一つの理由です（運動の軌跡に沿うことが最大の理由)。

(※)　振動の端での高さをｈとし、点Ｏでの速さをｖ_max とすると、エネルギー保存則より
　 1/2・ｍｖ²_max ＝ ｍｇｈ　　よって、遠心力 ｍｖ²/ｌ ≦ ｍｖ²_max/ｌ＝２ｍｇｈ/ｌ
　Ａが小さく、　ｈ≪ｌ　　したがって、遠心力は ｍｇcosθ に比べて無視できる (cosθ ≒ １)。


　Ｓを調べるのに、別のルートもあります。　鉛直方向にはほとんど動かないので、力のつり合いから　Ｓcosθ ≒ ｍｇ とし、　cosθ ≒ １ を用いて、　　　Ｓ ≒ ｍｇ
　復元力は　　　　Ｆ ＝ Ｓsinθ ≒ ｍｇsinθ ＝ ｍｇｘ/ｌ＝ Ｋｘ
　先ほどより簡便です。　ただ、出発点の、鉛直はつり合いという近似がどの程度いいのか、定かではありません。




Q10.　納得しました。　やはり、水平・鉛直に分解して考えるなら、水平ｘに対しては、重力は直接には関係しないですよね。
　この間、自分でもいろいろな参考書を調べてみました。　その中に「重力と張力Ｓの合力は円の接線方向を向き、ｍｇsinθ となる」という記述がありました。　これなら ｍｇsinθ　には Ｓ の寄与も含まれ、円弧のｘを水平ｘに置き換えても「トリッキー」でなくなると思います。


A.　その記述は近似として正しいだけです。　合力が接線方向を向くのなら、半径方向は力がつり合い、 Ｓ ＝ ｍｇcosθ　となるはずですが、正しくは　Ｓ ＝ ｍｇcosθ ＋ ｍｖ²/ｌ　です。　合力が接線方向を向くのは ｖ＝０ となる端の位置だけですね。
　円弧に沿って運動するので、合力がその向きに働くというのは、いかにももっともらしく、多くの人が受け入れていますが、厳密に成り立つわけではないのです。

　とはいえ、近似としてはＯＫですので、「トリッキーでなくなる」のはその通りです。


　頭が痛くなってきたでしょうね。　要するに、水平・鉛直でもできますが、円弧に沿った座標軸の方がはるかにスッキリしているのです。　曲線のように「頭を柔らかく」することですね。
　単振動は 等速円運動の正射影として定義されているので、直線運動だという主張はもっともなのですが、定義を拡張した方が窮屈でなくなるのです。
　円弧を重視する教科書は多いのですが、曲線座標軸を前面に出していないので、どこか歪み(ゆがみ)を感じさせる記述になっています( やや 皮肉を込めて！)。

Q11.　 単振り子は 入試ではあまり重要ではないようですが・・・


A.　確かに、教科書でも入試でも、ばね振り子に比べて 単振り子は影の薄い存在です。
　ばね振り子は単振動として純正ですが、単振り子は近似を必要とするなど、雑種的です。　でも、雑種の方が多様性に富むというか、物理としての奥行きや広がりがあり、いろいろと学ぶことの多い素材なのです。

　昔は実用性もありました。　振り子時計は、振り子の周期が一定であるのを利用したものです。
　時計の進み・遅れは 振り子の長さｌで調節します。　その頃よく見かけた問題です。　

　　　時計が進み過ぎるとき、振り子の長さは 長くすべきか、短くすべきか？

　日常出会わなくなったお陰で予備知識がなく、定性的な考察力が問われています。

　　　　・・・・・・・・？・・・？・・・？・・・？・・・？・・・・・・・・





Q12.　 チック・タックというテンポを遅くしてやれば、時計の針がゆっくり進むでしょうから・・・周期Ｔを長くしてやることですね。
　Ｔ＝2π √(ｌ/ｇ) から、長さｌを長くすればいいことが分かります。


A.　その通りです。　では、

１日に１分進む振り子時計の場合、振り子の長さをどのくらい長くすればいいですか？

　今の長さに対する割合で答えて下さい。　１/100 とか ３/5000 とかといった具合に。　｜x｜≪１　のとき、　(１＋ｘ)ⁿ ≒ １＋ｎｘ　としていいです。
　こんどは 計算力が試される問題です。　腕に覚えのある人は挑戦してみて下さい。

　　　　　　　　　　　　　　　　　　　　　　　　　　　　解答（※X3※）は最後に

Q13.　 ほかにも単振り子についての話題とか、ありますか ？


A.　以下は雑談です。　いつか模試の問題にと思っていたことです。

　もし、未知の天体に連れて行かれたとしたら・・・という仮定での問題です。
　その天体について調べたいのです。　一様な球体で、自転はしていないとします。

　まず、適当な長さｌのひもに小石を結び付けて、振り子の周期Ｔを測れば・・・
　　・・・重力加速度ｇが分かります。
　　　　　　　　　　　　　　　　　　　　　（ Ｔ＝2π √(ｌ/ｇ) → ｇ＝４π²ｌ/Ｔ²)
　さらに、その天体の半径Ｒが分かれば・・・
　　・・・天体の質量 Ｍ が分かります。
　　　　　　　　　　 　　　( ｍｇ＝ＧＭｍ/Ｒ² → Ｍ＝ｇＲ²/Ｇ　Ｇ：万有引力定数 )

　　・・・そして、天体の密度 ρ が分かります。
　　　　　　　体積Ｖ ＝ 4πＲ³/３　であり、　　　ρ ＝ Ｍ/Ｖ ＝ 3ｇ/(4πGR)

　もう気が付いているかもしれませんが、以上は、地球についての知見の歴史を大まかにたどっています。　万有引力定数Ｇを確定したのがキャベンディッシュの実験ですが、キャベンディッシュ自身は 地球の密度 ρ を求めることが目的でした。

　なお、重力加速度ｇは自由落下で調べるのが素直ですが、単振り子の方が精度よく求められます。　空気抵抗の影響を受けにくいことと、現象がゆっくりしている上に 繰り返しが利用できて 時間が計りやすいためです。


　模試の問題としては、上のように誘導すれば標準レベルですが、難化させたければ、途中をカットすることになります。
　振り子の長さｌ、周期Ｔ、天体の半径Ｒ を与え、「 天体の密度 ρ を求めよ」とすれば、筋道を全部 自分で構成する必要が生じます。　答えは　ρ ＝ 3πl / (GRT²)　ですが、振り子のおもりの質量 ｍ や振幅Ａをまやかしに与えるかもしれません。　必要のない量を余分に与えることで難度が上がります。

　もつれた糸をほどく時のように「まず、何が分かるか？」と考え始めるのが鉄則 です。
もちろん、「すると、次に何が分かるのか？」と、論理の鎖 が続きます。
「答えにたどり着くためには 何が分かればよいのか」と逆方向から考えるのも有力 です。　ρ を求めるためには 質量Ｍが分かればよい、というふうに。
　論理の鎖は両側から伸びて、やがて一本になる――という手法です。　幾何学の証明でよく言われていることです。

　また、長文問題にしたければ、この Dialogue で扱ってきた単振り子の理論や実験の設問などを 派生的に取り入れることで できます。　天体から万有引力の諸問題につなぐのはさらに容易です。
　長文問題の対策を尋ねられることがありますが、標準問題をきちんと身につけておくのがベスト です。　上で述べた「論理の鎖」も 基本問題や標準問題という短い鎖をつないで長くしていくのです。




Q14.　「天体の半径Ｒが分かれば」とありますが、Ｒはどのようにして求めるのでしょうか。　天体を外から観測すれば分かるでしょうが、今は天体に降り立っての話と思います。　また、簡単に一周できるような小さな天体ではないとしてです。




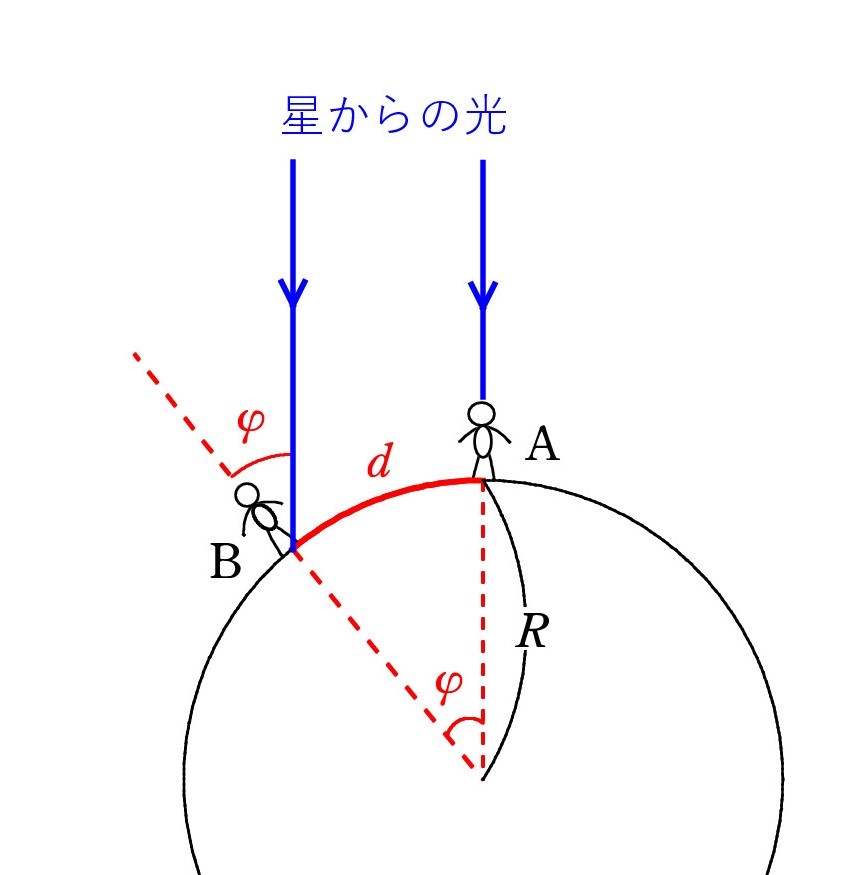A.　半径Ｒは 比較的測りやすい量です。　ある地点Ａで ある星が真上(天頂)に見えた時、地点Ｂでは真上から少しずれて見えます。ずれの角度を φ とし、ＡＢ間の距離（実は円弧の長さ）をｄとすると、Ｒφ＝ｄ となるからです。

　古代ギリシアのエラトステネスは太陽を利用して地球の大きさを導きました。　地球が丸いからだと原因を見抜いていたこと自体がすばらしいのですが、かなりの正確さで大きさを決めました。
　地点Ａで深い井戸の底に太陽が差し込んでいるとき（すなわち、真上にあるとき）、地点Ｂで地面に棒を垂直に立てると、少し影ができます。それから φ が分かりました。　tanφ＝(影の長さ)/(棒の長さ) ですが、棒の先と影の先を糸や棒で結んで直接角度 φ を測った方が簡単です。
　ただし、地球は大きいので、φ が測れるようにするには、ＡＢ間は何日もかかって移動するような距離をとり、「同時に」観測する必要がありました。　夏至の日の南中を利用したとのことです。　ここで、地学か地理に詳しい人なら、地点Ａはある特別な場所であることに気づくかもしれません。　何と呼ばれる線上にあるでしょう？

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　解答（※X4※）は最後に

Q15.　 天体の密度 ρ に話が及んでいましたが、大切なのは 天体の質量 M が求められることだと思います。　実際問題として、地球以外の天体の質量はどのように測っているのでしょうか？　 そこに行くことができたのは月だけです。　探査機を送れた惑星も限られています。


A.　天体の質量 M は、その天体の周りを回る別の天体Ｐの運動で決めています。
　簡単のために、Ｐは等速円運動をし、半径ｒと、周期Ｔが観測できたとします。

　　　　　Ｍ を、ｒ と Ｔ を用いて表してみてください。 （万有引力定数Ｇ）

　　　　・・・・・・・・？・・・？・・・？・・・？・・・？・・・・・・・・




　Ｐの質量を ｍ とすると、　遠心力と万有引力のつり合い（あるいは運動方程式）より
　　　　　ｍｖ²/ｒ ＝ ＧＭｍ/ｒ²　　　　∴　ｖ ＝ √(ＧＭ/ｒ)
　すると、周期 Ｔ ＝ ２πｒ/ｖ ＝ ２π√(ｒ³/ＧＭ)　　　　　∴　Ｍ＝4π²ｒ³/ＧＴ²

　Ｐの質量 ｍ は分からなくてもよいことに注目してください。
　また、楕円軌道でも求められます。

　太陽の質量は地球の運動から求めることができ、惑星の質量はその周りを回る衛星の運動から求められます。
　ただし、この方法では衛星の質量は分かりません。　衛星を回る人工衛星を用意してもいいのですが、実際には、衛星の近くを通った探査機の軌道の曲がりで調べています。
　地球の質量も人工衛星を利用するのが最も正確です。

　太陽系を離れた恒星になると、その周りを回る惑星は暗過ぎて観測できません。　そこで、連星と呼ばれる２つの恒星を利用します。　重心Ｇを中心として、共に円運動(あるいは楕円運動)するので、それぞれの質量を調べられます。 ２つの星はＧを挟んで向かい合うので周期は同じになります。　なお、連星は珍しいものではありません。
　では、問題にしてみます。

重心の周りで円運動する２つの恒星がある。　周期はＴで、軌道半径はｒ₁とｒ₂である。　星の質量 Ｍ₁ と Ｍ₂ を求めよ。

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　解答（※X5※）は最後に




Q16.　 地球の大きさや質量についての 歴史的な話で思い出しましたが、地球の自転も振り子で実証されたと聞きました。


A.　「フーコーの振り子」ですね。　振り子が長い間振動できるようにしておくと、振動方向が徐々に変わっていきます。具体的には、振り子の振動面が回転していきます。
　極（北極か南極）が分かりやすいでしょう。　振動面は宇宙空間に対して不変なので、地球上で見ると、回転するのです。極以外でも見られます。　では、

　北半球では振動面はどちらに回転するでしょうか。　振り子を上から見下ろしたとき、
　時計回りか、反時計回りかを答えて下さい。　また、南半球ではどうなりますか ？

　　　　　　　　　　　　　　　　　　　　　　　　　　　　解答（※X6※）は最後に

Q17.　自転に関して確認しておきたいことがあります。　Q13 の「未知の天体」の話で、自転していないという条件がありましたが、自転していると、緯度によって重力加速度が変わってくるからですね。


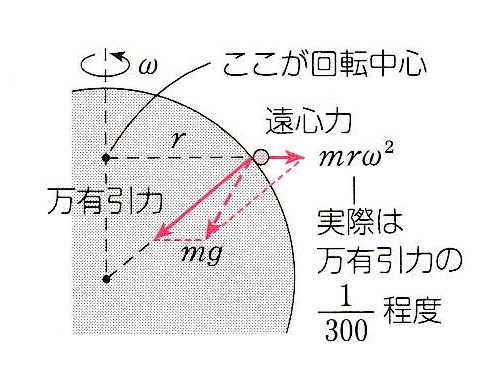A.　その通りです。　我々は地球と共に回転していて、言わば回転座標系にいます。　　そこでは慣性力として　遠心力　ｍｒω² ＝ ｍｖ²/r　が働くことが大切です。
　そのとき、ｒは回転軸からの距離を用意することも忘れないでください。　地球なら、自転軸(地軸)からの距離です。　万有引力と遠心力の合力が 重力 ｍｇ です。

　図から、重力加速度 ｇ は 極で最大、赤道で最小になることが理解できます。（万有引力 ＧＭｍ/Ｒ² は一定で、遠心力 ｍｒω² は赤道で最大かつ逆向き）


　フーコーの振り子で、振動面を回転させる力が働いているように見えるのも、回転座標系にいるために現れる慣性力の一種で、コリオリの力と呼ばれています。　物体の速度に比例し、速度に垂直に働きます。　北半球では右に向きを変えようとします。　振動するおもりはわずかずつ右にそれ続け、結果として、振動面が回転していくのです。
　
　以上をきちんと理解するには、静止系での運動方程式が 回転座標系ではどのように書き換えられるかを確認する必要がありますが、大学に行っての話になります。
　回転座標系での慣性力は、遠心力とコリオリの力の２つです。　物体が(座標系内で)静止していれば、遠心力だけですみます。
　



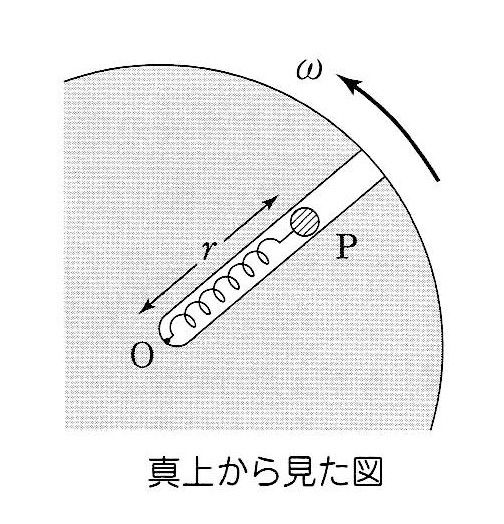Q18.　回転軸と遠心力との関係 で思い出しました。
　図は「森」の問題38のものですが、水平に角速度ωで回転する円板には溝が掘られ、なめらかな溝に沿って ばねに結ばれた 質量 ｍ の小球Ｐが振動します。
　円板上で静止している観測者にとって、Ｐには遠心力 ｍｒω² が働くとして解答がなされています。　今まで遠心力は円運動に対して考えてきました。　円板は円運動ですが、Ｐの運動は振動が加わるので、円運動ではありえません。　遠心力の扱いが今までと少し違うような気がしますが・・・
　また、観測者は円板上のどこにいるかが 問題文に書いてありませんが・・・


A.　疑問に思わない人が大半ですが、よく気が付きましたね。
　確かに、遠心力の導入時には、等速円運動する物体と共に動く観測者を想定していました。　速さの変わる円運動でも、Q1 で見たように、半径方向に限定されただけで、大差はありません。　このような「物体と共に円運動する観測者」ではなく、単に円板上で静止している観測者ですから、飛躍しているのはその通りです。　「観測者の加速度を調べてから 慣性力を」という原則も踏み外していますね。

　ただ、上で述べた回転座標系では 次の定理が確認されているのです。

　「 遠心力は、物体の運動によらず、 回転軸Ｏからの距離ｒに応じて、半径方向外向きに ｍｒω² となる。」

　この定理のお陰で、いくつかの物体が円板上にあっても、それぞれに対して遠心力が簡単に用意できます。　物体ごとに観測者を考える(変える)必要がなくなっている のです。

　 円板上で静止している誰にとっても、円板に対するＰの運動は同じなので、観測者は円板上のどこにいてもよいのです。　中心Ｏにいると思うのが分かりやすいでしょう。 距離ｒの測り方にも迷わないと思います。(＊1)

　このような回転円板上での力学は入試ではよく取り上げられています。　本当は高校の範囲を超えているのですが、当然のごとく出題されます。
　

　なお、溝を用意しているのは、コリオリの力によって軌道が曲げられるのを防ぐためですが、これは出題者だけが気にすればよいことです。(＊2)



(＊1)　点Ｏを原点として、円板上にｘ軸とｙ軸をとり、円板に垂直に(回転軸方向に)ｚ軸をとったものが、回転座標系である。　円板上のどこを原点としても、円板に対して静止していれば 同等の回転座標系となる。
　回転する板であれば、円形である必要はなく、さらには、地球のような回転する立体でもよい。
　

（＊2） とは言え、回転円板上ならコリオリの力（コリオリ力）が納得しやすいので、以下、ふれておこう。

　静止系において物体が中心Ｏから半径方向外向きに等速直線運動すると、円板上の軌跡は曲線になるのは当然であろう。　そして、曲線は進行方向に対して右にカーブすることに注意したい。
　反対に、中心Ｏに向かって等速直線運動しても、軌跡は右カーブの曲線になる。　少し分かりにくいので、時間間隔を一定にした図にプロットして確認するとよい（☆)。

　いずれも、円板上の観測者はコリオリの力が速度の向きに対して右向きに働いたからと考える。
　以上、地球上では 北極の状況に対応し、フーコーの振り子の話につながる。

　ここで半径方向の運動を取り上げたのは、考えやすさのために過ぎない。


　☆　回転円板上での軌跡
　　　（入試には無関係です）







＃＃＃＃　Dialogue はここまで　＃＃＃＃

＃＃＃　Dialogue （対話）：　Q1 〜 Q10　＃＃＃＃＃

　　――――――　単振動　・　Ｆ＝−Ｋｘ　・　エネルギー保存則　――――――



Q1.　振動が起こりそうだが、単振動になるかどうか分からないときは合力 F を調べるのでしたね。　物体の位置座標 x を用いて、 F = −K x と表せたとします（K：正の定数)。
　問題はその後の論理の進め方です。　ある本では、運動方程式 m a ＝ F から加速度 a を求め、単振動の公式　a ＝ −ω² x 　と見比べて 単振動であることを確認し、角振動数 ω を決め、周期を　T ＝ 2π/ω　で求めるように書いてあります。（ π：パイ、円周率 ）　　模試の解説でもそうなっていました。
　ところが、「風」や「森」での論理はこうはなっていません。　説明していただけませんか。


A.　まず、確認ですが、座標軸の原点 x = 0 は力のつり合い位置としての話ですね。
　F = −K x なら、単振動と断定できます。　そして、周期は　T = 2π√(m/K)　としていいです。　加速度 a ＝ −(定数)ｘ に至った段階で 単振動と分かるというのは まだるっこい のです。　力 F の段階で分かることです。 力が運動を決める からです。 それこそが運動方程式の主張ですね。

　大学で微分方程式を習うと、 a = −ω² x　の形を好むようになります。　a は ｘ の２階の時間微分であり、 解は　ｘ ＝ A sin ωt ＋ B cos ωt　あるいは　ｘ ＝ A sin (ωt ＋ θ₀)　になると言えるからです（ A、B 、θ₀ は任意の定数)。
　高校の教科書では、単振動なら、F ＝−K x になることは示されていますが、その逆が示されていません。　微分方程式の知識が必要だからです。　ただ、それは一度確認すれば 済むことです。　毎回たどる必要はありませんし、微分方程式を習っていない段階では 無意味に等しい回り道でしょう。




Q2.　これからは「 F = −K x　なら、単振動。　周期は　T = 2π√(m/K) 」という方針で対処します。　　a ＝ −ω² x　は不要と思っていいのでしょうか。


A.　それはそれで役に立ちます。　入試の出題者は、当然ながら大学の先生であり、微分方程式が頭にあるため、加速度 a を求めるように誘導してくることが珍しくないからです。　a ＝ −(定数)ｘ という形を見たら 単振動と判断できるように。　定数は 正の値で、ω² を表します。　その場合は、ω から周期Ｔへというルートで対応します。

　ω が決まると、時間変化を式にしたい場合には便利です。　たとえば、振動中心から動き出せば、ｘ＝± A sin ωt であり、振動の端からスタートすれば、ｘ＝ ± A cos ωt　のように（時間変化のグラフを脳裏で描いて)。
　そして、速度 v は　ｖ ＝ dx/dt　で、加速度 a は　a ＝ dv/dt　と、微分で対処できます。　a ＝ −ω² x なら、ダイレクトにｘから a に移れますし、チェックにも使えます。

　Ｋと ω の関係は 覚えておくか、すぐに出せるように。　ω ＝ 2π/Ｔ ＝ √(K/m)
Ｔの表式で (2πをはずし)平方根の中身をひっくり返す――という覚え方もあるでしょう。

Q3.　ほかに注意点はありますか？


A.　　F＝−K x の K は周期 T を決めるほかにもう一つ大切な役割があります。
　単振動の位置エネルギーですね。　合力Ｆに対する位置エネルギーなので、合力の位置エネルギーとも呼ばれます。
　単振動のエネルギー保存則　m v²/２ ＋ K x²/２ ＝ 一定　が成立します。　ｘ は座標ですが、２乗して符号は関係なくなるので、振動中心からの距離と覚えた方が扱いやすいでしょう。　　この保存則の有用性は 強調しても し足りません。

　たとえば、鉛直ばね振り子の場合、つり合い位置Ｏを原点(ｘ＝０)にすれば、弾性力と重力の合力は、ばね定数をｋとして　Ｆ＝−ｋｘ と表され、Ｏを中心として単振動することが分かります（エッセンス（上）ｐ82 (新版は p84)）。　したがって、周期Ｔは水平ばね振り子と変わらず、単振動のエネルギー保存則は 　m v²/２ ＋ ｋx²/２ ＝ 一定　となります。
　Ｋ＝ｋ の ケース という認識の下で使用してほしいですね。　ｋx²/２ は弾性エネルギーではありません！　周期も、T = 2π√(m/K) に基づいて、T = 2π√(m/ｋ) が存在しているのです。

　重力の位置エネルギーが顔を出さないのが、初心の頃は不思議だったはずです。　今では 重力はＦに含まれているからと納得しているはずですね。
　(自然長を基準位置にした)弾性エネルギーと 重力の位置エネルギーの２つを考える 普通の力学的エネルギー保存則 に比べて、ずっと簡単な計算ですみます。
　斜面上のばね振り子でも同じことでした。




Q4.　ばね振り子での 単振動のエネルギー保存則の威力は実感しています。
　浮力による単振動など 一般的に用いられる のも驚きでした。　浮力などの仕事を考える必要がないのですから。
　単振動の位置エネルギーには エネルギー保存則以外の用途もあるのでしょうか。


A.　問題にしてみます。

単振動は、つり合い位置で静止している物体を、距離Ａだけ移動させて、放すというケースが多いのですが、移動させるのに必要な仕事はいくらですか？　復元力は　F＝−K x とします。



　　　　・・・・・・・・？・・・？・・・？・・・？・・・？・・・・・・・・



　単振動が始まるときの最も素直なケースです。　　つり合い位置は振動中心 で、放した位置が端になるので、振幅Ａの単振動が始まります。

　必要な仕事は、単振動の位置エネルギーの増加分 を確認すればよいので、 KＡ²/２ ですね。　初め 振動中心での単振動の位置エネルギーは０です。基準点ですから。　いくつもの力が働いていても、まるで気にならないのです。

　格式張って言えば、非保存力の仕事＝力学的エネルギーの変化 を用いています。
左辺は外力の仕事で、静かに放しているので、右辺は位置エネルギーの変化です。
外力の仕事＝位置エネルギーの変化 の形はよく出合います。
　



Q5.　物体が位置座標 ｘ にいるときの合力Ｆを調べる際、ｘ＞０ と ｘ＜０ に場合分けする必要があるのでしょうか？
　また、ｘ 軸の原点が振動中心になっていないときはどうなるのでしょうか？　力のつり合い位置が押さえていないときなどに起こります。


A.　合力 F を調べるときには、物体が正の位置 ｘ にいるとして考えるのがコツです。 　ｘ が負でも成り立つことは 普段の勉強ではしてください。入試では飛ばします。　二通りの可能性があるときは、分かりやすい方を選べ です。
　式というのはありがたいもので、ｘの正負に関わらず成り立つのがふつうです。　数学のように場合分けが必要になるケースはまれです。

　座標原点が振動中心になっていないと、　 F ＝ −K x ＋ C　の形になりますが、
　 F ＝ −K（x − C/K） と変形することにより、 ｘ ＝ C/K　を中心とする単振動と判読します。　　x − C/K ＝ Ｘ と置き直し、 F ＝ −KＸ とすると、ていねいですが。
　加速度 a = −ω² x ＋ C　も同じようにして、 ｘ ＝ C/ω²　を中心とする単振動です。
　　　　　　　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（C：定数）

Q6.　座標軸ｘを設定して、 Ｆ＝−Ｋｘ を調べるのが本格的 だとは思いますが、 単振動かどうかの簡便な調べ方はないのでしょうか。


A.　つり合い位置から少しずらすと、元に戻るようなら、つまり、復元力が働くようなら、振動が起こります。そして、ずれの距離ｘに比例した復元力なら、単振動です。
　もともと力がつり合っていたので、アンバランス分が合力Ｆで、それに注目すればよいのです。

　たとえば、鉛直ばね振り子の場合、下に 距離 ｘ ずらすと、復元力は ばねの弾性力の増加分で ｋｘ です（重力は一定 )。　よって、単振動で、周期は　T = 2π√(m/k)
　念のためですが、つり合い位置での ばねの伸びをｄとすると、 弾性力は ｋｄ から
ｋ(ｄ＋ｘ) になっていて、増加分は ｋｘ です。　　　　 （ ｋ：ばね定数、　ｍ：振り子の質量 ）

　斜面上のばね振り子でも同じことです。　ｍｇ sin θ は 一定で、周期に関係しないのです。
　一般に、弾性力以外に 一定の力がかかっても、周期は　T = 2π√(m/k) で不変 ということまで納得できるでしょう。　一定の力は つり合い位置(振動中心)を変えるだけですね。




Q7.　ばね振り子以外の例も挙げて頂けると、助かりますが・・・


A.　　浮力による単振動を取り上げてみます。
　水に浮かぶ 円柱や直方体などの柱体が上下に振動する場合です。つり合い位置から ｘ だけ余分に沈むと、水に浸かっている体積が Ｓｘ だけ増え、浮力が ρ(Ｓｘ)ｇ 増します。これが復元力で、単振動になり、Ｋ＝ρＳｇ より 　周期 T = 2π√(ｍ/K)＝2π√ｍ/(ρSg)
　　　　　　　　　　　　　　　　　　　（ ρ：水の密度、　Ｓ：柱体の断面積、　ｍ：柱体の質量 ）

　以上、考えやすい方向に移動させているので、完全な論理とまでは言えませんが、手っ取り早いのが魅力です。

　一応、反対側への移動も確認しておきましょう。　鉛直ばね振り子のおもりを上へｘずらすと、弾性力が kx 減り、その分がやはりアンバランス分です。重力が優って、合力は下向きに kx です。
　また、水に浮く柱体を上にｘずらすと、浮力が ρ(Ｓｘ)ｇ だけ減って、重力が優り、合力は下向きに同じ大きさです。




Q8.　座標軸のもとで合力Ｆを調べる本格的な方法では、力のつり合い式が重要な役割をしていました。　たとえば、鉛直ばね振り子では、ｋｄ＝ｍｇ がつり合い式で、その位置（振動中心になるはずの位置）を原点として 下向きにｘ軸をとると、位置ｘでの合力は、
　Ｆ＝−ｋ(ｄ＋ｘ)＋ｍｇ＝−ｋｘ　という具合です。

　「アンバランス」に注目すれば、座標軸は必要なく、何よりつり合い式が不要になっているのが興味深いです。つり合いの状態は想像するだけですみますね。

　さて、だいたいの要領はつかめたと思います。　腕試しできるような問題はありませんか。


A.　では、問題 を３つ出してみます。

　いずれも 柱体Ｐの鉛直方向での振動で、浮力が関係しています。

　　　　　　　　　　　Ｐの振動周期を求めてください。

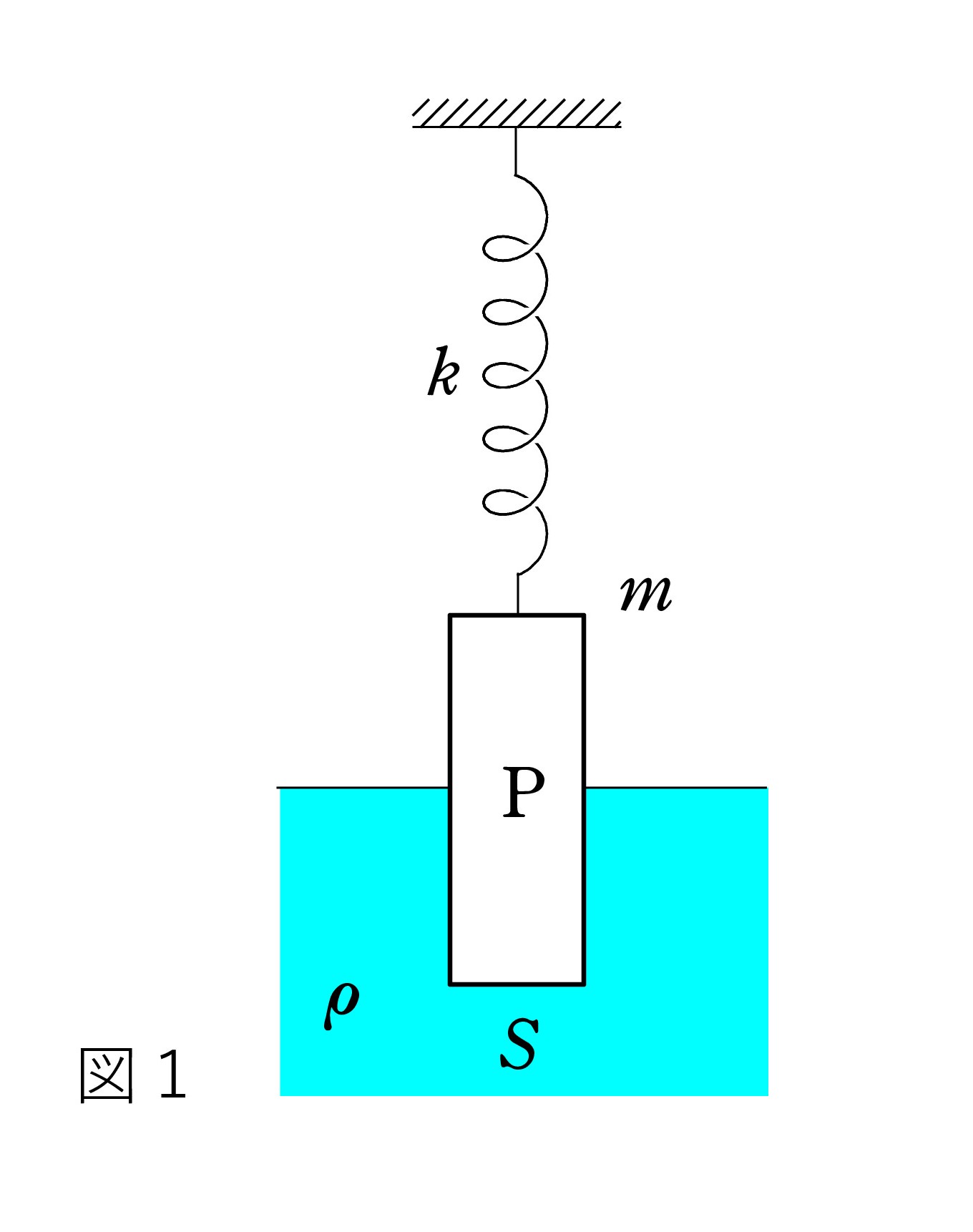
　Ｐの質量を ｍ、断面積を S、重力加速度をｇ とします。液面の位置は変わらず、図の状況での振動で、液体の抵抗は無視します。

　　図１：　Ｐは ばね定数ｋのばねに吊るされ、密度 ρ の液体に浮かんでいる。

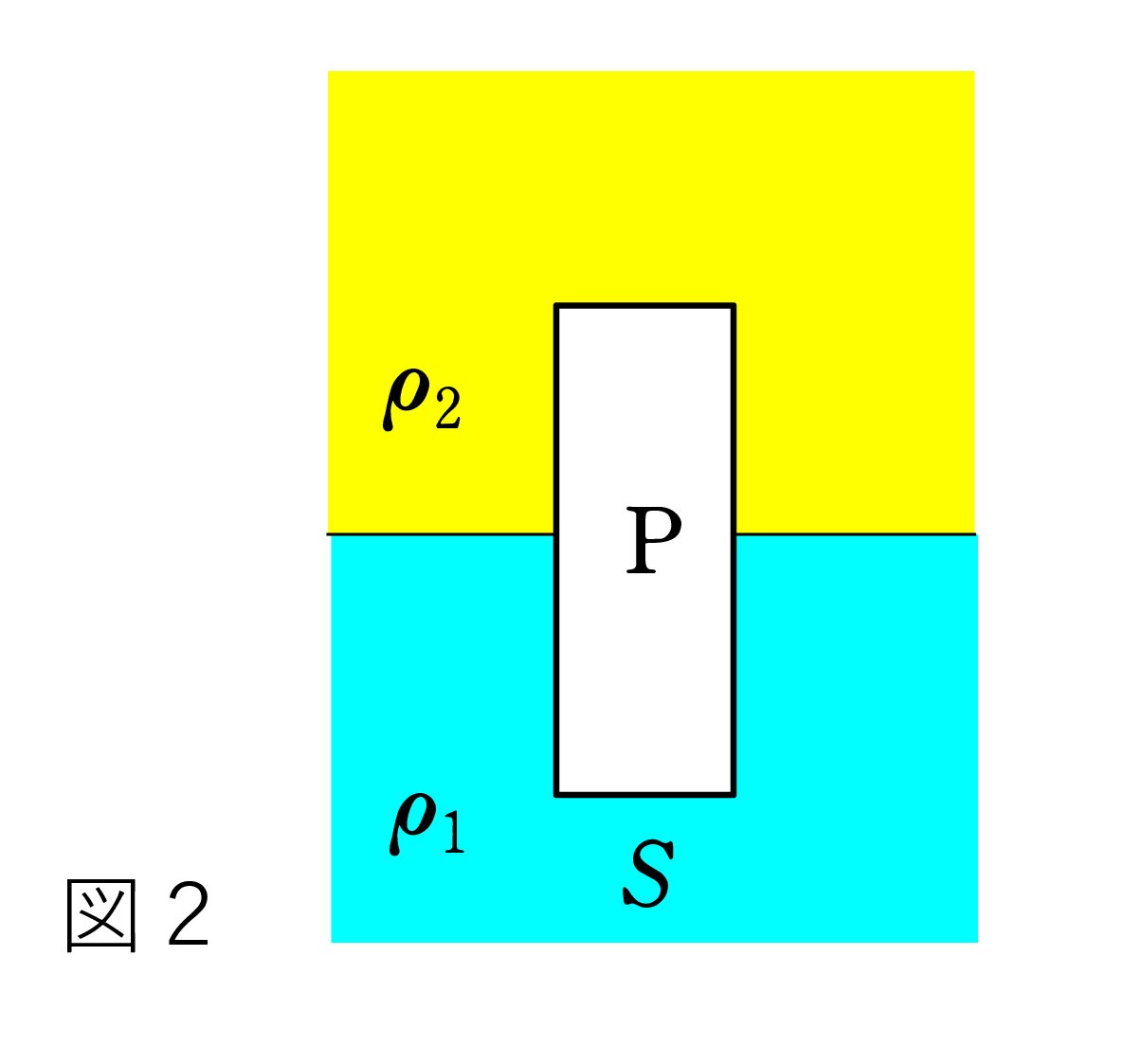
　　図２：　Ｐは 密度 ρ₁ と ρ₂ の２つの液体にまたがって浮いている（ ρ₁＞ρ₂) 。

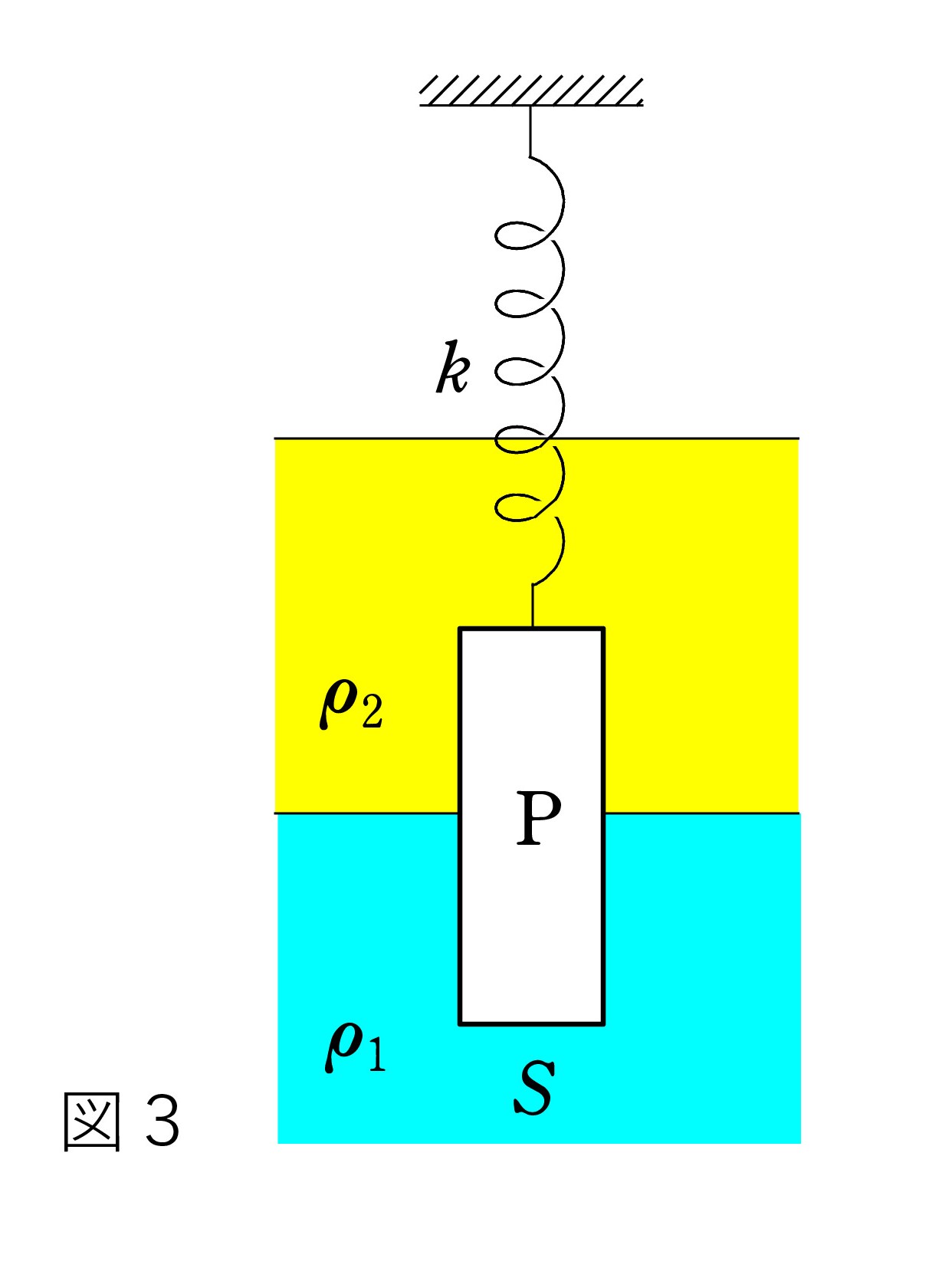
　　図３：　図２の状況に加えて、Ｐは ばね定数ｋのばねに吊るされている。

　　　　

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　解答（※Y1※）は最後に




Q9.　場合分けは大変ですね。　座標軸に基づく論理の方が場合分けが少ないということでしょうか。　ｘ≧０とｘ＜０で済みます。


A.　そうですね。　しかも、座標軸を選べば、場合分けは不要にできます。
　ばねの弾性力は、自然長の位置を原点にした座標軸では、−kｘ と表せます（自然長からの伸び・縮みに関係なく、座標軸の向きにも関係しない)。　他に重力など一定の力が働くなら、
　　　　Ｆ＝−kｘ ＋ 定数　　したがって、　Ｋ＝ｋ　

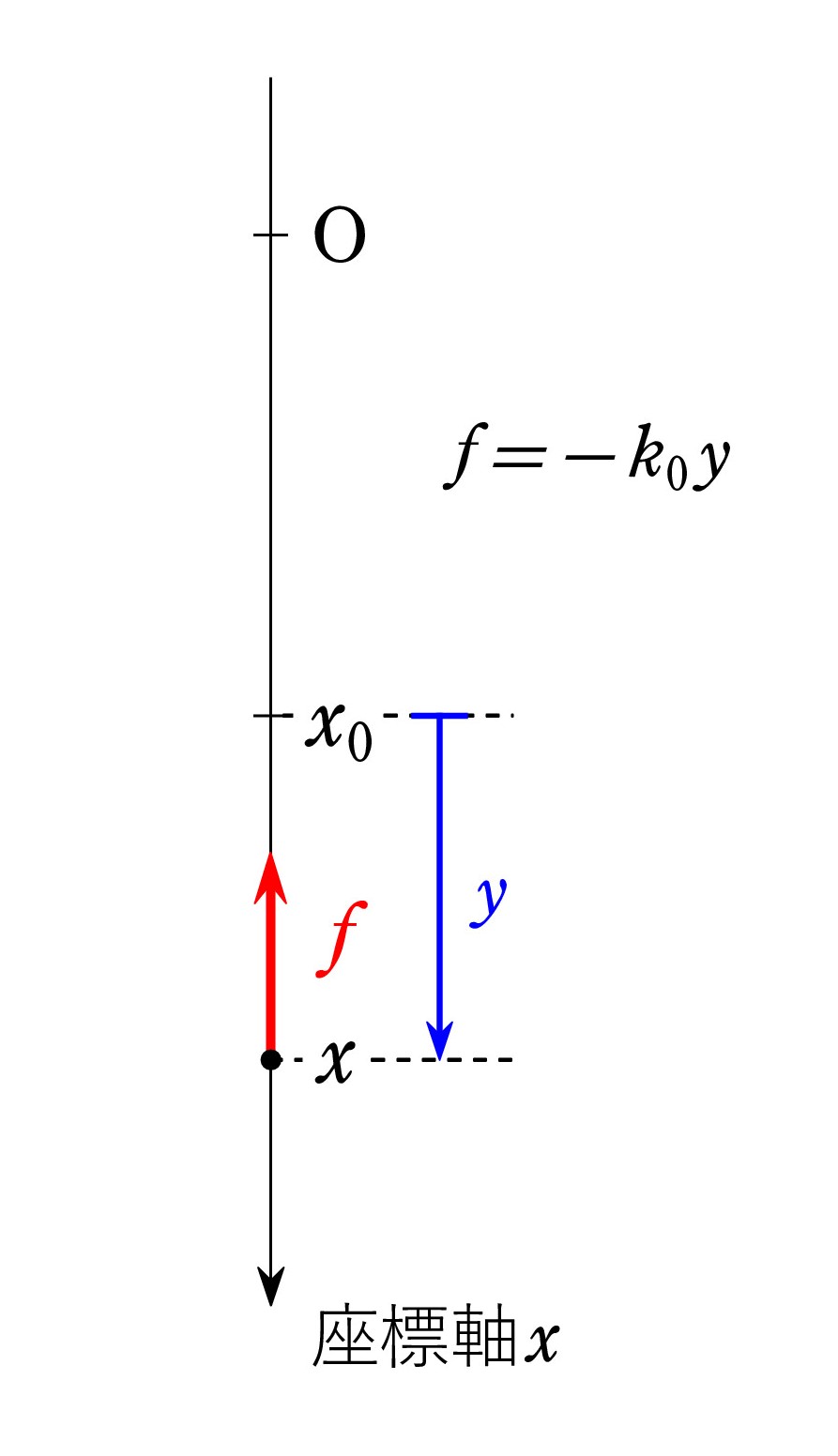　さらに、図１のように、浮力などの単振動を起こせる復元力 ｆ（比例定数ｋ₀ ) が加われば、
　　　　　　　Ｆ＝ −kｘ ＋ 定数 ＋ (−ｋ₀ｙ)
　ここで、ｘ＝ｘ₀＋ｙ であり、ｘ₀ は ｆ＝０ となる位置です。したがって、
　　　　　　　Ｆ＝−kｘ＋ 定数 −ｋ₀(ｘ−ｘ₀）
　　　　　　　　＝ −(ｋ＋ｋ₀)ｘ ＋ 定数 ＋ ｋ₀ｘ₀
　よって、　Ｋ＝ｋ＋ｋ₀　

　浮力の場合は、ｋ₀＝ρＳｇ です。




Q10.　なるほど。　式は式で強力ですね。
　一般化できませんか？　いくつかの単振動型の力が働くとき、それぞれの復元力の比例定数を K₁、K₂、・・・とすると、 K ＝ K₁ ＋ K₂ ＋・・・ が成り立ちそうに思えます。
　図１〜３の３つの問題を解いてみて 思いついたことです。


A.　その通りです。　それぞれの力が０になる位置を ｘ₁，ｘ₂・・・ とすれば、
　　　　　Ｆ＝ −K₁(ｘ−ｘ₁) ＋｛−K₂(ｘ−x₂)｝＋・・・
　　　　　　＝ −( K₁ ＋ K₂ ＋・・・)ｘ ＋ 定数
　よって、単振動で、　K ＝ K₁ ＋ K₂ ＋・・・　ですね。

　ばね なら　K₁＝ｋ で、ｘ₁ は自然長の位置、浮力なら Ｋ₂＝ρＳｇ で、ｘ₂ は 柱体Ｐの下面が液面になる位置です。　ｘ軸の原点は任意です。






＃＃＃＃　Dialogue はここまで　＃＃＃＃










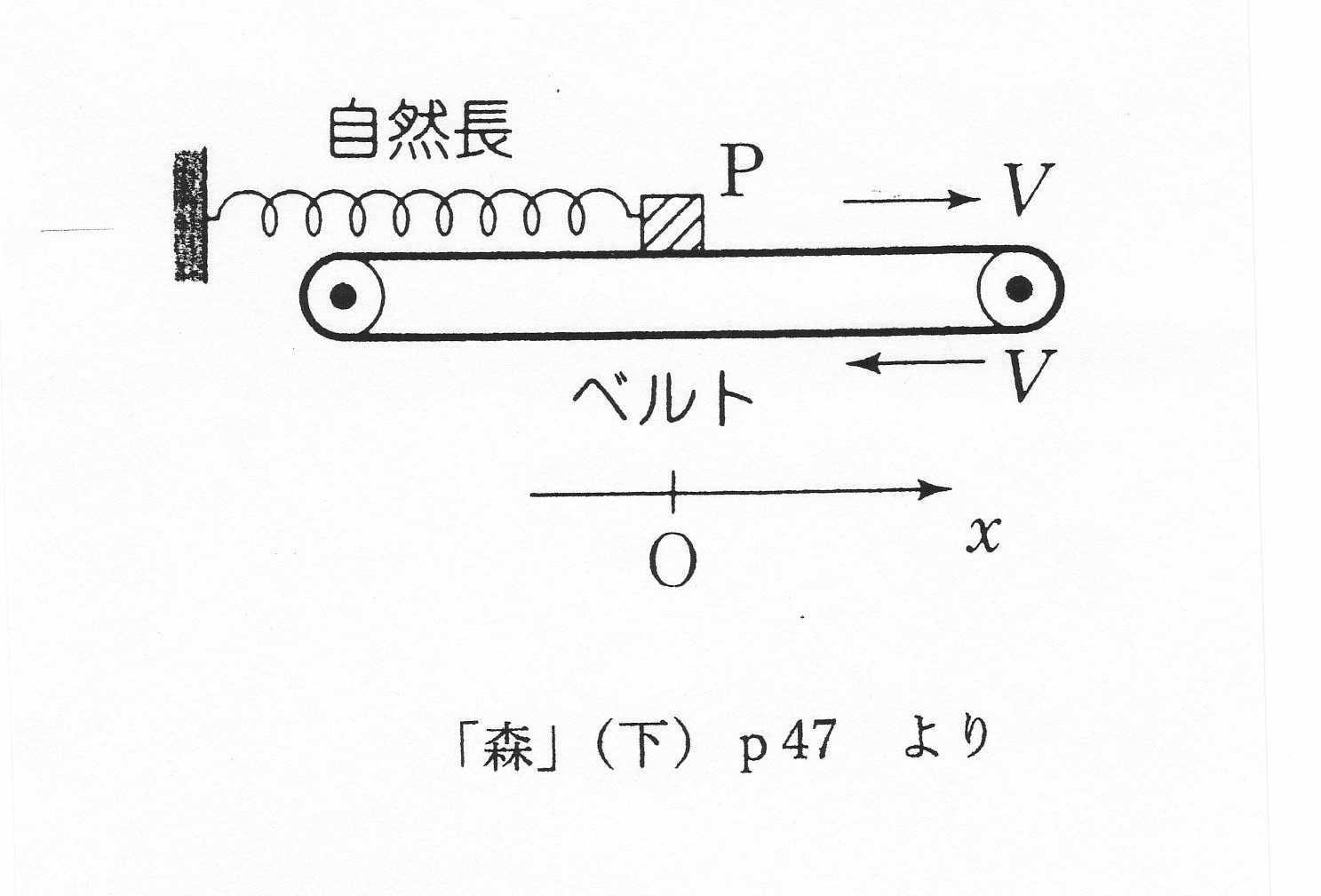Q.　ベルトコンベヤー上のばね振り子の場合、単振動するかどうか考えてみました。ベルトが図の V の 向きに速く動くとします。物体 P はベルトに対して常に左に滑るので、動摩擦力 μｍｇ は右向きですね。
　すると、自然長の位置を原点としたｘ軸上で、位置ｘでの合力 F は、
　　　　 F ＝ −ｋｘ＋μｍｇ ＝ −ｋ（ｘ−μｍｇ/ｋ）
　これで、運動は単振動で、振動中心は ｘ₀ ＝ μｍｇ/ｋ 、周期は普通のばね振り子と変わらないことが示せたと思います。まず、ここまで正しいでしょうか？
　正しいとすると、単振動のエネルギー保存則は成立しますか？　 動摩擦力が働くので、無理と思えますが・・・


A.　単振動の確認まで正しいです。動摩擦力の向きの判断も的確ですし、自然長を原点にしたので、弾性力は −k x と表せる という点もしっかり押さえられています。 F の表式から、この場合の K はばね定数 k ですね。

　そして、単振動のエネルギー保存則が成立 します。　このときの動摩擦力は、振動の向きによらず、大きさと向きが一定の力なので、保存力と同様に扱えるためです。　鉛直ばね振り子での重力と似ていると言ったら分かってもらえるでしょうか。　動摩擦力だから気になるのですが、物体にとっては単に一定の力がかかったのと同じことです。

　たとえば、ｘ＝ 3ｘ₀ で静かに物体 P を放せば、振幅 A は　A ＝ 3ｘ₀ ― ｘ₀ ＝ 2ｘ₀ です。 そして、位置 ｘ での速さを ｖ とすると、
　　　ｋ(2ｘ_０)² /２ ＝ ｍｖ² /２ ＋ ｋ(ｘ―ｘ₀)² /２ 　が成立します。
　最大の速さ v_max は、振動中心 ｘ ＝ ｘ₀ での　v_max ＝ 2ｘ₀ √(k/m)　ですね。 公式　v_max ＝ A ω　を用いてもいいです。

　摩擦熱が発生し、力学的エネルギーが失われていきますが、それはベルトコンベヤーまで含めて見たときの話です。摩擦熱の分はコンベヤーの駆動装置が担っています。 もちろん、物体もベルトも熱くなります。

　あるいは、単振動でエネルギー保存則の式が成立することは、三角関数を用いて一般的に示せるので、形式的に成立するのだという理解でもいいでしょう。　実際、θ＝ ωｔ＋θ₀ として、ｘ ＝ A sin θ、 ｖ＝ｄｘ/ｄｔ＝ A ω cos θ　であり、ω(＝2π/T)＝ √(Ｋ/m)　から確認できます（最後は sin² θ ＋ cos² θ ＝１ を用います)。　　　　　　（ π：パイ、円周率 ）

　摩擦のある平面上でばね振り子が振動すれば、減衰しますが、片道ごとは単振動で、やはりエネルギー保存則を適用していいです。　ただし、振動中心が行きと戻りで異なるので 要注意！（エッセンス（上）ｐ85 (新版は p87)）









Q.　面積速度が一定になるのは、ケプラーの第２法則ですが、万有引力による運動に限らないと聞きました。　ほかにどんな場合がありますか。


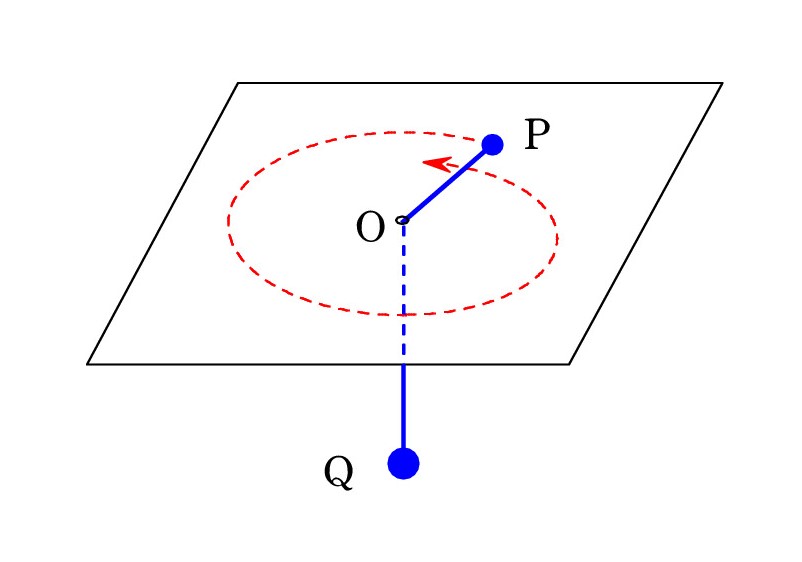A.　「力のベクトルが一点を指すとき、面積速度が一定になる」ことが証明されています。　惑星の場合には、万有引力が太陽という一点を指していました。　その他の例としては、図のように、Ｐ と Ｑ が糸でつながれ、Ｐ が滑らかな水平面上で回り、Ｑ が落下している状況です。　糸は水平面の穴 Ｏ を通っています。Ｐ の軌跡は螺旋的になりますが、糸の張力は一点 Ｏ を指すので、面積速度が一定になります。
　ただ、この知識は高校の範囲を超えるので、入試では誘導がなされ、必要な情報が与えられるはずです。

　大学では「角運動量保存則」という 回転に関する保存則 に出会います。　物体系が回転しながら収縮すると、回転が速く（角速度が大きく）なるというもので、フィギュアスケートの選手がスピンしながら広げていた腕を閉じていくと、回転が速くなるのはその例です。
　面積速度一定 は １つの物体についての 角運動量保存則 です。

　





Q1.　物理ではよく近似を用います。 やはり数学の厳密さには及ばないという気がしますが・・・


A.　数学がある決められたルール（公理）の下で議論しているのに対して、物理は自然を相手にしています。　一つの現象には様々な要素が関連してきます。そのうち何が最も大事なものなのかを取り出すのが近似の見方です。

　たとえば、地球が太陽の周りを回る軌道は、近似的には円です。等速円運動として扱うことが第１近似です。そうしてニュートンは万有引力の法則を導きました。実際の軌道も円にしか見えないでしょう。　第２近似としては楕円ということになります。これが厳密と思っている人が多いようですが（入試ではそれでいいですが）、実際には木星などの引力の影響で楕円からわずかに歪みます。つまり、どこまで行っても厳密解などないのです。

　必要に応じて近似の精度を高めるという重層的な見方をしています。　近似とは 本質を抉(えぐ)り出すこと です。




Q2.　現象の理解については、大まかな近似の方が優るということですね。　まず概要を把握して、次により詳細へと向かうわけですね。


A.　理解についてはその通りです。　どこまで詳細に押さえるかで言えば、実用目的に適した近似でいいとも言えます。

　今、皆さんが習っている力学はニュートン力学と呼ばれるもので、物体の速さ v が光速 c に近づくと、相対性理論に基づいた力学が必要になります。　月や火星・木星などに向かう探査機の速さ v は弾丸の速さよりずっと速いのですが、光速と比べれば微々たるものなので（ v ≪ c ）、探査機の軌道計算はニュートン力学によって決めています。　相対性理論による計算ははるかに膨大なものとなって大変なのに、出て来る結果の違いは無視できるからです。
　一方、加速器による素粒子の実験では、光速に近いので、相対性理論が欠かせません。　目的に応じた理論を用い、近似も必要に応じてということです。




Q3.　ニュートン力学はアインシュタインの相対性理論によって否定されたと聞いていました。


A.　 それはちょっと違います。　理論の発展は、螺旋階段を上がるようなもので、新たな理論は古いものを内に含みながら、より高いレベルになっています。　そして状況によっては、古い理論で十分ということが往々にして起こります。

　螺旋階段に例えたことで、階段を上るように少しずつ進展したかのような印象があるかもしれません。　一般の理論に対してはそれでいいのですが、ニュートン力学から相対性理論へは 飛躍と言っていい変化でした。　時間と空間に対する認識を変え、自然観を変えるほどのものだったのです。














熱　　//////////////////////////////////////////////////////////////////////////////////////////////



Q1.　理想気体の内部エネルギーの公式 Ｕ ＝ 3/2・ｎＲＴ は 単原子分子に対するもので、二原子分子には適用できないことを教わりました。 内部エネルギーは、気体を構成する分子の運動エネルギーの全量 であり、二原子分子では、分子の回転の運動エネルギーを考えなければならないからということでした。
　しかし、単原子だって、自転して回転の運動エネルギーがもてるのではないでしょうか？　１個の原子か、２個の原子かで大差がつくのは変だと思います。


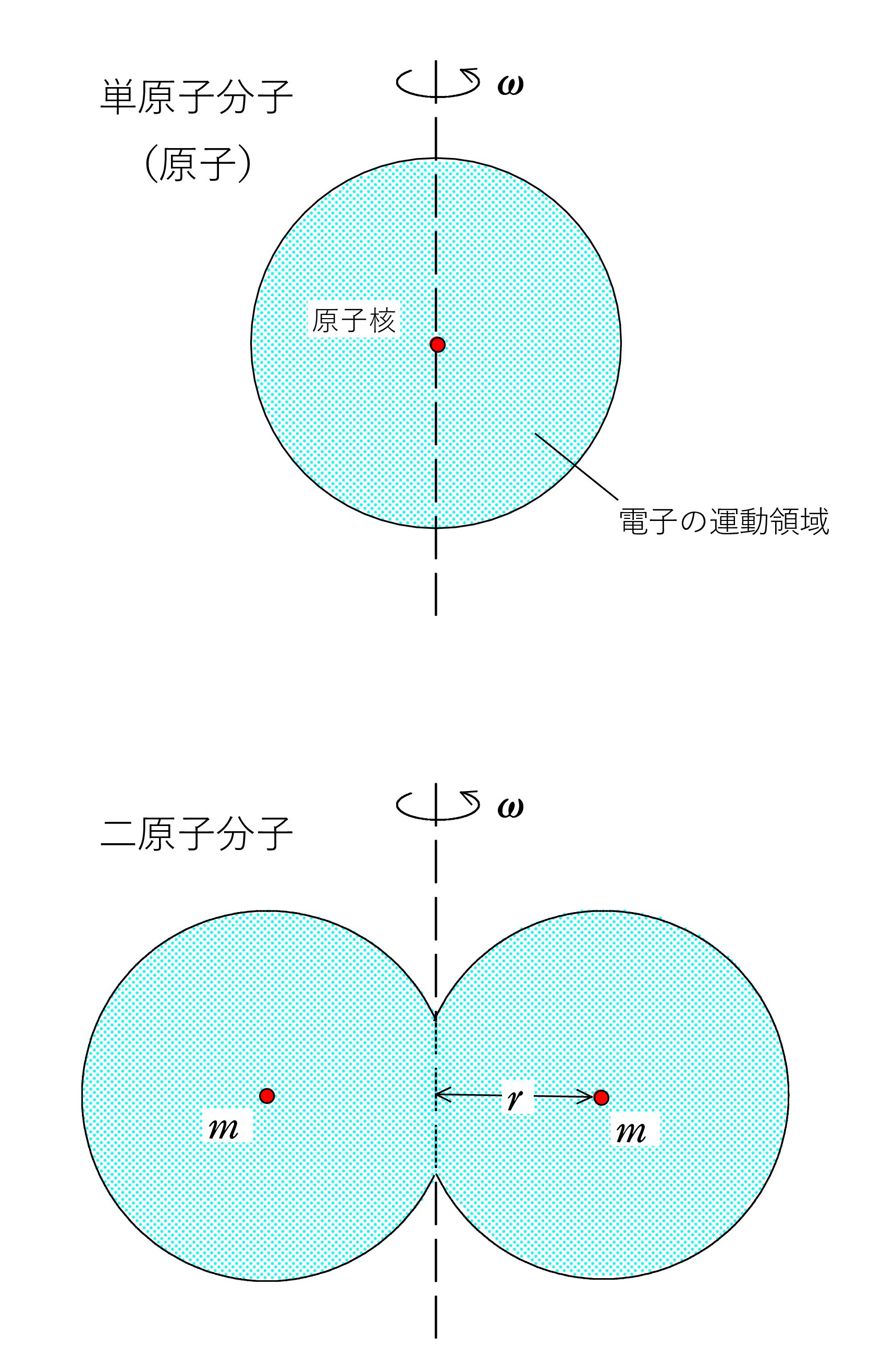A.　きちんとした理解は高校の範囲をはるかに超えてしまうので、今は以下のように考えればよいでしょう。
　その前に、知識の確認ですが、原子は原子核とその周りを回るいくつかの電子からできています。
電子は軽いので、原子の質量は事実上、原子核の質量 です。そして、原子核は大変小さく、原子の大きさの10000分の１に達しないぐらいです。

　さて、回転の角速度を ω とします。
　二原子分子の場合、回転の速さ ｖ ＝ ｒ ω より　２つの原子の運動エネルギーは　　２ × ｍｖ²/２ ＝ ｍ ｒ² ω²　
　一方、単原子では　ｒ ≒ ０　ですから、０とみなせるのです。 あえて言えば、原子核の自転のエネルギーがありますが、原子核の半径が小さいので、無視できます。

　以上、簡単のために、二原子分子を構成する原子を同じとしましたが、異なる原子でも構いません。ただ、回転は重心が中心になります。重心は原子核を結ぶ線分を質量の逆比で内分した点ですね。




Q2.　二原子分子の内部エネルギーは Ｕ ＝ 5/2・ｎＲＴ とのことでした。　覚える必要はありますか ？
　それと、三原子、四原子・・と原子数によって表式が変わっていくのでしょうか。
　

A.　覚える必要はないと思います。ただ、記載している教科書もありますので、入試直前に確認しておくのが安全かもしれません。

　理想気体の内部エネルギーは、一般に，Ｕ ＝ αｎＲＴ と表されます。　単原子分子なら α ＝ 3/2 、二原子分子なら α ＝ 5/2 です。　三原子分子以上は、知る必要はありませんが、α ＝ ３ です。
　回転を考えた二原子分子でも、原子核を結ぶ直線を回転軸とする回転は無視します。単原子の自転と同じように、質量が回転軸上にしかないからですね。
　これに対し、三原子以上ではあらゆる方向での回転が運動エネルギーにつながるために α が３に増えています。　ただし、原子が直線上に並ぶ特別な場合は、二原子分子と同じで、α ＝ 5/2 になるのも理解できるでしょう。



Q3.　内部エネルギーを決める α が 3/2、5/2、7/2 なら数列として分かりますが、
　 　 3/2、5/2、３ は釈然としませんが・・・


A.　自由度という概念で説明されています。
　分子の運動は、重心の運動 と 重心を中心とする回転運動 に分けられます。
　重心運動は ｘ、ｙ、ｚ の３方向で独立に扱えます。　自由に動ける方向が３つなので、自由度が３あるといいます。
　一方、回転運動は、ｘ 軸、ｙ 軸、ｚ 軸 をそれぞれ回転軸とする独立な３種の回転運動として扱えます。ここにも自由度が３あります。

　単原子分子は 回転運動がないので、持てる自由度は重心運動による３です。
　二原子分子は 原子を結ぶ直線（ｘ 軸 とします）を軸としての回転が寄与しないので、　重心運動の自由度３に、y 軸と z 軸回りの回転の２つが加わり、自由度は合計５です。　　先ほどの図では、点線が ｙ 軸で、ｙ 軸回りの回転を示しています。ｚ 軸はこちら向きになっていて、画面内での回転が対応します。
　三原子分子以上は 重心運動と回転運動のすべてができるので、自由度は６あります。

　自由度１つ分について、運動エネルギーが 1/2・ｎＲＴ であることが知られていて、内部エネルギーが決まります。
　ただし、三原子分子以上では、振動運動も寄与し始め、α＝３ からずれる例が多くなります。　今はこれぐらいにしましょう。すでに入試の範囲を逸脱しています。
　





Q.　教科書では、単原子分子と二原子分子の違いを、定積モル比熱 Ｃ_V や 定圧モル比熱 Ｃ_P の実験結果で比較しています。 内部エネルギーで比較することと同等でしょうか ？


A.　同等です。実験としてはモル比熱が測りやすいので、そうしています。
　理論上は、内部エネルギーからモル比熱を導出します。

　Ｕ ＝ αｎＲＴ から出発しましょう。　Ｕ と Ｔ が比例しているので、�凾t ＝ αｎＲ�凾s となり、重要公式 �凾t ＝ ｎ Ｃ_V �凾s と見比べれば、 Ｃ_V ＝ αＲ であることが分かります。　Ｕ ＝ ｎ Ｃ_V Ｔ を知っていれば、もっと話が早いです。　式として知らなくても、　内部エネルギーは絶対温度で決まる（圧力や体積には関係しない）ことは大変重要 です。
　さらに、 Ｃ_P ＝ Ｃ_V ＋Ｒ　の関係があるので、 Ｃ_P ＝（α＋１)Ｒ になります。 　α が決まれば、 Ｃ_V 、 Ｃ_P が決まるのです。　α ＝ 3/2 が単原子、α ＝ 5/2 が二原子分子です。
　単原子の Ｃ_V ＝3/2・R 、 Ｃ_P ＝5/2・R は覚えておいてください。

　念のためですが、�凾t＝ｎ Ｃ_V �凾s が重要と言ったのは、定積変化に限らず、任意の変化で成り立つ からです。
単原子という条件がなく、 Ｃ_V が与えられているケースでは、熱力学第１法則の �凾t として用いられます。
　一方、熱量 Ｑ ＝ ｎ Ｃ_V �凾s は定積変化に限られます。 混同のないように。

　











波 動　　//////////////////////////////////////////////////////////////////////////////////////////////



Q.　２つの波源 A 、B 間にできる定常波についての質問です。２つが同位相のときは中点が腹になり、逆位相のときは節になるのは分かります。あとは、腹と腹（節と節）の間隔が半波長 λ/2 であることから定常波の全体像がつかめます。　ですが、たとえば、B の位相が π/2 遅れているときはどう扱えばいいんですか。　　（π：パイ、円周率）
　

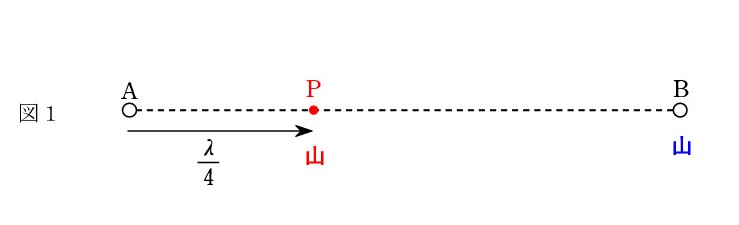
A.　位相２π が波長 λ に対応するので、π/2 は λ/4 に対応します。A から出た山が λ/4 進んで点 P に達した時、B が山を出します。２つの山が出会うのは P B の中点です。そこが腹ですね（図1）。あとは λ/2 の間隔で追えばいいでしょう。　なお、B は T/4 遅れて振動しています（T：周期）。

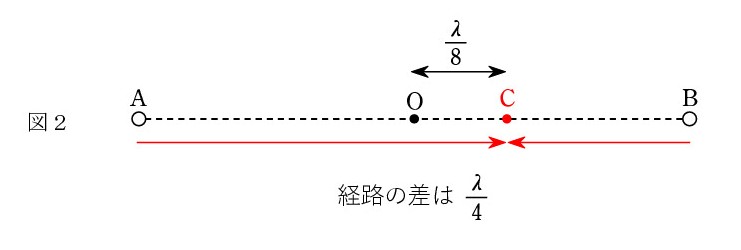
　中点 O を利用して考えるのがスマートです。 λ/4 のハンディキャップがあるので、中点より B に近い側の点 C で山と山が出会うはずです。距離 O C はいくらですか ？・・・　　 λ/4 ？ ・・・ O C = λ/8 ですね（図2）。　A から遠ざかり、B に近づくので経路差は O C の２倍です（要注意！）。

　B の位相の遅れが φ なら、(φ/2π)λ のハンディなので、中点 O の右、φλ/4π の位置が腹ですね。　具体例で考えて一般化するのは、物事を考える上での鉄則 です。　次に、式ができたら、答えが分かっている例でのチェックが大切。この場合は、φ ＝ ０（同位相）や　φ ＝ π（逆位相）です。

　位相の違いを距離に置き換えて考えてきましたが、時間の違い（φ/2π）T に置き換え、時間に着目して考えることもでき、いろいろな方法があるとだけ言っておきます。







Q.　斜め方向のドップラー効果では、音源と観測者を結ぶ「直線」が重要で、その方向の速度成分を取り出して考える必要がある ことは知っています。　しかし、いつの時点で音源と人を結ぶのでしょうか ？　　音源が動く図１の場合、Ｂ点にいる人に音が届いたとき、音源はすでにＡ点にはいないはずですが・・・大丈夫ですか ？

　
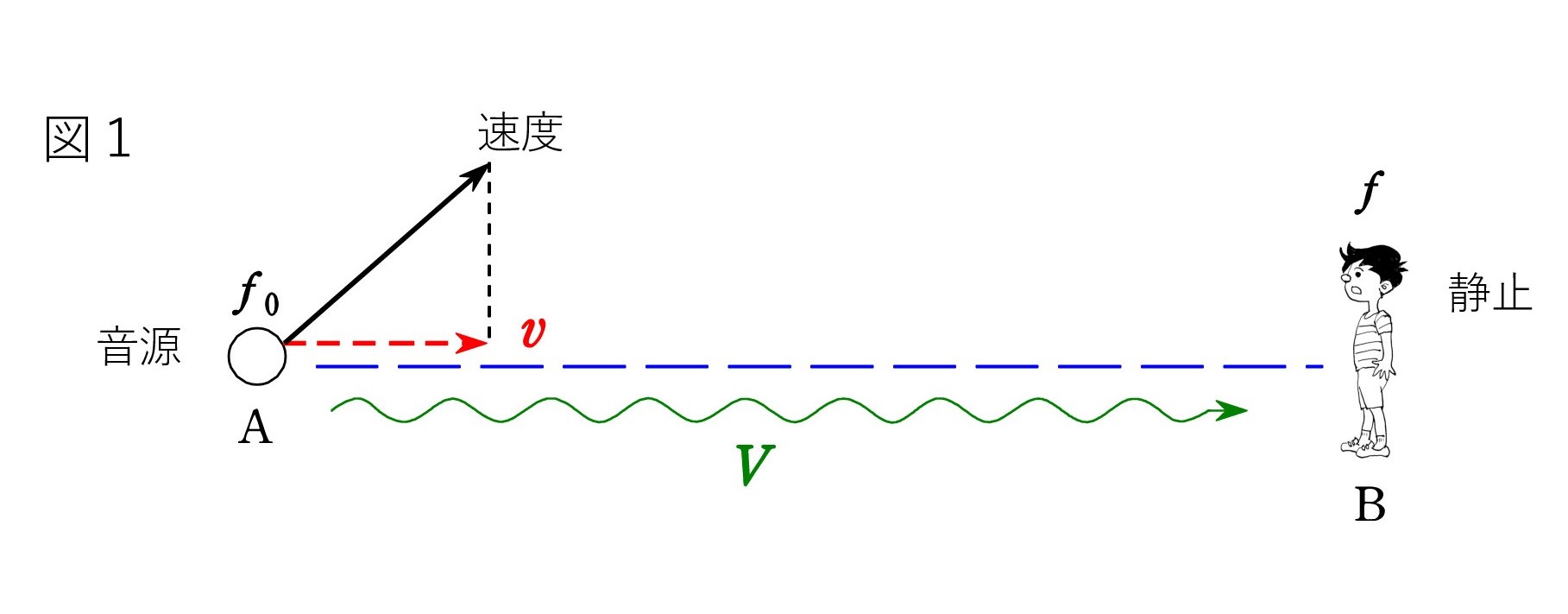
A.　「直線」は音波が伝わった経路のことです。Ａ点で出された音が人に届いたとき、どのように聞こえるかを問題にしています。人が音を受け取った時、音源がどこにいるかはどうでもよいのです。Ａ点での速度成分ｖが大切で、音源の振動数を ｆ₀ とすると、人が聞く振動数 ｆ は　ｆ ＝ ｆ₀・Ｖ/（Ｖ−ｖ）ですね。　（Ｖ：音速）

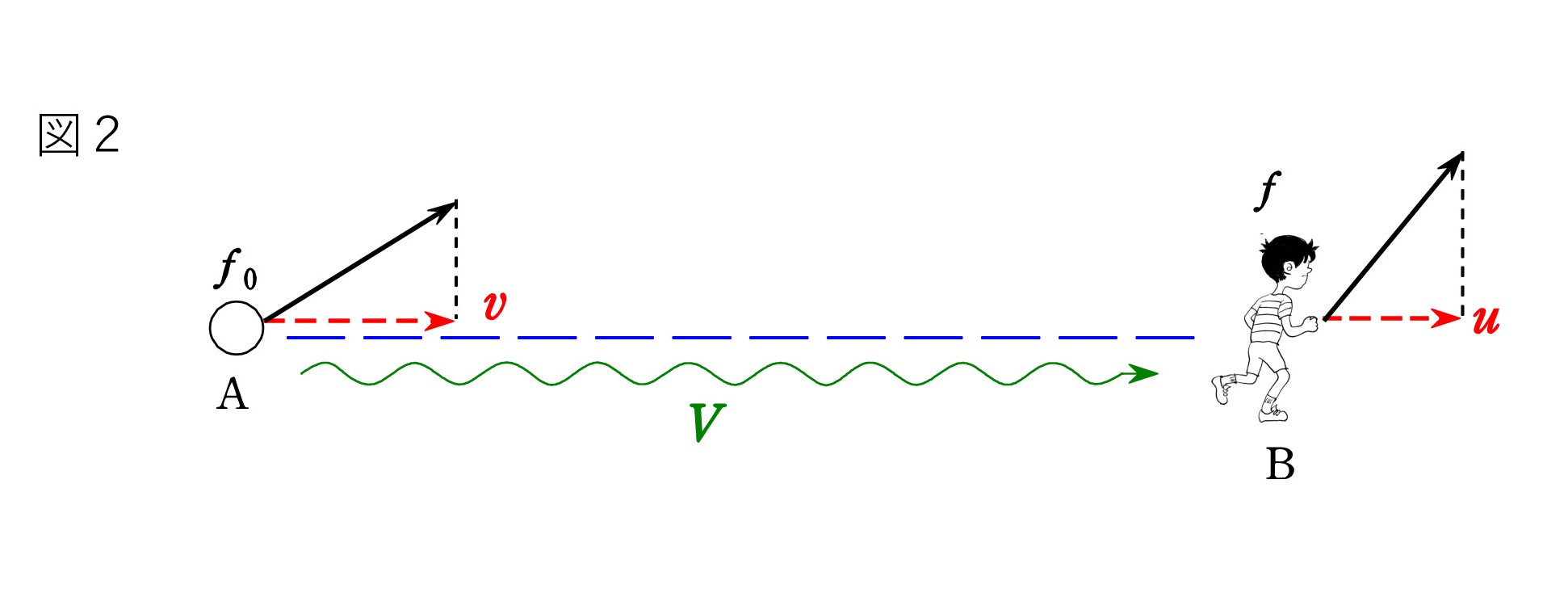
　図２は両者が動くケースですが、Ａ点で音が出された時の速度成分 ｖ と、Ｂ点で人が受け取った時の速度成分 ｕ が大切です。　この場合は、公式通り、
　ｆ ＝ ｆ₀（Ｖ−ｕ）/（Ｖ−ｖ） です。　ついでながら、音波が伝わる向き（図では右向き）を正とすれば、 u と v は符号つきで OK ということは知っていますよね。

　音源と人が同時に「直線」上にいるわけではなく、ていねいに言えば、Ｂ点で人が音を聞いたとき、その音が発せられた点Ａを定め、音源がかつてＡ点を通った時の速度を確かめ、ＡＢ 方向の成分 ｖ を調べ、同じく聞いた時の ｕ を調べるということです。

　ＡからＢへ向かう音波の波長が ｖ で決まります。音速 Ｖ で伝わり、人の ｕ で観測振動数 ｆ が確定するという次第です。
　音速 Ｖ は一定で、 音源の速度の影響を受けない というのはドップラー効果の基本中の基本ですね。






Q1.　点音源が速さ ｖ で動くとき、斜め方向でのドップラー効果は、音源と観測者を結ぶ直線方向の速度成分 v cos θ を用いて振動数の公式を適用すればよいことは知っています。　しかし、山の波面を描いた図を見て下さい。波面の間隔が波長です。　前方と後方へ向かう波の波長はそれぞれに一定ですが、角度 θ 方向では一定になっていません！
　波長が決められなければ、振動数も決められないと思いますが・・・？

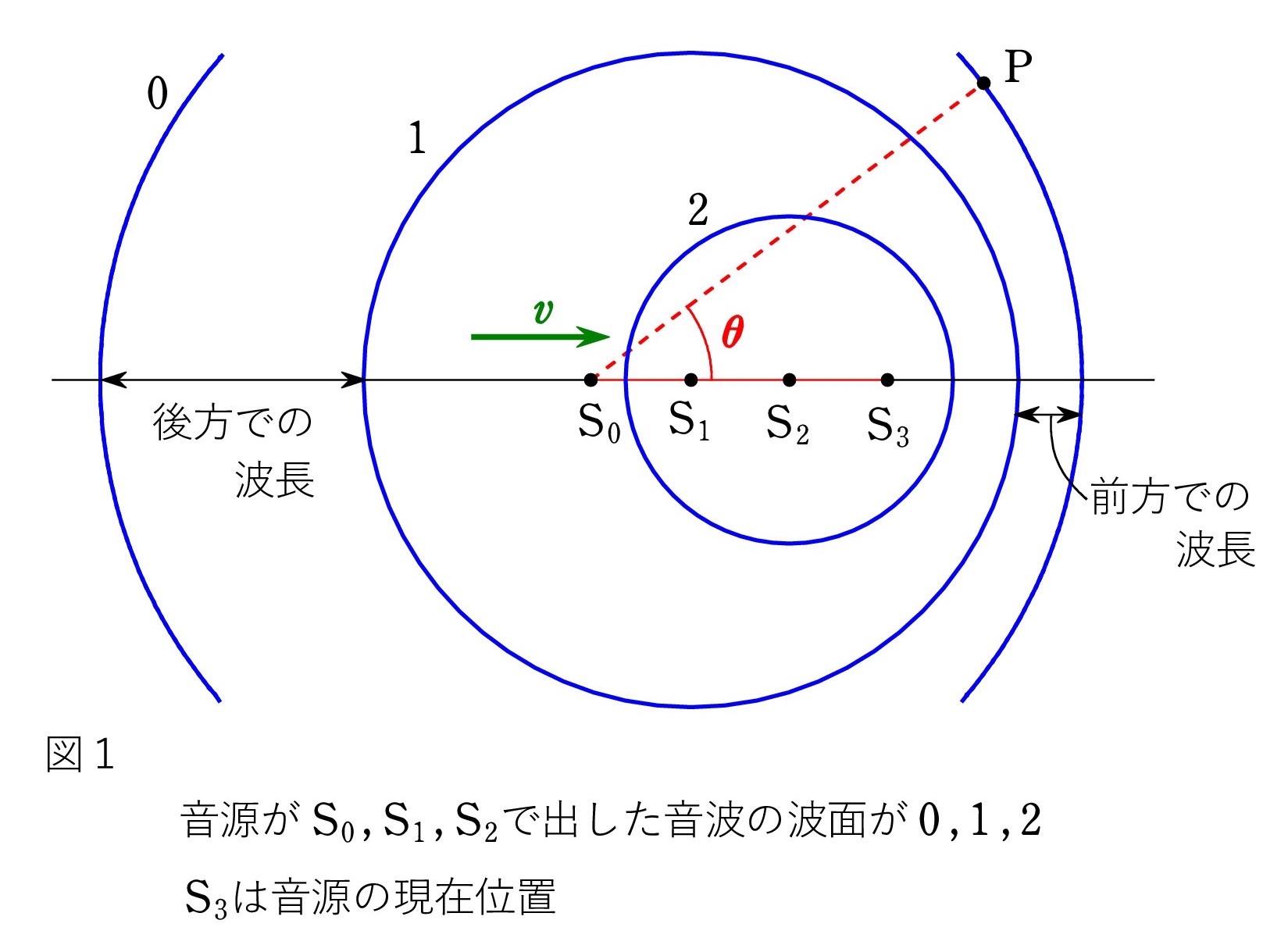
A.　　音速は 音源の速度によらず 一定 なので、どの波面も出された点を中心として球面波として広がっています。　音源が動き、音波の発生位置が移動するため、前方に向かう波の波長は短くなり、後方に向かう波の波長は長くなる のが端的に分かる図です。　ドップラー効果では最も重要な図と言っていいでしょう。　しかし、質問の通り、斜め方向では 波長が 見た目におかしくなっていますね。

　実は、斜め方向のドップラー効果では「波長が短い」という条件が必要なのです。
　図２では 波長を短くしてみました。これだと、θ 方向でも 波面の間隔は一定に近いのが分かるでしょう。　点Ｐで観測する S₀ からの音が続くのは ほんの短時間のことなので、点Ｐ近くの波面に注目しています。

　ていねいに言うと、観測者が点 P にいるとき、S₀ P 間距離ｄに比べて波長が十分短ければよいのです。　式にすると、ｄ ≫ λ₀　です。　λ₀ は音源が静止しているときの波長で、音源の振動数をｆ₀ とすると、音速 Ｖ ＝ f₀ λ₀
　この条件を満たせば、近似的に ｆ ＝ f₀・V / (V−ｖｃｏｓθ)　が成立します。　詳細は「名問の森」(上) の問題 70 で扱っています。 そこでは　ｄ ≫ ｖ/ｆ₀ となっていますが、ｄ ≫ λ₀ であれば十分です。　それは、 Ｖ ＞ ｖ であり、　ｄ ≫ λ₀ ＝Ｖ/ｆ₀ ＞ ｖ/ｆ₀　から分かります。　ｄ ≫ λ₀ なら 近似の意味が 上図のように 直感的に理解 できます。

　今、点Ｐで観測しようとしている音波は、音源が S₀ の位置で出したものですが、音源は S₃ にいることにも注意してください。　θ を測るときに必要な認識です。

　現実的には、斜め方向のドップラー効果は飛行機や列車などのケースで出題され、ｄ が大きいことで条件が満たされています。　図２を拡大して図１の波長にしてみたときを想像してほしいのですが、ｄが大きくなれば、大丈夫です。



Q2.　ｄ ≫ λ₀　であれば よいのは分かりました。「森」の問題70 では、ドップラー効果の公式に頼らず、かなり長い計算をし、近似を経て、 ｆ ＝ f₀・V / (V−ｖ cos θ)　に達しています。　公式に頼らないと、簡単には得られない式ということでしょうか。


A.　　問題70 では 音の継続時間(周期)に注目して導いていますが、 波長で考えると早い です。　ドップラー効果の公式の導出 にもつながる話です。

　まず、慣れるために、前方に向かう音波から始めましょう。
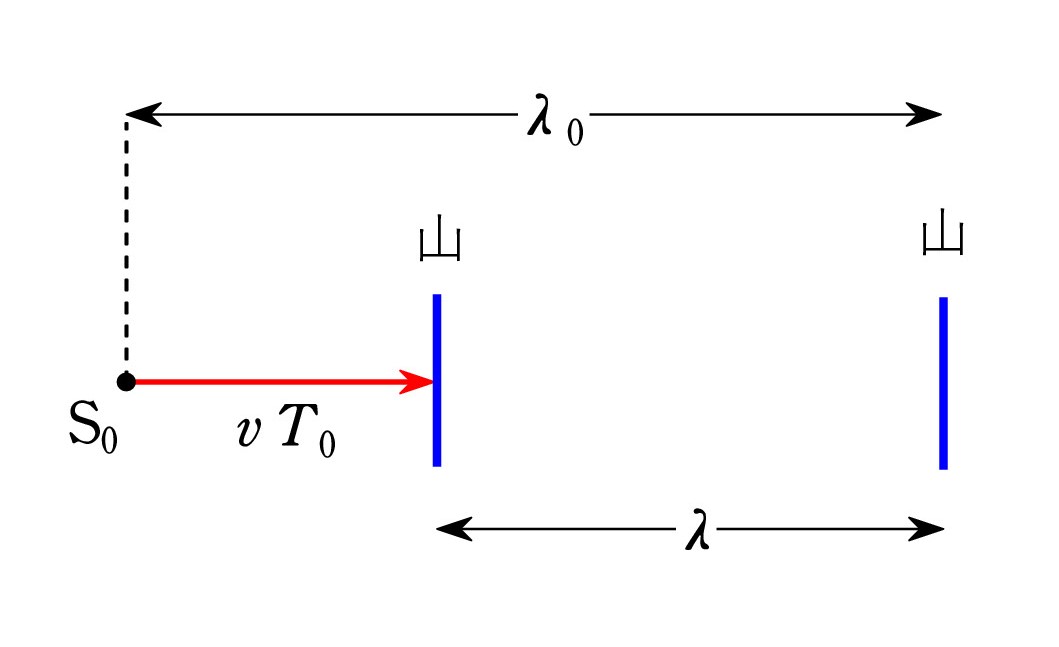　音源が S₀ で山を出すと、その波面は１周期 T₀ の間に λ₀ だけ進みます。　音速Ｖで進むので　VT₀ ＝ V/ f₀ ＝ λ₀ と考えてもいいです。
　音源が静止していれば、 S₀ の位置で次の山が生じ、波長は λ₀ になりますが、いまは速さｖで動いているので、ｖT₀ 右に移動した位置で 次の山が生じ、山と山の間隔、つまり、波長 λ は　λ ＝ λ₀ − ｖT₀　になります。
　Ｖ＝ f₀ λ₀　と　Ｖ＝ｆλ　それに　T₀ ＝ １/ f₀　の関係を用いると、
　　　　　　　　　V/ f ＝ V/ f₀ − v/ f₀
　整理すると、　　ｆ＝ f₀・Ｖ/(V−ｖ)　　　まさに公式の形ですね。

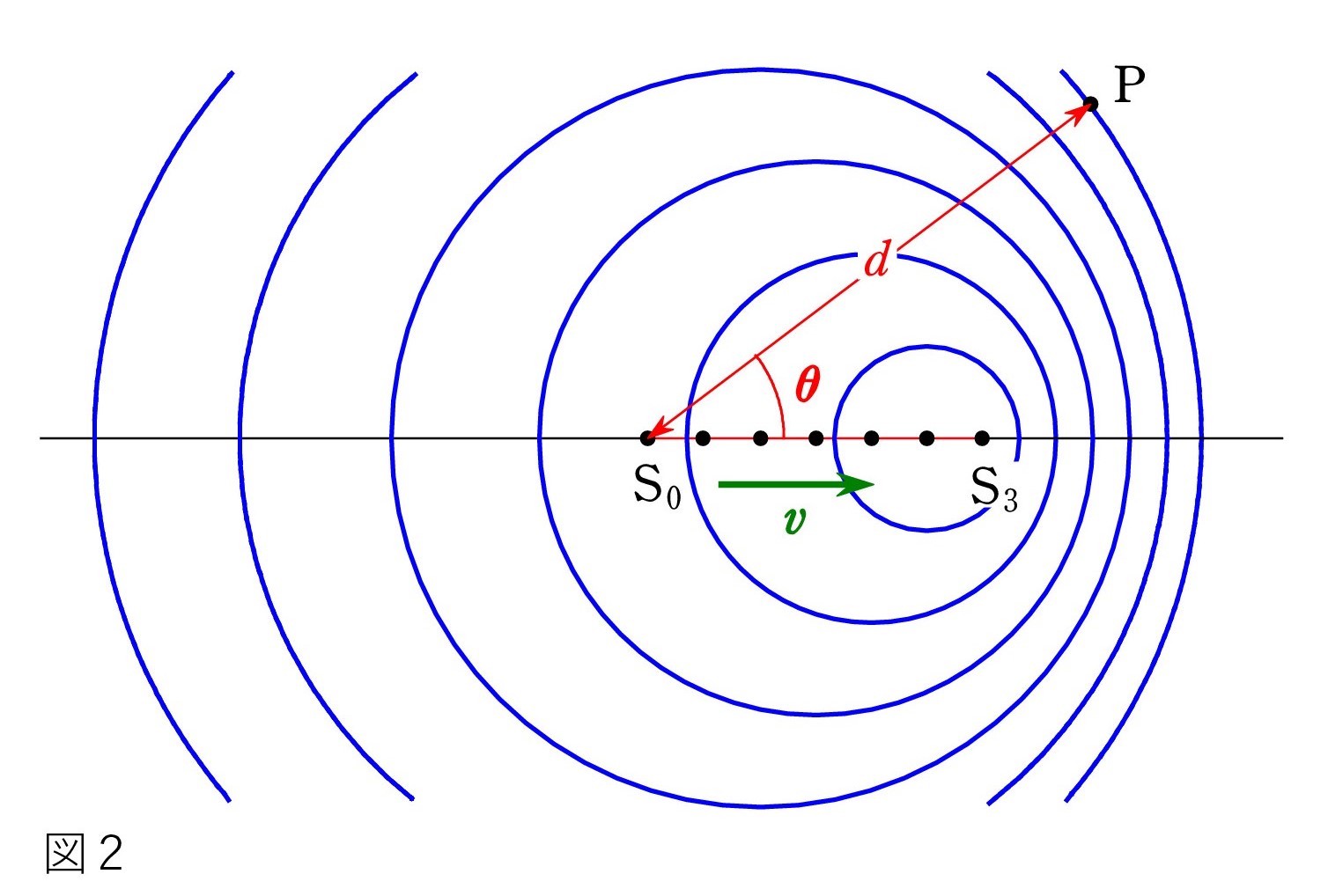
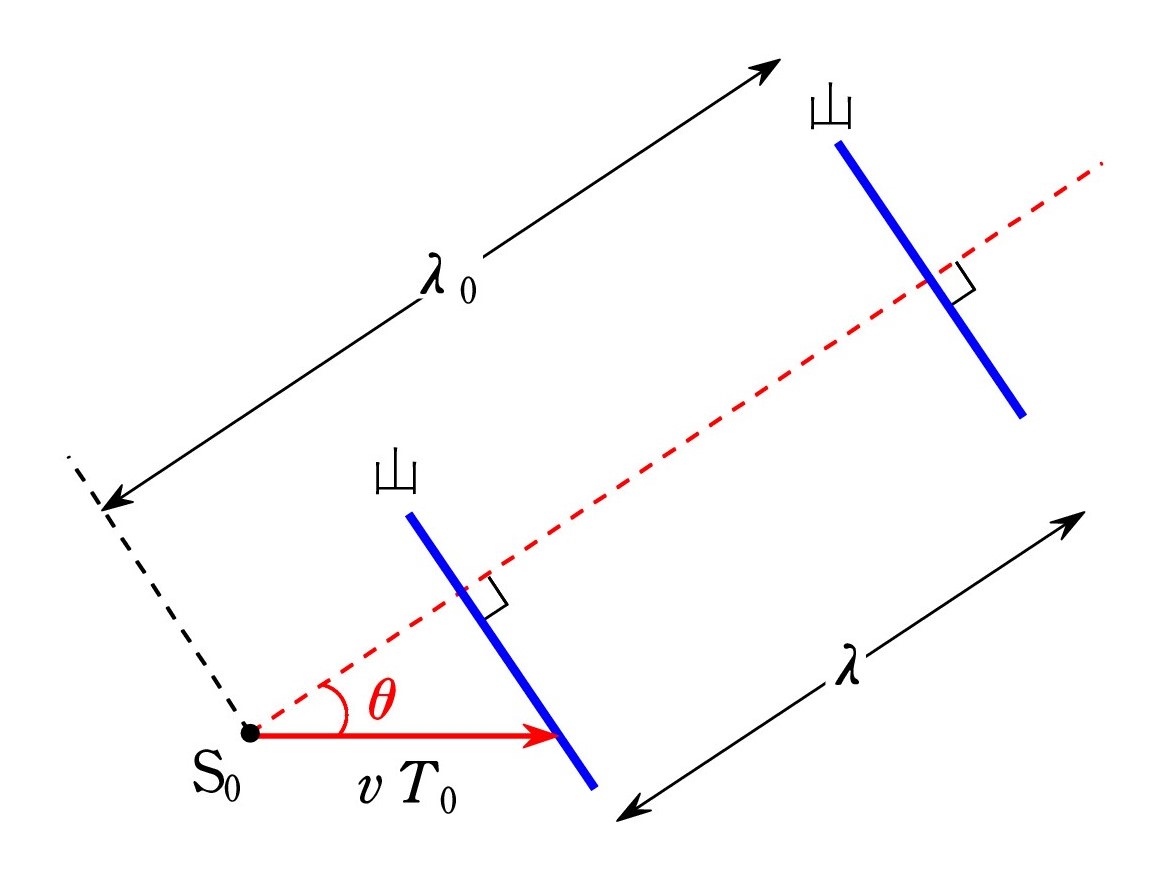　さて、斜め θ 方向です。
　上の図２の点Ｐ近くでは平面波と見なせます。そこで、音源が平面波を出しているとして考えたのが右の図です。　 波面と射線は 直交する ことも意識してください。
図から、　　　λ ＝ λ₀ − ｖT₀ cos θ
先ほどと同様に 振動数に直せば、
　　　 　　　ｆ ＝ f₀・V / (V−ｖ cos θ)　　

　θ 方向に垂直な速度成分はドップラー効果に影響しない という大切な知識も、平面波としてとらえると、波面を変えない（波面を波面方向にずらしても同じ波面である）ことから理解でき、知識が裏打ちされたものになるでしょう。

　問題70 の扱い方は、計算が大変ですが、近似の条件　ｄ ≫ ｖ/ f₀　が明確になる というメリットがあります。　 f₀ ＝ Ｖ/ λ₀　から、この条件は　ｄ ≫ (ｖ/ Ｖ) λ₀　と表せ、　ｄ ≫ λ₀　より少し緩く（満たしやすく）なっていることが分かります。






Q.　高校生を教えています。　いくつかの教科書は「全反射は、入射角が臨界角を超えると起こる」となっていますが、「全反射は臨界角から始まる」としている教科書もあります。　どちらが正しいのでしょうか。
　ちなみに、前者(Ａ)は 数研出版、啓林館、東京書籍、実教出版で、後者(Ｂ)は 第一学習社です。



A.　まず、質問させてください。
　　　「光が境界面に臨界角 θ₀ で入射すると、その後 どの方向に進みますか？」

　　　　・・・・・・・・？・・・？・・・？・・・？・・・？・・・・・・・・



　「屈折角が 90° だから、境界面に沿って進む」という答えによく出会います。　また、もう少し注意深い人は「境界面に沿って進む光と、反射される光に分岐する」と答えます。　いずれにしろ、前者Ａの記述が正しく、後者Ｂは誤りということになりそうです。

　ところが、最も現実に即した答えは「反射角 θ₀ で反射される」だと思います。　後者Ｂとも少し異なり、「全反射は、事実上、臨界角から始まる」という認識(Ｂ’)に基づいています。　事情については、拙著「物理 授業の実況中継」(語学春秋社) に記していますので、次に引用しておきます。

• 「実況中継」からの引用

　当然ながら、問題に対する解答に違いが生じます。たとえば、全反射するための入射角 θの条件を尋ねられれば、Ａなら、θ ＞ θ₀ ですし、それが多数派です。　一方、Ｂ や Ｂ’ なら、θ ≧ θ₀ です。　等号のあるなしは、生徒にとっては大問題です。　光ファイバーの問題ではそれが何設問も続き、気にならないわけがありません。
　「数学と違って、物理は境界のところは問題にしないから、どちらでもよい」と一般論を持ち出して済ますこともできますが、臨界角のとき何が起こっているのかという認識は大切です。

　私自身は、出版物では　θ ＞ θ₀ として解答を書いています。　本当は　θ ≧ θ₀ としたいのですが、Ａの教科書に従う多数派の人からクレームが来ることは目に見えています。　　そこで、　θ ＞ θ₀ とした後には「等号を付けてもよい」と断り書きを入れています。
　生徒にも、入試では出題者の意向がはっきりしていればそれに合わせ、不明のときは多数派に合わせておくのが安全と伝えています。　風見鶏のようですが・・・









Q1.　レンズの公式　1/a ＋ 1/b ＝ 1/f　において、ａ が負となるケースについて「エッセンス」では次のように書かれています。

　図２もコピーします。　逆行を考えれば、「虚像」の位置に向かおうとする光が、「物体」の位置に実像を結ぶのは分かります。　でも、なぜ ａ を負とすればよいのか、理由を知りたいです。

　

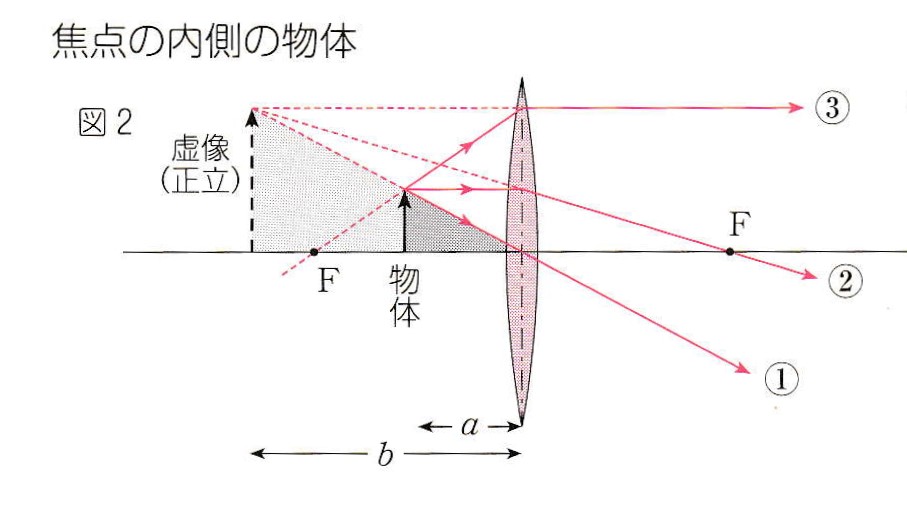
A.　図２のＦは焦点で、焦点距離がｆです。　a、b は距離であり、正の値です。　まず、図２のままでレンズの公式を用いると、虚像なので、　1/a ＋ 1/(-b) ＝ 1/f　（式 A） ですね。

　では、逆行のケースです。　波は逆行可能 なので、�@、�A、�Bの光線を逆向きにしても成り立ちます。　右からレンズに向かう３つの光線は点線矢印の先端を目指しています。　そしてレンズで進路を曲げられ、実線矢印の先端で出合います。　実像を作るのです。

　レンズがなければ一点に集まる光を後方の光源と表記しましたが、「虚物体」とも呼ばれます。
　逆行の場合、図２の「虚像」を「虚物体」とし、「物体」を「実像」と読み替えてください。　虚物体までの距離がｂで、実像までの距離がａです。
　逆行させても、上の式 A の関係は変わらないはずです。　そこで、左辺の項を入れ替えると、　　　　1/(-b) ＋ 1/a ＝ 1/f
　これをレンズの公式に該当させると、第１項は物体に対応し、第２項は像に対応します。　虚物体の場合は負にすればよいということです。




Q2.　凹レンズの 図３の場合はどうでしょうか。

　

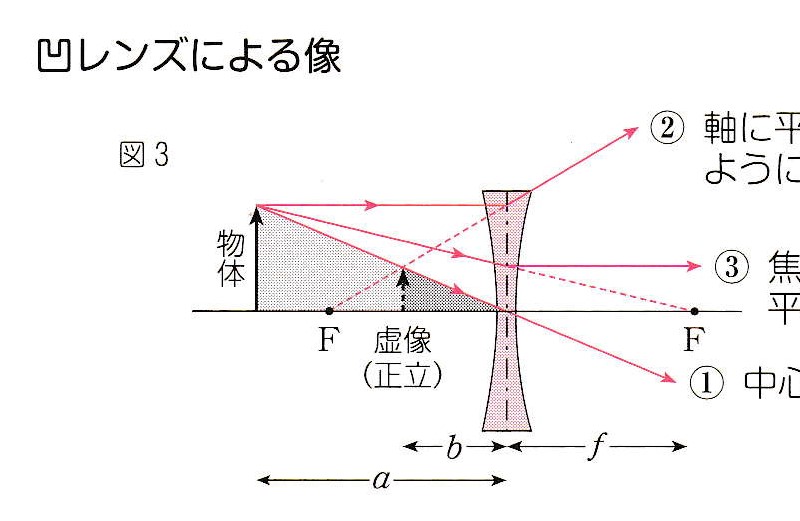
A.　まず、図３に対して、　　　1/a ＋ 1/(-b) ＝ 1/(-f)　（式 B）
　凹レンズなので、焦点距離を負にしています。 また、虚像なので左辺の第２項が負です。

　次に、逆行させると、「虚像」が「虚物体」になり、「物体」が「実像」になります。　それは式 B の左辺の項を入れ替えた　 1/(-b) ＋ 1/a ＝ 1/(-f)　に他なりません。




Q3.　「逆行」は意外なことを教えてくれますね。　少し感動しました。
　a が負になる「虚物体」も分かりました。　反射鏡でも起こるのでしょうか。


A.　　反射鏡の場合もレンズの公式が成り立つことは知っていますね。　注意点は、凹面鏡が 凸レンズに対応することです。　共に光を集め、光軸に平行な光線は一点(焦点)に集まります。　公式が成り立つことは相似三角形を利用して確認でき、教科書に書いてあります。　焦点距離 f は 凹面鏡が正で、像までの距離 b は 実像が正です。

　凸レンズを通した後、実像を結ぶ前に反射鏡を置くと(初めの図の点線位置)、「虚物体」になりますが、やはり a を負にすることで対処できます。
　教科書の図で 虚像ができる場合に、光を逆行させてみてください。　虚像は「虚物体」に、物体は「実像」に変わり、あとはレンズの公式の 左辺の第１項と第２項を入れ替えて 見比べてみると分かります。

　ただ、反射鏡はレンズに比べると出題率が低く、ましてや「虚物体」が入試で扱われた例はないと思います。　逆行の有用性だけ 味わってください。








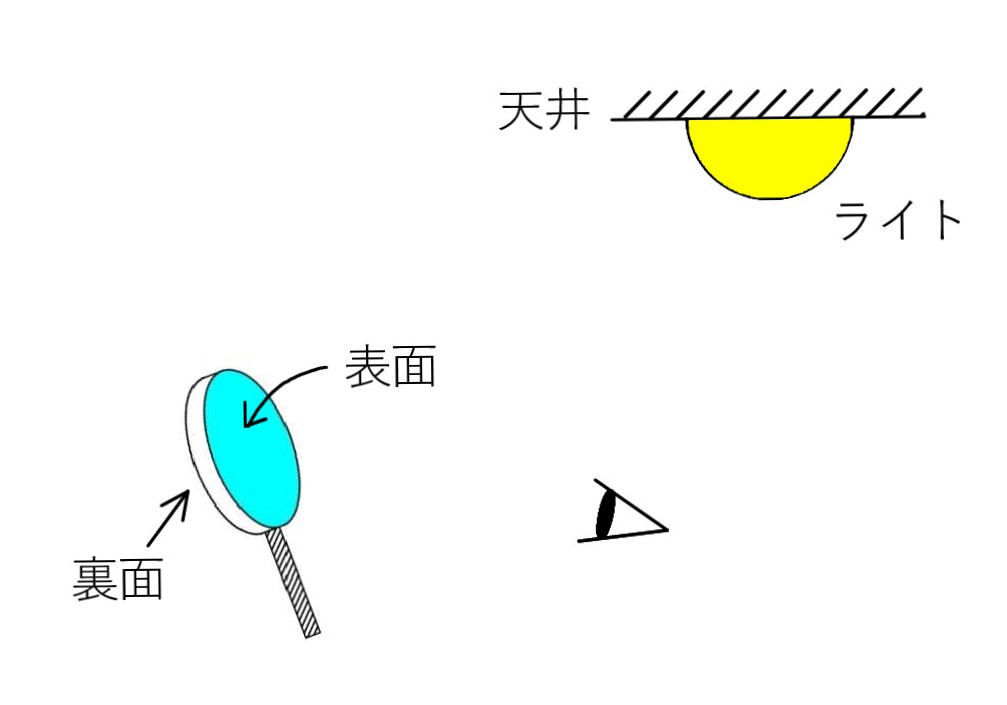Q1.　「凸レンズによる実像をスクリーンなしで見られるか？」という話を『Q＆A 風』で読み、虫眼鏡で確認しました。　その後、何気なく虫眼鏡を見ていたら、後方の天井のライトが映っていました。　よく見ると、なんと、２つの像が映っていたのです！
　１つはレンズ表面での反射によるものと思いますが、もう一つは何でしょうか？
　なお、虫眼鏡の向こう側(裏面側)に黒い紙を置いても、２つ見えることに変わりはないです。　レンズを通り抜けた光は関係ないようです。


A.　　確かに、１つはレンズ表面での反射像です。ていねいには、虚像で正立です(像 X)。　窓ガラスによる反射と本質的に同じものですね。

　さて、もう一つですが、レンズの裏面による反射です(像 Y)。　２つの像のうち小さい方です。レンズに入った光が裏面で屈折して出ていくとき、同時に反射が起こります。このとき、裏面は凹面なので、凹面鏡となって、反射像を作ります。

　教科書で凹面鏡の反射、それも物体が焦点の外にある場合を見て下さい。ライトは遠いので、このケースが該当します。　像は実像で、虫眼鏡から浮き上がって手前に見えているはずです。そして、倒立しているはずです。




Q2.　像 X の正立と Y の倒立は確認できました。　ライトの形が丸なので、端を覆って非対称にしたらはっきりしました。　倒立とは、180° 回転した像ですね。
　そして、X はレンズの向こう側に、Y は手前側にできているということですね。なんとなくそんな気もしますが・・・

A.　　虫眼鏡の取っ手を軸にしてほんの少し回してみると、遠い X と近くの Y の位置関係が分かります。　ゆっくり回したり戻したりしてみてください。線分 XY がレンズ面と交わる点を中心にして向きを変えます。
　また、スリガラスかトレーシングペーパーがあれば、実像 Y を映し出せます。　クッキリ映る位置があるはずです。入射光を遮らないようにしてください。




Q3.　裏面を凹面鏡と捉えるのが面白いですね。ガラスから空気へ光が向かうので、鏡とは思えませんでした。屈折と反射は「２つの媒質の境界面で同時に起こる」ということですね。　ただ、光の反射は弱く、暗くて見えないということはないのでしょうか。


A.　　私も初めて話を聞いた時にはそう思いました。実際にやってみると、意外によく見えます。　凹面鏡になっている裏面で光が集められることで明るくなっています。
また、像 X に比べて Y は小さくなっていますが、それは明るくなることにつながります。　教科書の凹面鏡による反射の図でも小さくなることが確認できます。

　裏面で反射された光は、次にレンズの表面で屈折して出てきます。このとき、表面はまさに凸レンズとして集光し、さらに像を明るくしています。

　











電磁気　　//////////////////////////////////////////////////////////////////////////////////////////////



Q.　万有引力の法則 GMｍ / r² と クーロンの法則 ｋQq / r² とは同じような形をしていますね。　質量と電気量が対応し、何より距離ｒの２乗に反比例している点が同じです。
　固定された正の点電荷 Q の周りを等速円運動する負の点電荷 −ｑ の問題に出会い、万有引力で天体の周りを回る衛星の話と似ていると思いました。　点電荷の場合にも楕円軌道は可能ですか？


A.　可能です。入試での出題例もあります。　ケプラーの第２法則である「面積速度一定」も成り立ちます。 これと力学的エネルギー保存則　ｍｖ² / 2 ＋ (−ｑ)×ｋQ / r ＝ 一定　を連立させて、楕円の長軸の両端での速さを求めることもできます。　第２項の静電気力による位置エネルギーは、公式 U ＝ ｑV と点電荷の電位の公式 V ＝ ｋQ / r を組み合わせたものです。

　楕円軌道が可能なのは、万有引力の法則とクーロンの法則は同形なので、類推により理解できます。

　静電気力の位置エネルギー −ｋQｑ / ｒ は 万有引力の位置エネルギー −GMｍ / r とそっくりなのも類推で分かりますね（いずれも無限遠点基準）。

　類推（アナロジー）は大切な見方 で、物理に限らず、科学一般で用いられています。








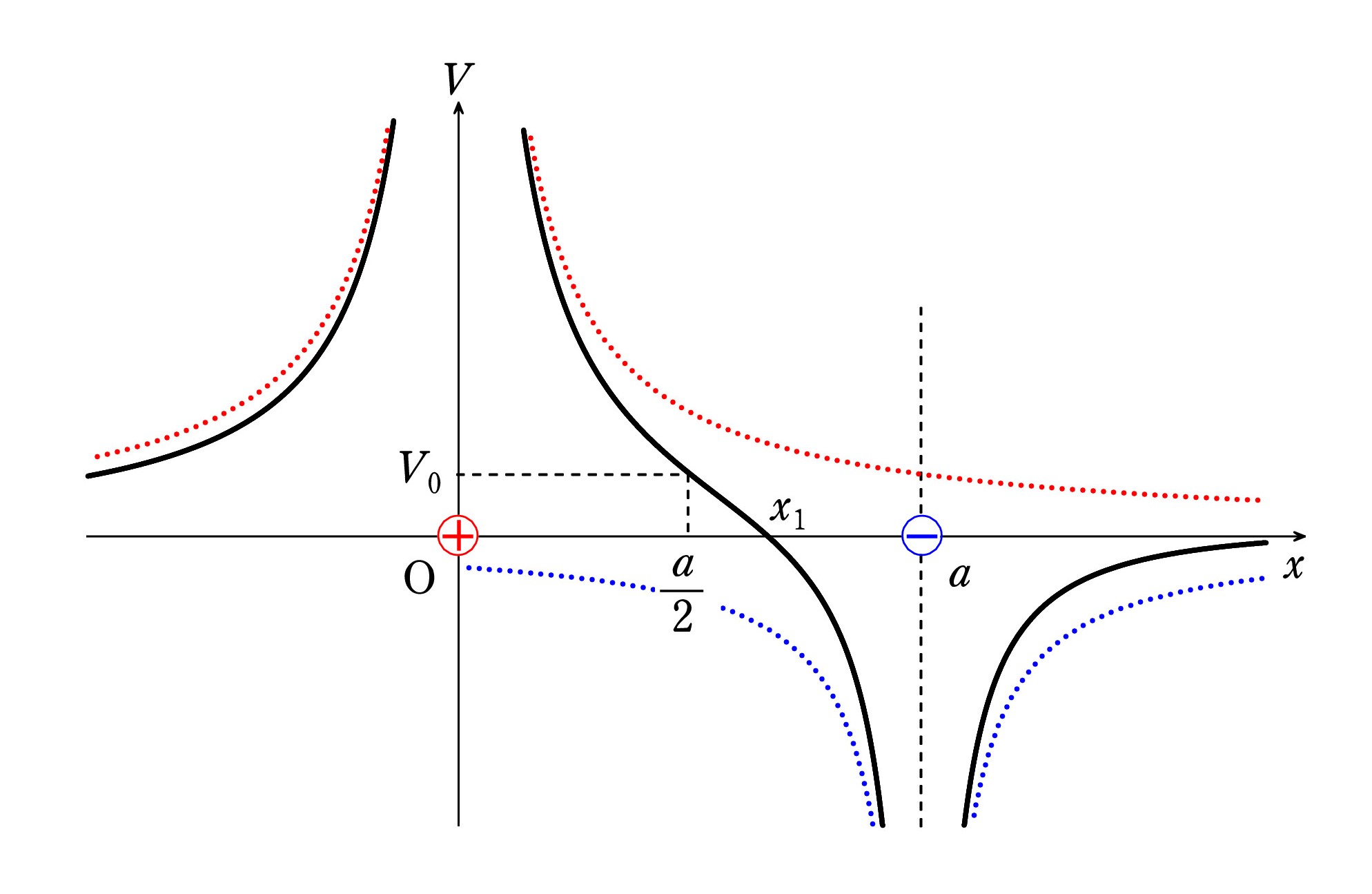
Q.　正と負、２つの点電荷が置かれている場合の電位のグラフを描いたら、試験で減点されました。
　「エッセンス」の電磁気の問題６(新版は８)と同じで、＋2Ｑ と −Ｑ があるときの ｘ 軸上の電位 V のグラフです。　電位の基準点は無限遠点なので、右のように描きました。　点線は各点電荷による電位で、その和が答えになります（実線）。
　正電荷の方が大きいので、中点 ｘ ＝ ａ/２ で Ｖ＞０ となることにも注意したつもりですが・・・。

　なお、グラフは概略でよいとありましたが、中点での電位 Ｖ₀ と、電位が０となるｘ₁ は調べてみました。　公式 Ｖ ＝ ｋＱ/ｒ を用いています。
　　　　　V₀ ＝ ｋ・２Q/(a/2) ＋ ｋ・(−Q)/(a/2) ＝ 2ｋQ/a
　ｘ₁ は、　０ ＝ ｋ・２Q/ｘ₁ ＋ ｋ・(−Q)/(a − ｘ₁)　より　　ｘ₁ ＝ 2ａ/３


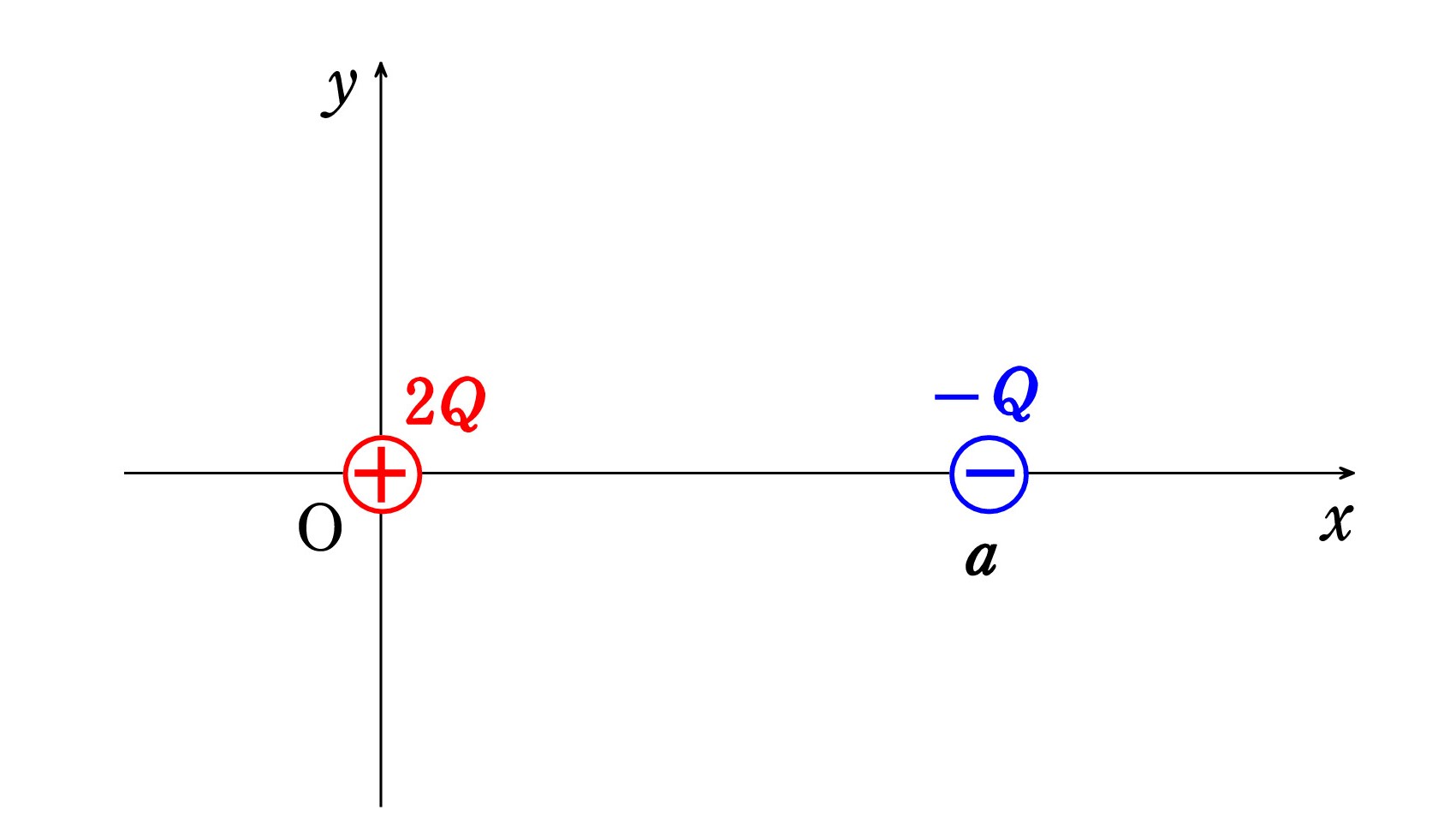
［問題6］ｘｙ平面上、原点Ｏ(０，０)に ＋2 Q、点（a，０）に −Ｑ がある。　電場が０となる点の座標（ｘ₀ ，ｙ₀ ）を求めよ。


　　　　（ 答： ｘ₀ ＝（ 2＋√2)a ，ｙ₀ ＝ ０ ）



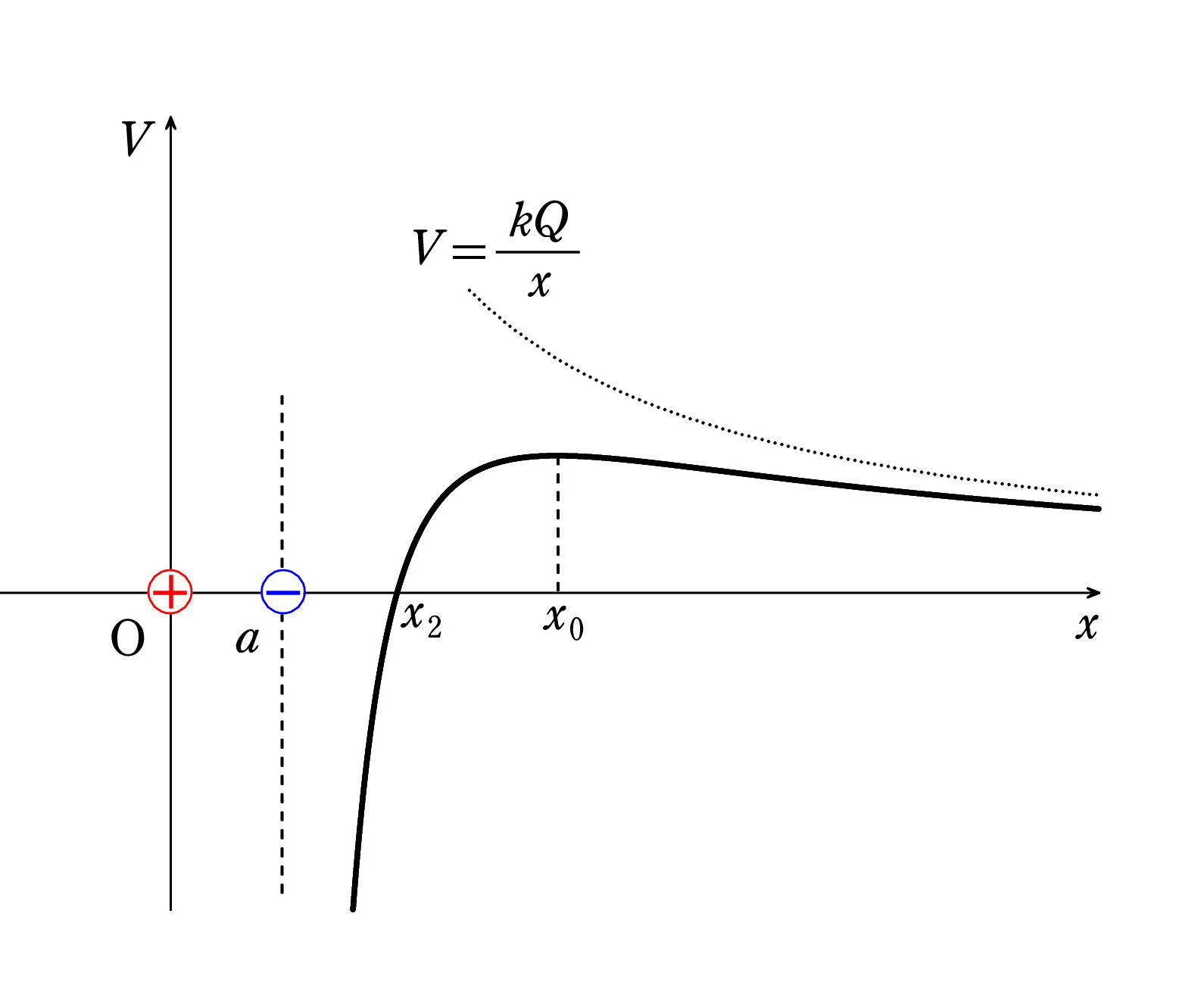A.　ｘ＞ａ の領域での形状で減点されています。
　確かに負電荷の近くでは Ｖ＜０ ですが、離れていくと、Ｖ＞０ になるはずなのです。　２つの点電荷はやがて丸ごと1つの点電荷と見なせる状況になります。 ａ に比べて ｘ がはるかに大きいところです。
　その電荷は、＋２Ｑ ＋（−Ｑ　）＝ ＋Ｑ であり、 正電荷ですから電位 Ｖ は正になりますし、Ｖ ＝ ｋＱ/ｘ が漸近線になると言えます。
　正しいグラフは右のようになります（ ｘ＞ａ の領域だけ示します）。

　電位 Ｖ グラフの接線の傾きが電場 Ｅ を表す ので、問題6で求めた ｘ₀ ＝ (2＋√2)a で傾きが ０、つまり Ｖ は最大に達しています。
　正確には、Ｅ ＝ −ｄV/ｄx で、マイナスは 高電位側から低電位側に電場が向く ことによる調整です。
　なお、ｘ₂ は、　０ ＝ ｋ・2Q/ｘ₂ ＋ ｋ・(−Q)/ (ｘ₂ − a )　より　　ｘ₂ ＝ 2ａ

　ある限られた領域内の点電荷の集合は、はるか遠く離れれば、1つの点電荷と同じこと という見方（大局的な見方）は大切です。大雑把な見方と言えば分かりやすいでしょうか。


　では、ここで問題です。　２つの点電荷 ＋２Q と −Q がある同じ状況です。

　質量 ｍ の小球 Ｐ を、ｘ軸上で点電荷から十分右に離れた位置 Ａ（ｘ≒＋∞）に置く。

　問１　Ｐ に正電荷ｑを帯びさせ、左向きの初速を与え、−Ｑ の点電荷と衝突させたい。 　　　　いくらより大きい初速を与える必要があるか。　ｋ , Ｑ, ａ, m ,ｑ を用いて表せ。

　問２　Ｐ に負電荷を帯びさせ、位置 Ａ で静かに放す。　その後の Ｐ の運動について
　　　　論述せよ。
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　解答（※�W※）は最後に







Q1.　点電荷の場合には「電位の基準を無限遠」にする必要があるという理解でいいでしょうか。


A.　公式 Ｖ＝ ｋＱ/ｒ で済ますには必要です。　でも、少し調整すれば、基準点はどこにでもできます（点電荷の位置は除いてですが）。　たとえば、上の例で ｘ＝ａ/２ を基準点にすると、無限遠の場合の電位 Ｖ から Ｖ₀ だけ差し引けばよいのです。　基準にするとはその位置での値を０にすること ですから。　もちろん、すべての点において差し引きます。　電位グラフでは Ｖ₀ だけ下へ平行移動します。

　電位の基準位置の取り方で、電位の値はコロコロ変わりますが、２点間の電位の差（電位差）は不変 に保たれます。
　電位は位置エネルギーにつながる量で、重力の位置エネルギー ｍｇｈ を思い出してもらえば、基準によって値を変えても、２点間の 位置エネルギーの差は不変 でした。


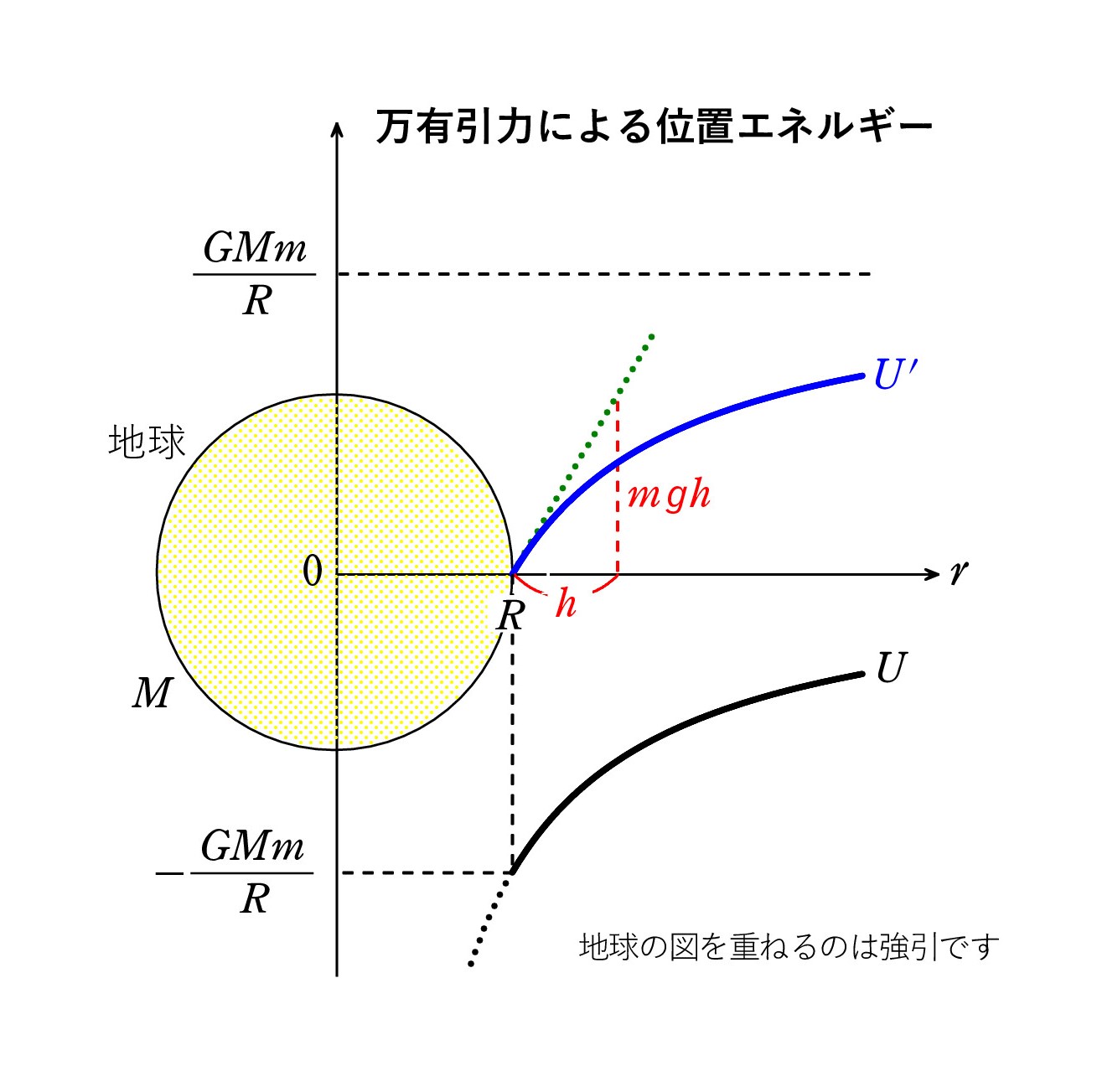　地球による万有引力の位置エネルギーは、　無限遠を基準として、 Ｕ＝−ＧＭｍ/ｒ でしたが、地球の表面を基準にすることもできます。
まず、地表での値　Ｕ₀ ＝ −ＧＭｍ/Ｒ　を確認し、
　　Ｕ‘＝ Ｕ−Ｕ₀ ＝ ＧＭｍ（１/Ｒ−１/r）
で調整終了です。
　 U のグラフを |Ｕ₀| だけ上へ上げればよいのです。

　地表からの高さを ｈ とすると、ｒ＝ R＋ｈ であり、ｈ が小さければ、Ｕ‘ ≒ ｍｇｈ となることは「エッセンス」で学びましたね（力学・問題 109 (新版は 111)）。
　　（Ｍ：地球質量　Ｒ：地球半径　ｒ：地球中心からの距離　ｒ≧R ）




Q2.　上のグラフでは、r ＝ R での接線（緑点線）が ｍｇｈ を表しているようですね。　　ｍｇｈ と万有引力の位置エネルギーの関係は頭では分かっていても、式がまるで違うし、もう一つ実感がわかなかったのですが、緑と青の関係で、見た目で分かります。　　やはり、ｍｇｈ は地表近くだけの近似ですね。　緑の直線の傾きは ｍｇ に等しいということですか。


A.　その通りです。　一般に、座標 ｘ を横軸にした位置エネルギー U グラフの接線の傾きは力 F につながります。
　正確には、　F ＝ −dU /ｄx です。　上の例は ｘ を ｒ に置き換えたケースで、
　　 F ＝ −dU /ｄr ＝ −GMｍ /ｒ² 　　まさに 万有引力です。　F ＜ ０ は引力を表し、　r ＝ R （地表）での絶対値は ｍｇ に等しいですね。

　R ≒ 6400 km もあるので、日常現象で出会う ｈ ≦ 数100 m なら、緑と青は一致していると言え、ｈ ＝ 10000 ｍ ＝ 10 km でも大差はありません。
　ついでながら、曲線の接線を考えることで、ある点の近くだけなら、複雑な関数も１次式で近似できる ということにも注意してください。

　重力の位置エネルギー ｍｇｈ は、基準点を原点とした鉛直上向きの x 軸を用いて U ＝ ｍｇｘ と表され、ばねの弾性エネルギーは、自然長位置を原点として、U ＝ k x² /２ と表されます。　いずれも ｘ で微分して、マイナスを付けてみると・・・ナルホドということになるでしょう。
　電場と電位の関係　E ＝ −dV / dx　は　F ＝ −dU /ｄx　に関連しています（ ∵　 F ＝ q E 、 U ＝ q V ）。

　話が脇道にそれ過ぎたかもしれません。脇道が大道だったものですから。
　位置エネルギー（や電位）には定数の不定性があること、定数は基準の取り方で決まること。 そして、力と位置エネルギーは不即不離 であることをつかんでくれれば十分です。
　なお、定数の不定性のお陰で、色々な位置エネルギーは足し算ですむ ことになります。 ｍｇｈ ＋ ｋｘ²/２ ＋ ｑV のように、基準点がバラバラですむ のです。






Q.　点電荷の 電場 E ＝ ｋQ/ｒ² や 電位 V ＝ ｋQ/ｒ では、ｒ ＝ ０ のとき 無限大になってしまいます。無限大の物理量はありえないように思いますが・・・


A.　ちょうど、上に万有引力の位置エネルギー U の図がありますから、まずそれを見て下さい。　U ＝ −GMｍ/ｒ ですが、この式が成り立つのは地球の表面までです。万有引力　F ＝ GMｍ/ｒ²　も同様です。
　「点電荷」は数学的な点ではなく、大きさを無視してよい帯電体ということで、
　　E ＝ ｋQ/ｒ²　や　 V ＝ ｋQ/ｒ　は帯電体の表面までの話です。

　地球に戻りますが、トンネルを掘れば、内部での F や U を調べられます。　もちろん、無限大になることはなく、　ｒ → ０ で　F → ０ になり、U → 一定 になります。
　「森」の力学の問題 43 が参考になるでしょう。

　








＃＃＃　Dialogue （対話）：　Q1 〜 Q15　＃＃＃＃＃

　　―――――　コンデンサー　・　多重極板　・　ガウスの法則　―――――



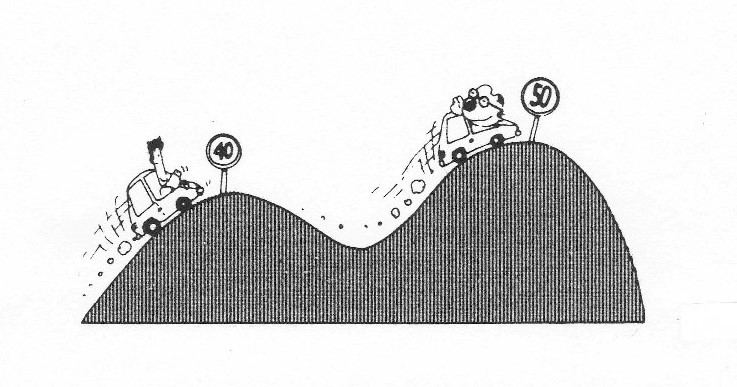
Q1.　「コンデンサーの２枚の極板上の電荷は内側の表面に存在し、一方が＋Ｑ なら、他方は −Ｑ で向かい合う」とのことです。＋と−は引き合うので、内側の表面上というのは分かります。　しかし、＋Ｑ に帯電させた極板と−2Ｑ に帯電させた極板をそれぞれ用意し、向い合わせれば、反例は簡単に作れると思いますが（図１）・・・。
　あるいは、図２のようになるのでしょうか ？　　周りからの影響はなく、極板間の電場は一様とします。

　　　　　　　

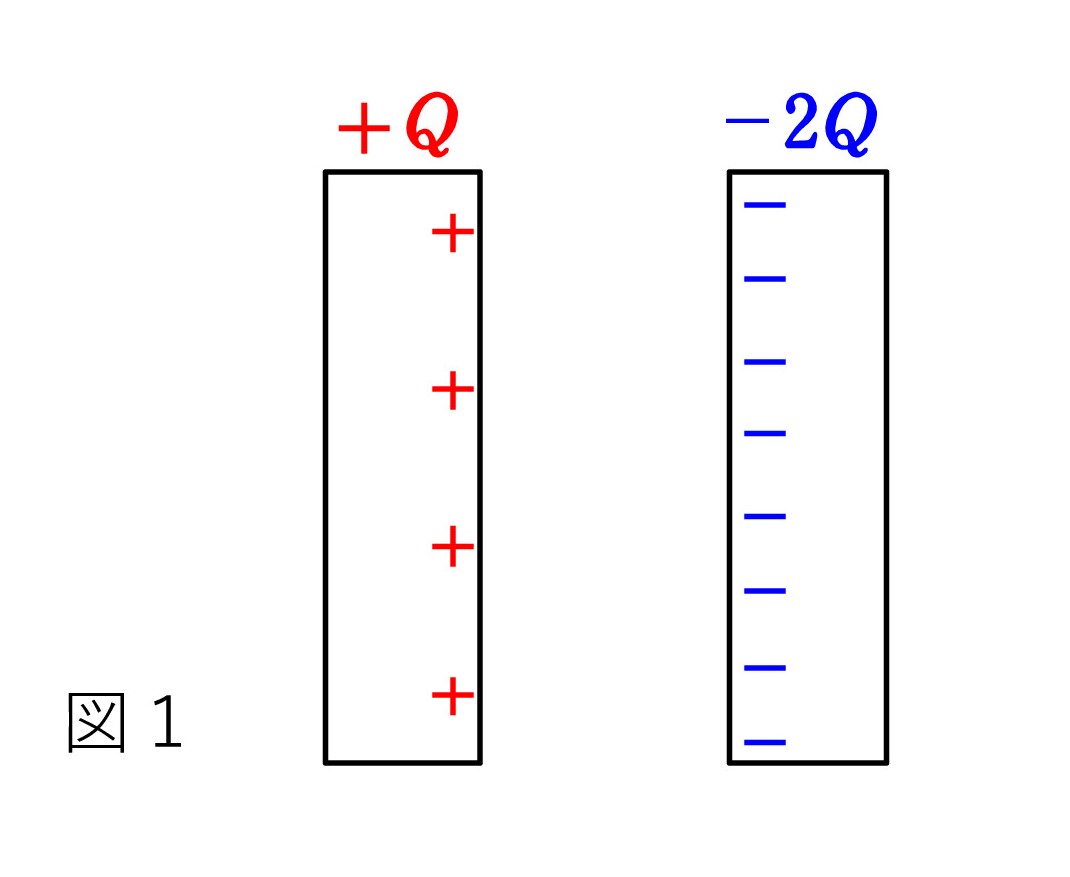
A.　いずれでもありません ！　これは金属中の自由電子のお陰で、「導体内の電場は ０」になるからです。「導体内には電気力線がない」と言い換えてもいいです。
　また、電荷は導体の内部にはなく、表面に分布 します。

　図２の場合だと、＋Ｑ と −Ｑ の間で電気力線が閉じ（ ＋ から出た力線はすべて − に入り）、周りに影響しないのですが、右端の −Ｑ が 左右から入ってくる電気力線を作り出し、左からの電気力線が極板（導体）を貫いてしまいます。
　３つの平面電荷 ＋Ｑ、−Ｑ、−Ｑ は、それぞれ左右に電気力線を発生させ、その重ね合わせが最終結果と考えてもいいです。極板を通る電気力線が残ってしまいます。

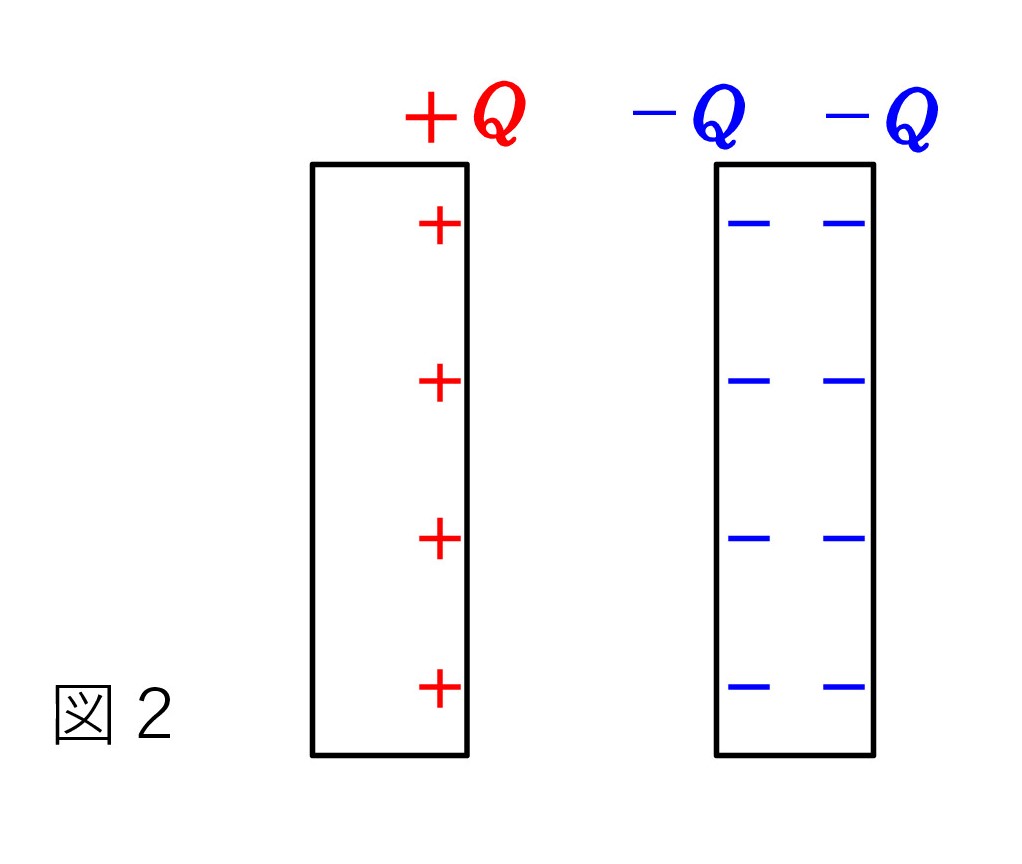
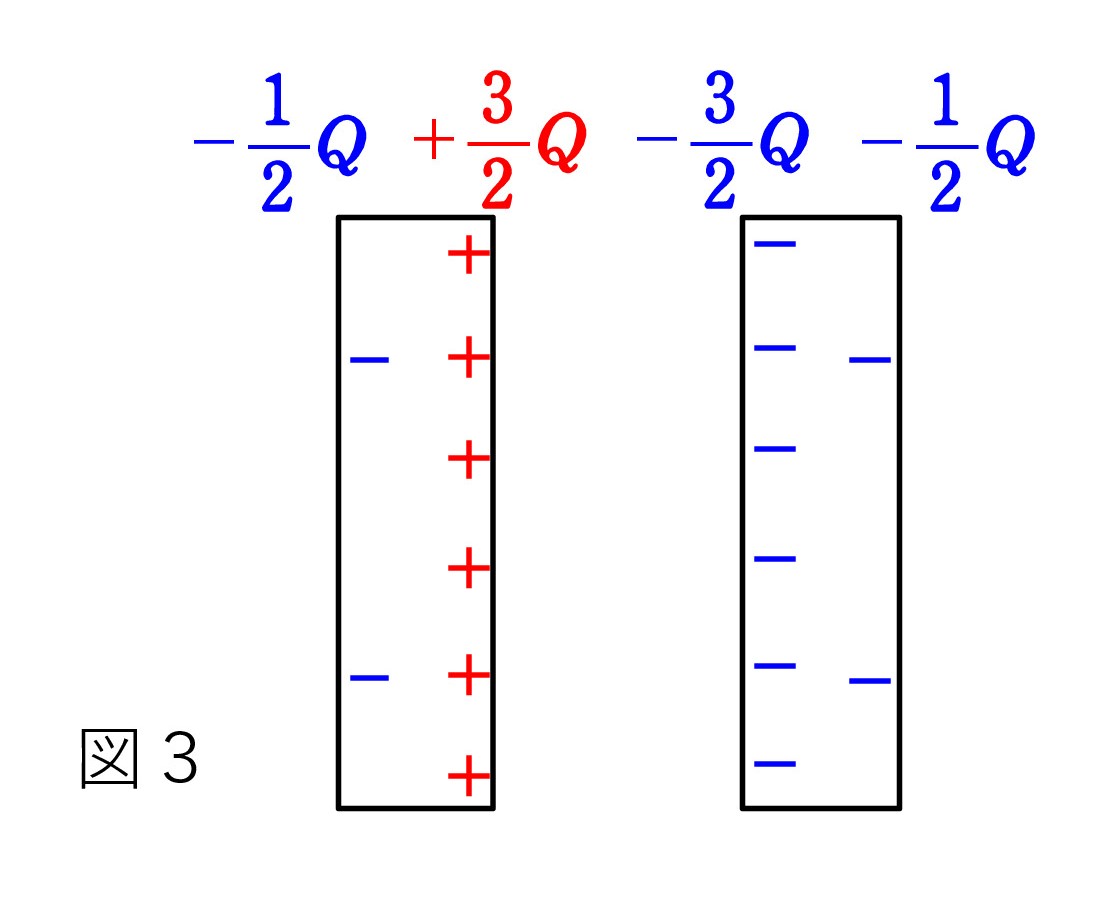　正しい配置は図３です。これなら両端の電荷 −Ｑ/２ による電気力線は、極板を含む領域では逆向きで打ち消し合うことができるのです。

　高度な話で分かりにくいかもしれません。「エッセンス」(下)ｐ67、68 (新版 p72、73) を参考に考えてみてください。
　遠くから見れば、全体は ＋Ｑ＋(−2Ｑ)＝−Ｑ に帯電し、− どうしの反発で両端に半分ずつ顔を出しているという見方もできます。

　『探究の旅に出よう』の「多重極板での電荷の配置」ではさらに一般的に扱っています。　電荷配置を簡単に決める方法にも触れています。




Q2.　「多重極板での電荷の配置」を読んでみました。　全電気量 ＋Ｑ＋(−2Ｑ)＝−Ｑ を調べて、これを２で割った −Ｑ/２ を両端にまず配置し、電荷保存を考えて、左極板の右面は ＋3/2・Ｑ 、右極板の左面は −3/2・Ｑ と決めるんですね。
　解き方は分かりましたが、やはり、最も気になることは「隣り合う極板の 向かい合った面には、＋−等量の電荷がある 」というところです。　なぜ、そう言えるのでしょうか ？
　極板が３枚以上になると、その知識がどうしても必要です。


A.　導体の性質とガウスの法則に基づいて説明できます。
　 図 a のように、２枚の極板の向かい合った面を M と N とします。　面 M に正の電荷＋が４個あるとし、１個から電気力線が１本出るとすると、４本が面 N に向かいます。 M から左へ電気力線が向かうことはありません。そこは導体で電気力線がない領域です。
　こうして４本は右の極板に入りますが、面 N 上ですべて終わらないといけません。 N より右も導体で内部に電気力線はないのです。　ここまでを示すのが 図 a です。

　　　　　

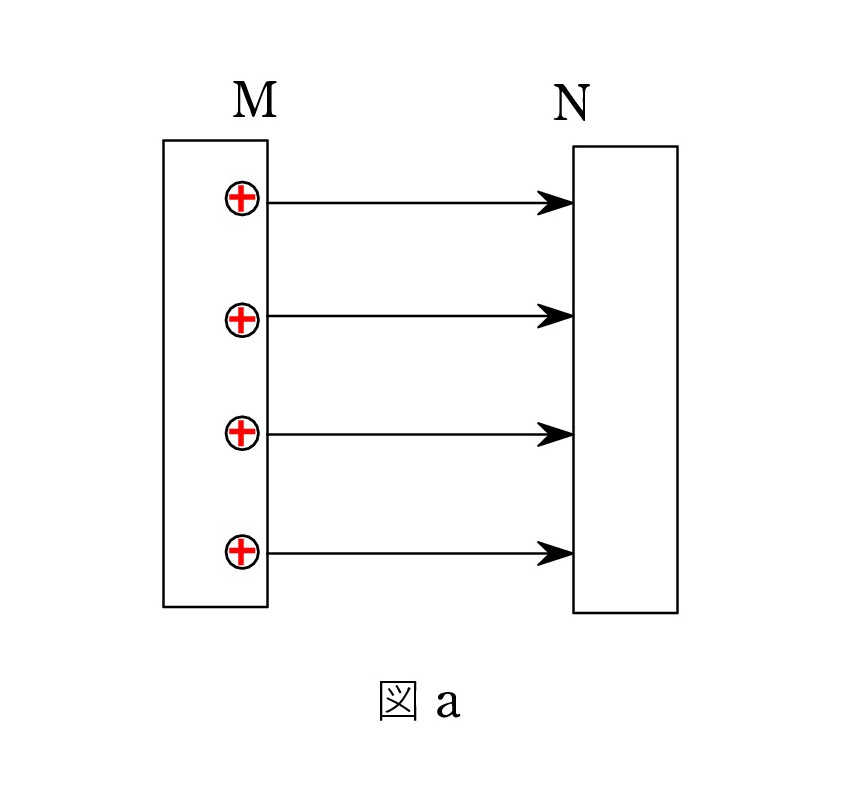
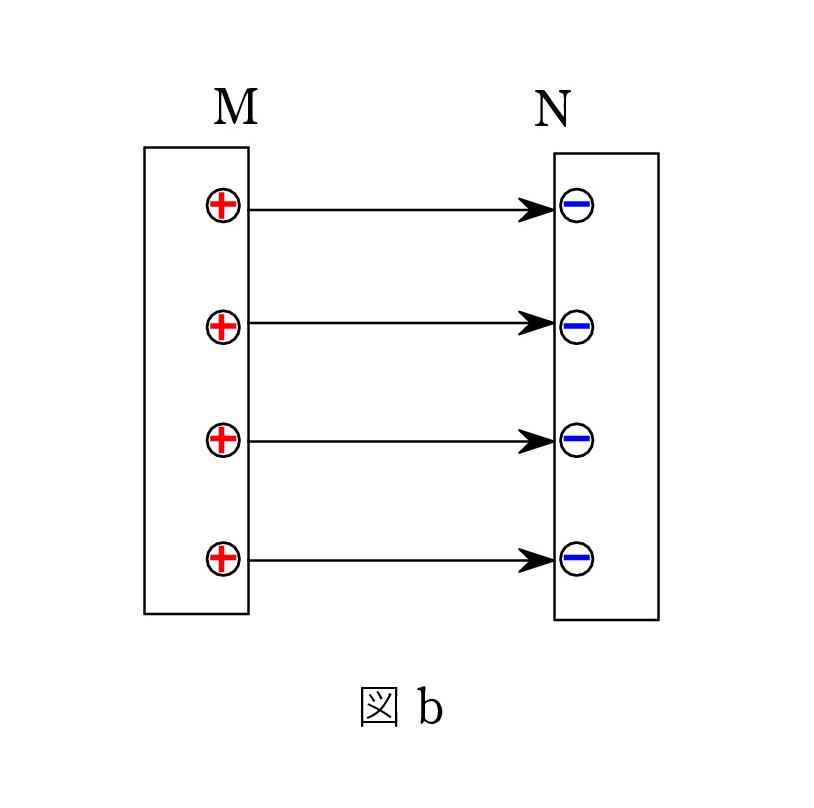
　すると、面 N には負の電荷があるはずです。　しかも４本を終わらせる（吸い取る）電荷ですから、−が４個存在することになります（図 b ）。

　以上を一般的にすれば、M が ＋Q なら、N は −Q ということになります。　電気力線の本数は Ｑ/ε 本（または 4πｋＱ 本） とすれば 正確になります（ ε：誘電率、ｋ：クーロンの法則の定数）。　　　　　（ π：パイ、円周率 ）

　極板が多数あって、それぞれが帯電していても、向かい合う極板に注目すれば、同じことです。　ただ、電荷の絶対値は 極板間でまちまちです。
　

Q3.　多重極板にとらわれて、複雑に考え過ぎていました。　今の論理からすると、任意の形状の導体が ＋Q に帯電しているとき、それを取り巻く導体があれば、その内面には −Q が生じていると言えませんか ？
　たとえて言えば、卵の「黄身」に当たる導体が ＋Q に帯電しているとき、「殻」に当たる導体の内面には −Q があるはずということです。


A.　その通りですね。　「白身」の部分に電場があります。真空ないしは誘電体に該当する部分です。

　「森」の電磁気の問題 15 では、帯電した球を取り巻く球殻のケースを取り上げています。
　そして、これも一つのコンデンサーという認識をもってください。　コンデンサーは平面極板とは限らないのです。




Q4.　 ＋Q は「黄身」の表面にあるはずですが、「白身」部分の電場は一様ではないと思えます。　電気力線は直線になるのですか ？
　また、電場の様子はどのようなものでしょうか ？　概略だけでいいので。


A.　　電気力線は曲線です。　数多くあるので、直線がないとは言えませんが。
　「黄身」の表面に垂直に出て、「殻」に垂直に入ることも意識してください。「導体は等電位であり、表面は等電位面で、電気力線と等電位面は直交する 」でした。

　「黄身」の表面積より「殻」の表面積の方が大きいので、隣り合う電気力線の間隔は広がっていきます。　「殻」に向かって電場が弱くなっていくことも分かるでしょう。「電気力線が密なところほど電場が強い 」からです。　ガウスの法則では、「（電気力線に垂直な）単位面積当たりの電気力線の本数は、電場 E に等しい」でした。




Q5.　「黄身」の導体と「殻」の導体でコンデンサーといえるのは、 ＋Q と −Q が向かい合うからですか。


A.　　「黄身」から出た電気力線がすべて「殻」に入るからです。それによって、＋Q と −Q が向かい合うことになります。

　ここからは聞き流してくれればいいですが・・・電気量 Q が２倍になると、電気力線の本数が２倍になります。　すると、電場が２倍になるので、「黄身」と「殻」の電位差 Ｖ が２倍になります。　電気量 Q と電位差 V が比例するということです。　まさにコンデンサーですね。比例定数 C が電気容量です。　 Ｑ＝ＣＶ の関係は こうしてガウスの法則から生まれています。

　各点の電場Ｅが２倍になると、電位差Ｖが２倍になる理由は 本当は少しやっかいです。　電気力線を微小区間�凾рﾉ分けると、Ｅ�凾рｪその区間での電位差です。　一本の電気力線に沿って全部集めれば、Ｖ＝ �狽d�凾рﾅす。　電場を２倍しても電気力線の形状は変わらないので、微小区間の分割に変わりはなく、区間ごとで Ｅ�凾рｪ２倍になるからです。
　頭が痛いかもしれません。　平行極板間の一様電場なら、 Ｖ ＝ Ｅｄ で アッと言う間ですが、本質は同じなので、なんとなく感触がつかめれば、それで十分です。

　先ほど電場の様子の話をしましたが、「黄身」と「殻」の間隔が狭い所の方が電場が強いのです。　電気力線が密集します。　ていねいに言えば、一つの等電位面上での比較です。「黄身」の表面とか。
　それは、一本の電気力線に沿っての式　Ｖ＝ �狽d�凾п@において、Ｖ は一定で、電気力線の長さが短ければ、 �� で寄せ集める区間の数が少ないことから想定できます。
　Ｖ が一定なのは「導体は等電位」により、「黄身」は「黄身」で、「殻」は「殻」で一定だからですし、＋ がいる「黄身」の方が高電位です。 言うまでもないことと思いますが…

　ところで、図ｂのような平行板コンデンサーの電気容量Ｃを求められますか？
　極板の面積をＳ、極板間隔をｄ、誘電率を ε とします。　もちろん 結果は公式として覚えているはずですが。

Q6.　できると思います。　えーっと・・・電気量Ｑ から電気力線が Ｎ＝Ｑ/ε 本 出て、単位面積当たりの本数が電場Ｅだから、　　Ｅ＝Ｎ/S＝Ｑ/(εＳ)
そこで Ｖ ＝ Ｅｄ を用いれば、　　Ｖ＝Ｑｄ/(εＳ)　となり、　Ｑ＝(εＳ/ｄ)Ｖ　
したがって、　Ｃ＝ εＳ/ｄ　ですね。


A.　よくできました。　試験の場合には誘導がつくはずです。　実は、今の導出で注目したいのは　Ｑ＝(εＳ/ｄ)Ｖ です。　これで Ｑ と Ｖ が比例する ことが示されているのです。　電気容量の式は、いわば、副産物 なのです。

　教科書は Ｑ＝ＣＶ を天下りに与えていますが、感心しません。　平行板コンデンサーで導けますし、先ほど話したように、ガウスの法則に基づいて一般に成り立つ関係です。




Q7.　ガウスの法則って、意外と活躍しているんですね。目立たないのは何か理由でも ？


A.　理屈っぽくなるからでしょうね。高校物理ではあえて避けている面があります。
　電気分野に入ると、学習レベルが一段とアップしている上に、ガウスの法則は抽象的・理論的に過ぎて混迷を招きます。　やはり、かなり学習が進んだ段階で学ぶべき事柄と思います。

　それと、コンデンサーといえば、平行板コンデンサーしか事実上扱うことがなく、電気容量の公式 Ｃ＝ εＳ/ｄ を用いればすんでしまうからです。 この公式のお陰で、ガウスが不要になっています。
　たとえば、「電気量Ｑの極板間の電場Ｅを求めよ」と言われればどうしていますか？
　ガウスなら、先ほどのように　Ｅ＝Ｎ/S＝Ｑ/(εＳ)　ですね。　本来の解き方です。　　でも、ふつうは　 Ｖ ＝ Ｅｄ 　と　Ｑ＝ＣＶ ＝(εＳ/ｄ)Ｖ　を組み合わせて解いています。
　コンデンサーの極板間に金属板や誘電体板を挿入したときの電気容量も、ガウスにまでは戻らず、Ｃ＝ εＳ/ｄ と 直列・並列公式で対処しています。




Q8.　大学では、ガウスの法則はクーロンの法則から導けることを学ぶそうです。　法則から導けるなら、「定理」と呼ぶべきではないでしょうか。


A.　論理的にはその通りです。　ガウスの法則の最大のメリットは、クーロンの法則が「点電荷」に対するものであるのに対し、ガウスになると、制限がなくなることです。
　本来は「定理」と呼ぶべきですが、クーロンに代わる「法則」と格上げされています。　法則の入れ替えを意図しています。　その場合、ガウスからクーロンを導くことになります（※）。
　学問の進展とともに 後から見つかったものの方がより根本的なことを表している と認識が改められることは時々あります。　でも、理論上のことですから、お話として聞き流してください。

　力学でも、運動の第２法則（運動方程式）からエネルギー保存則に達しましたが、現在では、エネルギー保存則の方がより根本的な法則とみなされています。　クーロンとガウスの関係とはちょっと違いますが。

※　点電荷 Q から Ｎ＝4πｋＱ 本 の電気力線が出て、点電荷を中心とする半径ｒの球面を貫く。
　　　球面上での電場Ｅは、　　　Ｅ＝Ｎ/Ｓ＝Ｎ/(4πｒ²)＝ｋＱ/ｒ²　
　　　その位置で点電荷ｑが受ける力Ｆは、　　　Ｆ＝ｑＥ＝ｋＱｑ/ｒ²

Q9.　クーロンの法則では２つの点電荷が直接に力を及ぼし合います。　ところが、「１つの点電荷が周りに電場をつくり、相手はその電場から力を受ける」と教科書は説明しています。　話が回りくどくなっただけで、何の役に立つのか 分かりませんでした。
　ガウスの法則では電気力線が、つまり、電場が重視されています。　法則として、クーロンが先か、ガウスが先か の議論と関係があるのでしょうか。


A.　大いにあります。　点電荷が静止しているときには 電場は回りくどいだけと言われても仕方がありません。　点電荷が動くときに違いが生じます。 クーロンの法則では「直接に」のほかに「瞬時に」力を及ぼします。　ところが、電場の変化は点電荷を中心として光の速さで伝わっていくので、遠くは元の電場のままなのです。
　いろいろな知見から電場そのものが大切だと考えられるようになりました。　そして、クーロンからガウスへと法則が移されたのです。

　今では、磁場を含めた「場」の概念が重視されています。　真空は原子や分子のない空間ですが、場は存在できるのです。　そして、ある点の場の変動は隣の点の場を変えていくというダイナミックなつながりを有しています。　電場の変動が磁場を生じ、その変動が新たな電場を生じる――という繰り返しで波として伝わっていきます。　電磁波 と呼ばれ、光の本性を表しますが、まさに場が主役です。

　ただ、光速を無限大とみなしてよい日常現象を主に扱う高校の物理では、クーロンを法則としておくのが分かりやすいでしょう。


　万有引力も「重力場」という場を介して力が伝わります。　いま、太陽が突然なくなったとします。　重力場が消え始め、光速で地球に伝わるまでに８分 20 秒かかります。その間は地球は円運動を続け、その後は力を受けない等速直線運動に入ります。円軌道の接線方向ですね。　やがて火星が、そして木星が・・・。
　もちろん、「太陽が突然なくなる」という仮定は荒唐無稽であり、「場」の説明用に過ぎません。




Q10.　導体の帯電について疑問が生じました。　卵の「殻」に当たる導体だけがあって、それが帯電しているとき、表面にあるはずの電荷は「殻」の内面と外面にどのように分布しますか ？　およそは半分ずつで、正確には表面積の比と考えていいのでしょうか。
　＋に帯電しているとして、気になるのは内面から出た電気力線です。どこへ向かうのでしょうか ？


A.　ほとんど答えの扉の前に立っている・・・というのがヒントです。　もう少し考えを進めてみて下さい。　問題にしましょう。

　 　　　　　　卵の殻状の導体が帯電しているときの電荷分布は ？

　　　　　　　　　　　　　　　　　　　　　　　　　　　　解答（※�X※）は最後に
　　　

Q11.　平行な平面からなる多重極板に戻りたいと思います。
　向かい合った面には±Ｑがいることは納得しました。　実は解法について もう一つ疑問があります。
　それは両端の電荷の決め方です。　「電荷の総和を２で割ればいい」となっています。　電荷の総合計は、向かい合った面同士では＋−消えるので、両端の２つの面の電荷の和になるはずです。　でも、両端で半分ずつになる理由は ？

　初めの回答にあった「遠くから見れば、全体は ＋Ｑ＋(−2Ｑ)＝−Ｑ に帯電し、− どうしの反発で両端に半分ずつ顔を出しているという見方もできます」というのは、確かにもっともらしい説明です。　極板が２枚ならその通りですが、枚数が多くなると、もう一つスッキリしません。　‘見方も’ とあるのは別の説明もできるということでしょうか。


A.　２つのケースを押さえてから、理由の説明に入ります。

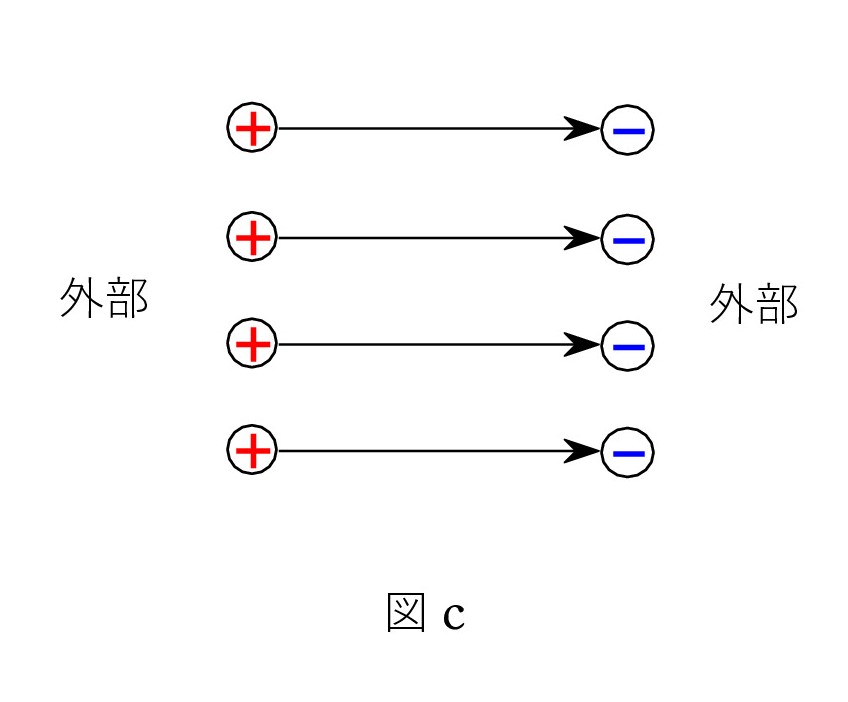
　まず、平面上の電荷 ＋Q と −Q が向かい合えば、電気力線はその間で閉じます。　つまり、電場はその間にしかなく、外部は０ということです。　仮想的な平面電荷の話であり、図ｂから極板をなくして見てほしいので、図ｃに明示します。

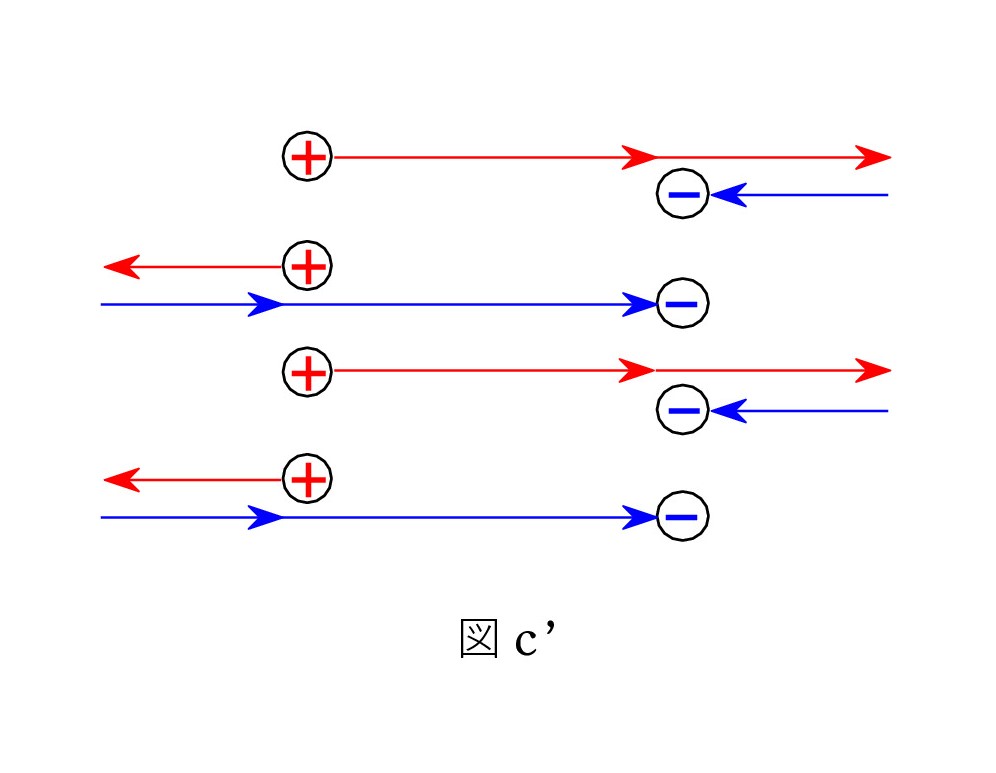
　図ｃ’ は一つの解釈です。　＋ の平面電荷は左右に半分(２本)ずつの電気力線を出し、− には左右から電気力線が入る。 それを重ね合わせたものが 図ｃになると考えることもできます。
　部分がつくる電場（電気力線）の重ね合わせが 最終電場を決める という考え方は大切です。　重ね合わせはベクトルとしてです。　一様電場に限らず成り立つ考え方です。

　　　　　

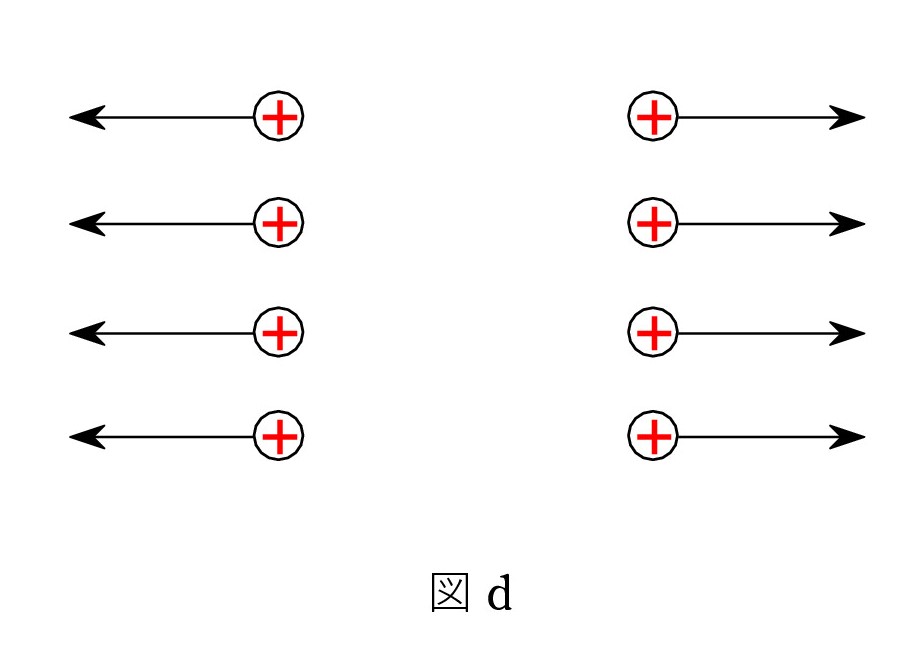
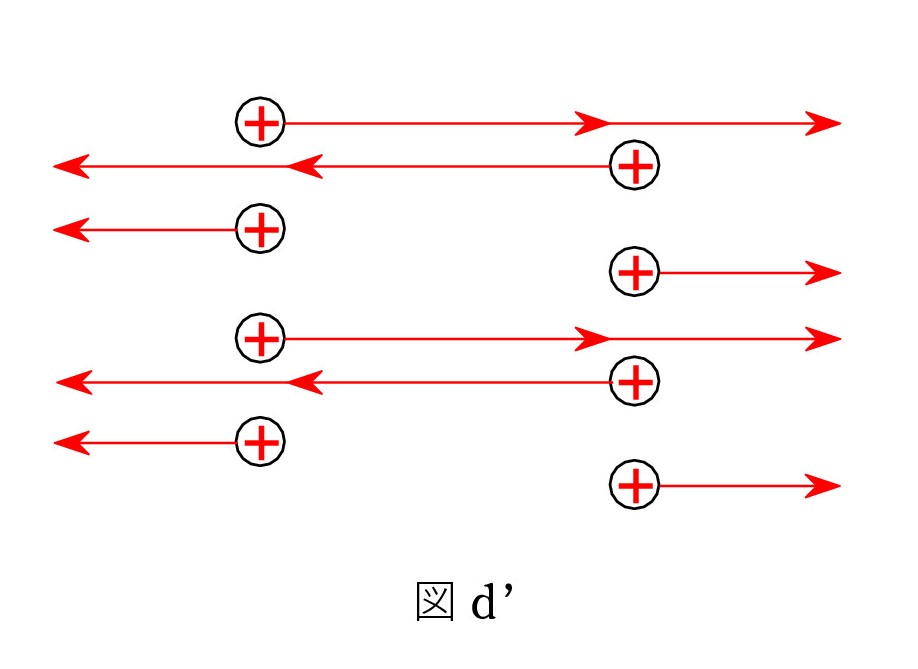
　次に、下図ｄを見て下さい。　同種の等量の平面電荷の場合には、電気力線は互いに反対側に向かって、同数だけ出現します。　これは 対称性 によります。そして、平面間の電場は０です。
　図ｄ’ のように、それぞれの平面電荷から左右に半分ずつの電気力線が出て、重ね合わせたものが 図ｄと理解してもいいでしょう。　平面間では逆向きで消えます。
　図ｄは ＋ のケースですが、− どうしでも同じことです。

　　　　　

　では、多重極板です。
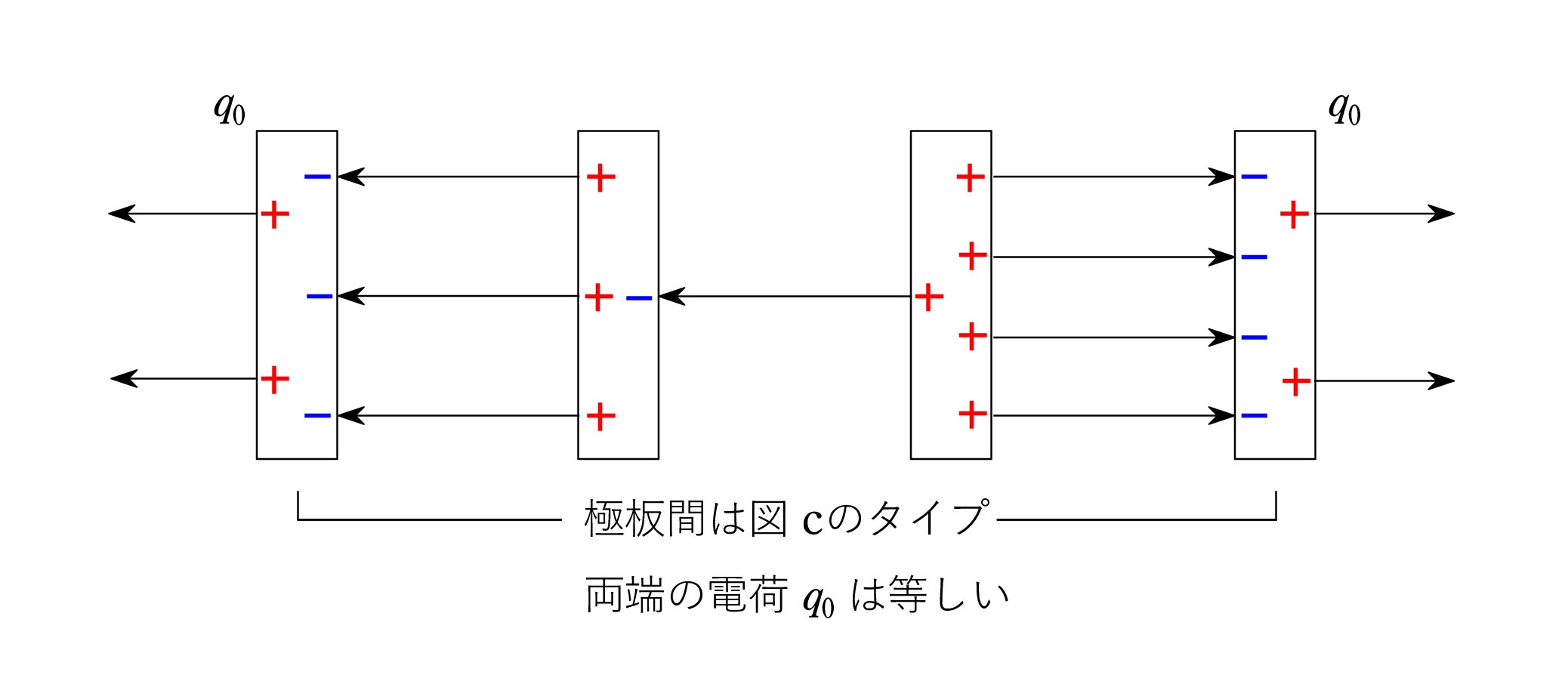
　両端の電荷さえなければ、各極板間の電場は 図ｃのように表され、全体の重ね合わせをしても、外部の位置にある導体の電場は０に保つことができます。　そこに両端の電荷ｑ₀ による電場を重ね合わせても、つまり、図ｄを重ねても、導体の電場は０のままです。
　少し手順を変えると、図ｃタイプをいくつか横に並べ、図ｄの電場のない平面間に置いてみる。　すると、多重極板と同じ状況になり、極板という導体部分の電場を０にできているのです。

　もしも、両端の電荷が等しくないと、図ｄ’ から予想できるように、両端間に電気力線が残ってしまいます。　導体内の電場を０にできないということです。

　なお、電荷配置は 極板の厚みや間隔に関係なく決まることにも注意してください。

Q12.　　図ｃのように「セット」としての特徴を生かすことが大切なんですね。
　図ｃより図ｃ' の方が精密で優れた見方だとばかり思っていました。　図ｃ' タイプの寄せ集めで考えると、多重極板全体が影響して、定性的な解読ができなくなります。　細かく分割して見るのがよいとは限らない のですね。


A.　　そういうことです。　ただ、どちらが優れているとは言えません。　両端の電荷が等しい理由は、図ｄ’ の見方で理解できました。
　図ｃ’ も 平面電荷 ±Ｑ どうしが及ぼし合う静電気力 F を考えるときには必要でした。　 図ｃでの電場をＥとすると、Ｆ＝Ｑ・Ｅ/２ です。　相手がつくった電場Ｅ/２から力を受けるからです。　コンデンサーでは極板間引力と呼ばれています。

　電気力線の作図を求められたときには、図ｃ’ や ｄ’ でなく、最終結果を表す ｃ や ｄ にしてください。　ｃ’ や ｄ’ はあくまで解釈や考察用のものです。

Q13.　だいぶ理解できてきたと思います。　そこで、問題を２つ作ってみました。

問題１：　＋Ｑ に帯電した平面極板を２枚用意し、互いに向かい合わせにする。　電荷はどのように配置するか。

問題２：　＋Ｑ に帯電した「黄身」に当たる導体の周りを、やはり ＋Ｑ に帯電した「殻」に当たる導体で取り巻く。　電荷はどのように配置するか。

　もちろん、自分なりの答えは用意していますが、確認したいので、お願いします。


A.　自分で問題を作ってみるのは、理解を深める上で大変有効な方法です。
　まず問題１は、対称性 と ＋どうしは反発し合うことからして、２枚の極板の両端（外面）にそれぞれ ＋Q が現れ、向かい合う内面の電荷は０です。　多重極板の解法に従ってもよいでしょう。　上の図では 図ｄの状況です。

　問題２では、「黄身」の表面に ＋Q があり、「殻」の内面にそれに応じて −Q が現れます。静電誘導 と見てもいいです。　電荷保存則から、「殻」の外面は ＋２Q になっています。

　問題１も２も、外部から全体を見れば、＋２Q の 一つの帯電体と見えています。　合理的ですね。


　問題２について少し立ち入った話をします。　＋Q の「黄身」の位置をずらすと、「殻」の内面の −Q の分布が変わりますが、外面の ＋２Q の分布には影響しません。
　逆に、「殻」の外部の電荷配置が変わると、「殻」の外面の電荷分布だけが変わることは 質問 Q10 で扱った問題に対しての解答でも触れました。
　内部の空間と外部の空間は 静電遮蔽 によって独立しているとも言えます。

　ただ、電荷については関係を保持していて、「黄身」の電荷は外部から見えないものの、「殻」の外面の電荷をその分増やすことで、存在を主張しています。　　符号を含めて、「黄身」の電荷を Q₁、「殻」の電荷を Q₂ とすると、「殻」の内面が −Q₁ となり、外面には Q₁＋Q₂ が現れます。　電荷保存則は基本法則 であり、電荷を遮蔽することはできません。　なお、 Q10 の場合は　Q₁ ＝０　に該当します。




Q14.　また 新しい問題を考えてみました。　多重極板の話から思いついたものです。
　卵の殻を取り巻いて殻が何重にもあるとします。　黄身とそれぞれの殻の電荷が与えられれば、配置が決められるのではないでしょうか。　各殻の内面と外面の電荷配置です。
もちろん、黄身とか殻とかは導体です。


A.　なるほど。　問題にすると、次のようになりますね。

黄身の電荷を Q₀ 、黄身を取り巻く殻 (殻１)の電荷を Q₁ 、次の殻２の電荷を Q₂ 、・・・最も外側の殻 ｎ の電荷を Q_n とする。　各殻の内面と外面の電荷配置を決めよ。

　電荷は符号を含むものとします。　具体例の方が実感がわきますが、あえて一般的にしてみました。　いかにも難しく見えます。

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　解答（※�Y※）は最後に
　　　

Q15.　電荷に符号を含めていることが大切ですね。　符号付きの式のありがたみ を改めて感じました。

　最後に、ふつうの平行板コンデンサーに戻ります。　図３のように、２枚の極板の内側では 等量の正負の電荷が向き合うことは納得しました。そこはコンデンサーになっていますが、両端は違います。
　「コンデンサー」と呼ぶときは、極板の 外側の電荷は０と思っていいのですか ？


A.　そう思って大丈夫です。　３枚以上の極板なら、両端の極板の 外側の電荷が０です。 極板 A、B、C、D なら、A と D の外側が０です。 B と C は両面に電荷があると思って対処します（極板の厚みが無視できる場合も）。
　出題者が、両端の外側が０になるようにセットします。　全極板の電気量の和が０であればよいので、回路なら、スイッチをつなぐ前は極板が帯電していなかったとか、アースするとかします。
　アース(接地）は、それにつながる極板に自由電子が過剰にあれば、電子を地面に逃がしますし、不足していれば地面から送り込みます。

　では、ここで アースに関する問題です。

　 図３（次に再掲） において、次のようにアースした場合 どうなるか、考えてください。

　　　　　（１）右側だけをアース　

　　　　　（２）左側だけをアース　

　　　　　（３）左右ともにアース

　　　　　　　　　　　　　　解答（※�Z※）は最後に
　　　






＃＃＃＃　Dialogue はここまで　＃＃＃＃

Q.　コンデンサーの極板間に金属板や誘電体板を挿入するとき、「ゆっくりと」行えば、電気の移動による電流 I は実質０であり、抵抗 R があってもジュール熱発生は無視できるとあります（森（下）ｐ70）。確かに R I² は小さくなりますが、これは１秒当たりであり、「ゆっくり」挿入すれば、時間がかかってしまうので、全体のジュール熱が無視できるかは疑問ですが・・・


A.　注意深いですね。いい質問です。こんなとき、大まかな議論が役立ちます。
　時間 T かかって挿入し、この間に電気量 Q が移動するとしましょう。　すると電流は大まかに I = Q / T です。平均的な電流とみてもいいでしょう。　そこでジュール熱は、
　 R I² × T ＝ R (Q/T)² × T ＝ R Q² / T となります。　R と Q は定数なので、この結果は、T を大きくすれば、つまり「ゆっくり」と行えば、０に近づけられるということです。
　挿入で話してきましたが、取り出しも同じことです。

　このような論法はいい加減に思えるかもしれませんが、挿入や取り出しの詳細に煩わされないので、結構有力です。極板の間隔を変える場合にも適用できますね。　この概算論法は大学ではよく用います。とくに大まかな数値を見繕いたいときに有効で、オーダー・エスティメーション (order estimation) と呼ばれています。直訳すれば「桁評価」で、細かいことは抜きにして桁が合っていればいい、有効数字1桁でいいという見方です。








Q1.　問題を解いていくと、漸化式に出会いました。　ｘ_n と ｘ_n+1 からなる式で，ｎ→∞ としたときの ｘ_∞ が問われていました。
　解けなかったので、解答を見たら、ｘ_n ＝ｘ_n＋1 ＝ ｘ_∞ として、 ｘ_∞ についての方程式に書き換えて、解かれていました。　でも、これでは不完全と思います。つまり、収束する保証が取れていません。


A.　その通りですね。必要条件だけで解いています。
　ただ、「ｘ_∞ を求めよ」という問い自体が収束を保証しているとみなせるので、
ｘ_n ＝ ｘ_n+1 ＝ ｘ_∞　として解くのは 実戦的だと思います。
　仮想実験にしろ、物理の実験がベースにある以上（現実を背景にしている以上）、収束値がないはずはないという見方もできます。

　ｘ_n 、 ｘ_n+1 、 ｘ_n+2　からなる漸化式も同様で、すべて ｘ_∞ に置き換えて、一つの方程式にします。
　もちろん、数学的にきちんと解ける場合には、減点があるかもしれませんが、わずかなものでしょう。　試験のときは、取り合えず実戦的に解き、時間が余れば厳密な解き方に挑戦するというスタイルがよさそうです。

　漸化式を扱う問題としては、コンデンサー回路の切り替えスイッチを何度も ＯＮ・ＯＦＦする問題だったり、抵抗を梯子(はしご)状に一段ずつ積み増していくときの合成抵抗の問題などがあります。

　できれば、収束が保証できる形で解きたいのですが、そうはいかないこともあります。
　その時は 迷わず利用してください。




Q2.　「森」のコンデンサーの問題 22 の解答で漸化式が登場しています。
　数学的にきちんと解く方法のほか、ｘ_n ＝ｘ_n＋1 ＝ ｘ_∞ として解く方法も紹介されています。　漸化式に頼らず、「別解」のように、定性的な考察だけで ｘ_∞ を求めてはいけないのでしょうか？


A.　問題 22 の場合、漸化式は問題文に登場していませんから、定性的判断で何の問題もありません。　むしろ、その方が物理としての価値が高いとさえ考えています。　そのあたりは、数学を重んじるか、定性的論理を重んじるか、二派に分かれそうです。

　もし、途中、漸化式で誘導されたとしても、定性的に求めるのは許されると思います。　ただ、漸化式を無視されたことに不快を感じる採点者もいないとは言えません。その場合も減点はできないでしょう。
　漸化式で誘導している場合も、解法の一つのヒントに過ぎないと思っていいケースが多い のではないでしょうか。








Q.　電磁誘導でのエネルギー保存則では「電磁力の仕事は考えなくてよい」とのことですが （『Q＆A エッセンス』）、磁場中で 導体棒が外力により 一定の速さｖで引かれているとき、力学で習った「仕事 ＝ 運動エネルギーの変化」を 導体棒に対して適用すると、電磁力の仕事なしでは 無理と思えます。　　摩擦はなく、抵抗は導体棒の分も含めてＲとします。

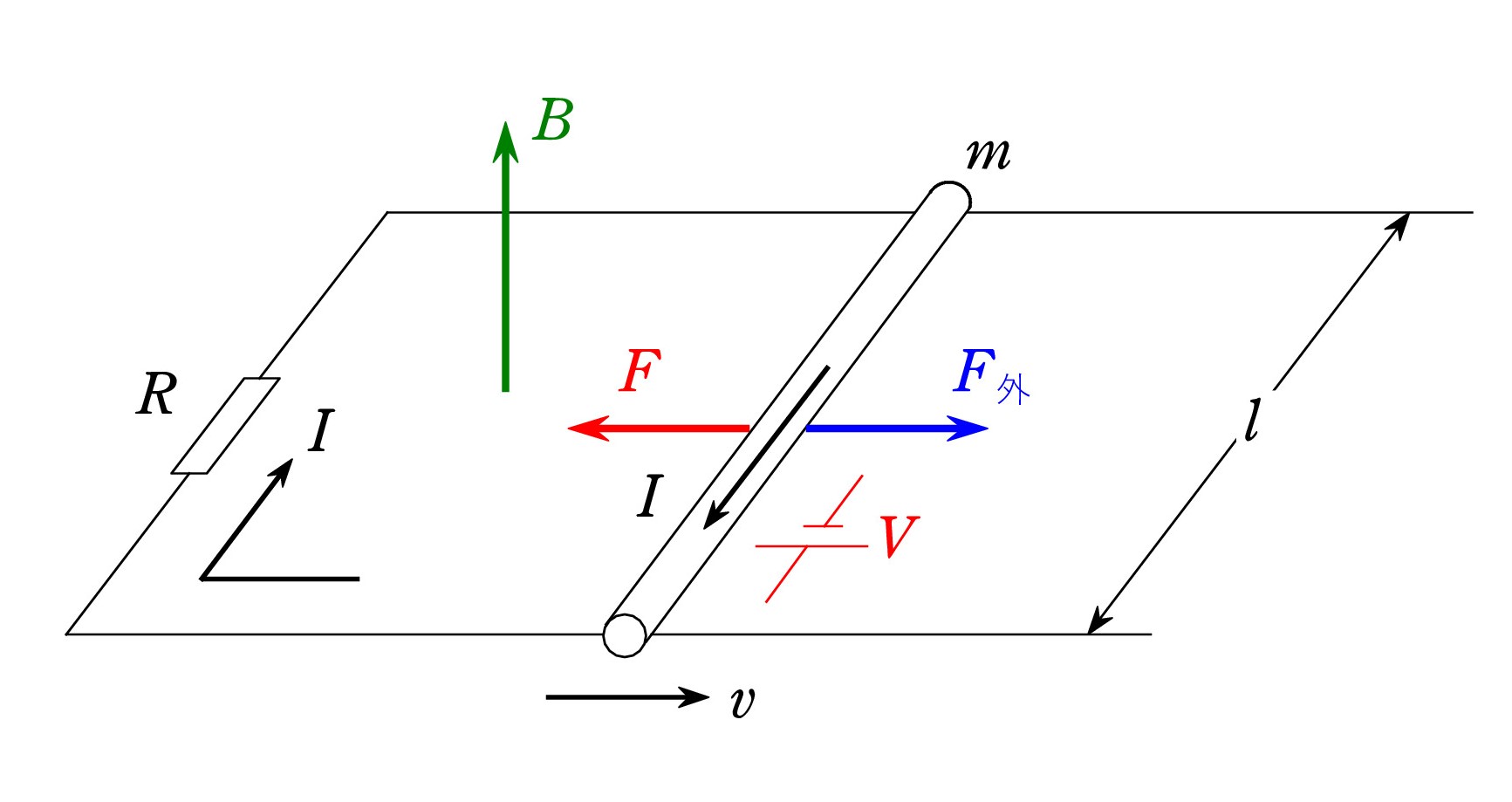
A.　その通りです。　導体棒単独では 電磁力の仕事が必要です。　速さが一定で運動エネルギーの変化がなく、
　　　　　　　（外力 Ｆ_外 の仕事）＋（電磁力 Ｆ の仕事）＝ ０
　�凾舶b間の移動距離は ｖ�凾狽ﾅあり、Ｆ ＝ＩＢｌ で 移動と逆向きなので、
　　　　　　Ｆ_外・ｖ�凾煤{（−ＩＢｌ・ｖ�凾�）＝ ０　　・・・�@　 ＜力学的側面＞

　一方、直流回路としてのエネルギー保存則は、
　　　　　　　（誘導起電力 Ｖ の仕事）＝（ジュール熱 ＲＩ²�凾煤j
　左辺は ＶＩ�凾� であり、さらに 公式 Ｖ ＝ ｖＢｌ により、上式は、
　　　　　　　　ｖＢｌ・Ｉ�凾� ＝ ＲＩ²�凾煤@　　　　　・・・�A　 ＜電気的側面＞

　�@＋�A とすると、下線部は消え、　　　Ｆ_外・ｖ�凾� ＝ ＲＩ²�凾�
　　すなわち、　　　　（外力の仕事）＝（ジュール熱）　・・・�B

　「全体に対してエネルギー保存則を立てれば、電磁力の仕事は考えなくてよい」ということです。　途中、「電磁力の仕事 と 誘導起電力の仕事 の和が ０ になる」ことも確認できました。

　ひとこと付け加えたいことがあります。　等速の場合は力がつり合い、　Ｆ_外 ＝ ＩＢｌ であり、�@ の左辺が０になって、�@ の意味が薄れています。　外力を増して加速していくような一般の状況では、�凾狽�微小とし、�@ の右辺を（運動エネルギーの変化）とすればよく、�B は、
　　　　　（外力の仕事）＝（運動エネルギーの変化）＋（ジュール熱）　・・・�B‘　
　微小時間ごとに成り立つので、長い時間でも大丈夫です。　（微小時間ごとの運動エネルギーの変化を足し合わせると、運動エネルギーの最後と最初の差になります。)

　 �B‘ も 全体を見てのエネルギー保存則として いきなり書けるようにしたいものです。　左辺が外部から与えたエネルギーで、右辺は それがどのように使われたか という観点 で書き下します。
　もし、レールに摩擦があれば、（摩擦熱) の項を右辺に加えれば 対処できます。








Q.
A.

　

※※※※※※　ヒ ン ト　※※※※※※※※※※※※※※※※※※※※※※※※※

///////////////////////////////////////////////////////////////////////////////////////////////////////

【垂直抗力の仕事の和が０になることへの ヒント 】


Ｐの変位ベクトルを２つの方向に分解する。ＰとＱはたえず接触していることに注意する。


あるいは、仕事が 力と変位の２つのベクトルの内積で表されることを利用し、ＰはＱに対して斜面方向に移動することに注意する。


元に戻る

///////////////////////////////////////////////////////////////////////////////////////////////////////

///////////////////////////////////////////////////////////////////////////////////////////////////////

【もう一つの関係式をつくるための ヒント 】


　　　ｕ，ｖ，Ｖ および θ の間の関係式をつくる。

　　　Ｐ が Ｑ に沿って運動することに目を向ける。




元に戻る

///////////////////////////////////////////////////////////////////////////////////////////////////////

///////////////////////////////////////////////////////////////////////////////////////////////////////

【 別記：　垂直抗力の仕事の和は0（内積による証明）】

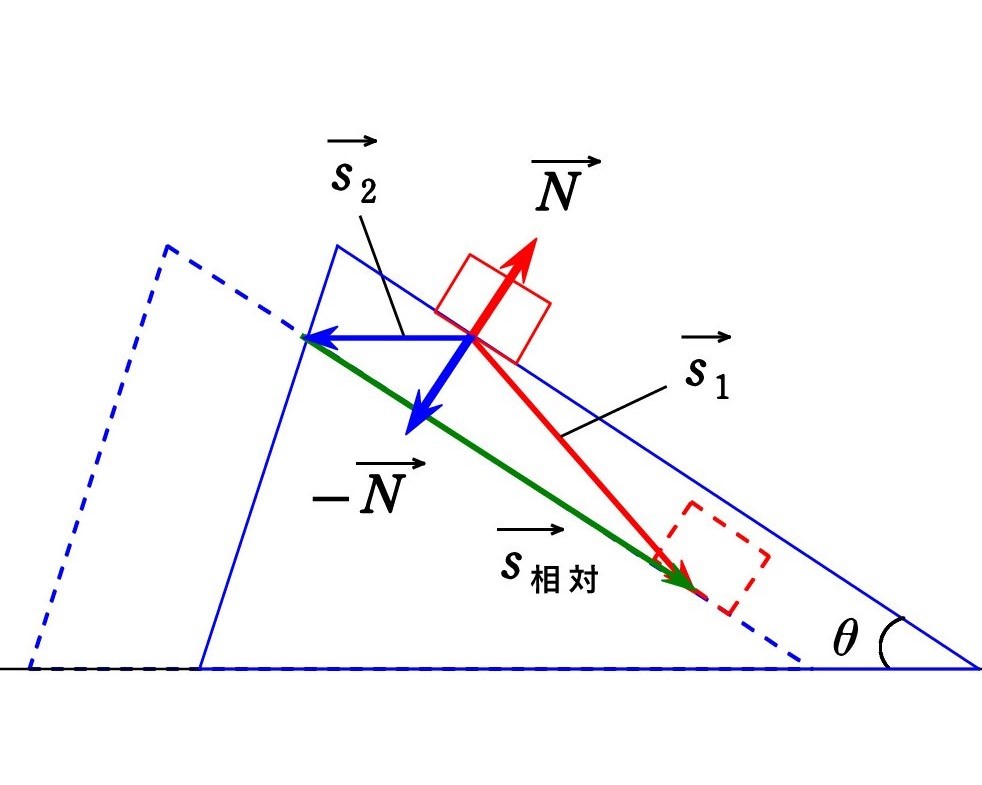　仕事の定義は　　Ｗ ＝ Ｆｓｃｏｓθ
（力の大きさＦ、移動距離ｓ、力の向きと移動の向きがなす角度 θ ）で、ベクトルの内積を用いると、
　　　　　　　Ｗ ＝ Ｆ・ｓ
と表される。(力のベクトル Ｆ、変位ベクトル ｓ)

　Ｐに働く垂直抗力を Ｎ (赤) とすると、その反作用 −Ｎ(青) がＱに働いている。
　実線から点線へと移り、Ｐ、Ｑそれぞれの変位ベクトルを ｓ₁、ｓ₂ とすると、仕事は、

　　　　　　Ｗ ＝ Ｎ・ｓ₁　　　　　　　Ｗ‘ ＝ −Ｎ・ｓ₂

　　　　∴　Ｗ＋Ｗ‘ ＝ Ｎ・ｓ₁−Ｎ・ｓ₂ ＝ Ｎ・(ｓ₁−ｓ₂）＝ Ｎ・ｓ_相対

　ここで、ｓ₁−ｓ₂ は台Ｑに対するＰの相対変位 ｓ_相対 であり、Ｑから見れば、Ｐは斜面に沿って動くので、ｓ_相対 の向きは斜面に平行になる。
　一方、Ｎ は斜面に垂直なので、Ｎ・ｓ_相対 ＝ ０　　したがって、　Ｗ＋Ｗ‘＝０


　　　　・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・

＜参考＞　ＰＱ間に摩擦がある場合の 動摩擦力の仕事

　Ｐに働く動摩擦力を ｆ （大きさｆ、斜面に沿って上向き）とし、Ｐにする仕事を Ｗ_摩擦 とする。そして、反作用 −ｆ がＱにする仕事を Ｗ’_摩擦 とすると、

　　　　　　Ｗ_摩擦 ＝ ｆ・ｓ₁　　　　　　　Ｗ'_摩擦 ＝ −ｆ・ｓ₂

　　　　∴　Ｗ_摩擦 ＋ Ｗ'_摩擦 ＝ｆ・ｓ₁−ｆ・ｓ₂ ＝ ｆ・(ｓ₁−ｓ₂）＝ ｆ・ｓ_相対

　 ｆ とｓ_相対 は逆向きで、ｓ_相対 の大きさはＬなので、　Ｗ_摩擦 ＋ Ｗ'_摩擦 ＝ −ｆＬ
　したがって、物体系から力学的エネルギーが ｆＬ だけ失われることになる。　言い換えれば、摩擦熱 ｆＬ が生じる。　摩擦熱は（動摩擦力）×（ずれた距離）とすればよいことが分かる。



元に戻る

///////////////////////////////////////////////////////////////////////////////////////////////////////

///////////////////////////////////////////////////////////////////////////////////////////////////////

【 Ｔ’ と Ｔ の比較での ヒント 】


　　　　現実の復元力は　　Ｆ‘＝ ｍｇsinθ　、　一方、単振動の場合には　Ｆ＝ ｍｇθ

　　　　　　sinθ　と　θ　の 大小関係は ？

　　　　　　そして、　周期への影響は ？

///////////////////////////////////////////////////////////////////////////////////////////////////////

///////////////////////////////////////////////////////////////////////////////////////////////////////

【 回転円板上での軌跡 】


　図１は、静止系において等速直線運動する物体が 中心Ｏから点 A に向かう様子を青で表している。　点 A に達したとき、出合う円板上の点はＡ' になる。　その途中、物体が青丸の位置に達したとき 出合う円板上の点は赤丸で示されている。
　こうして 物体が円板に描く軌跡は 赤い曲線のようになる。　円板上の観測者には 物体が赤い曲線に沿って、右にカーブして動いていくように見えるのである。

　　　　　

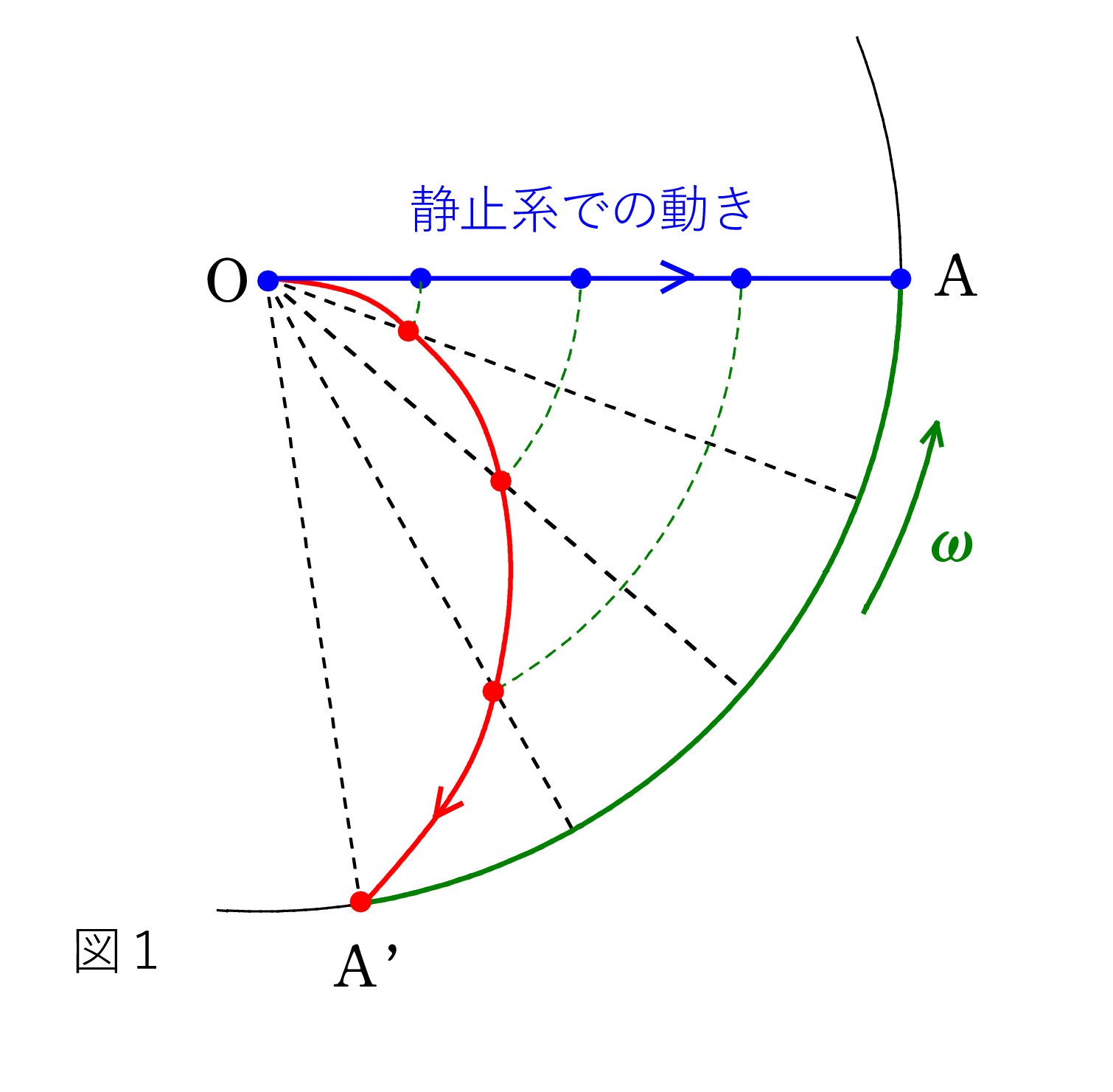
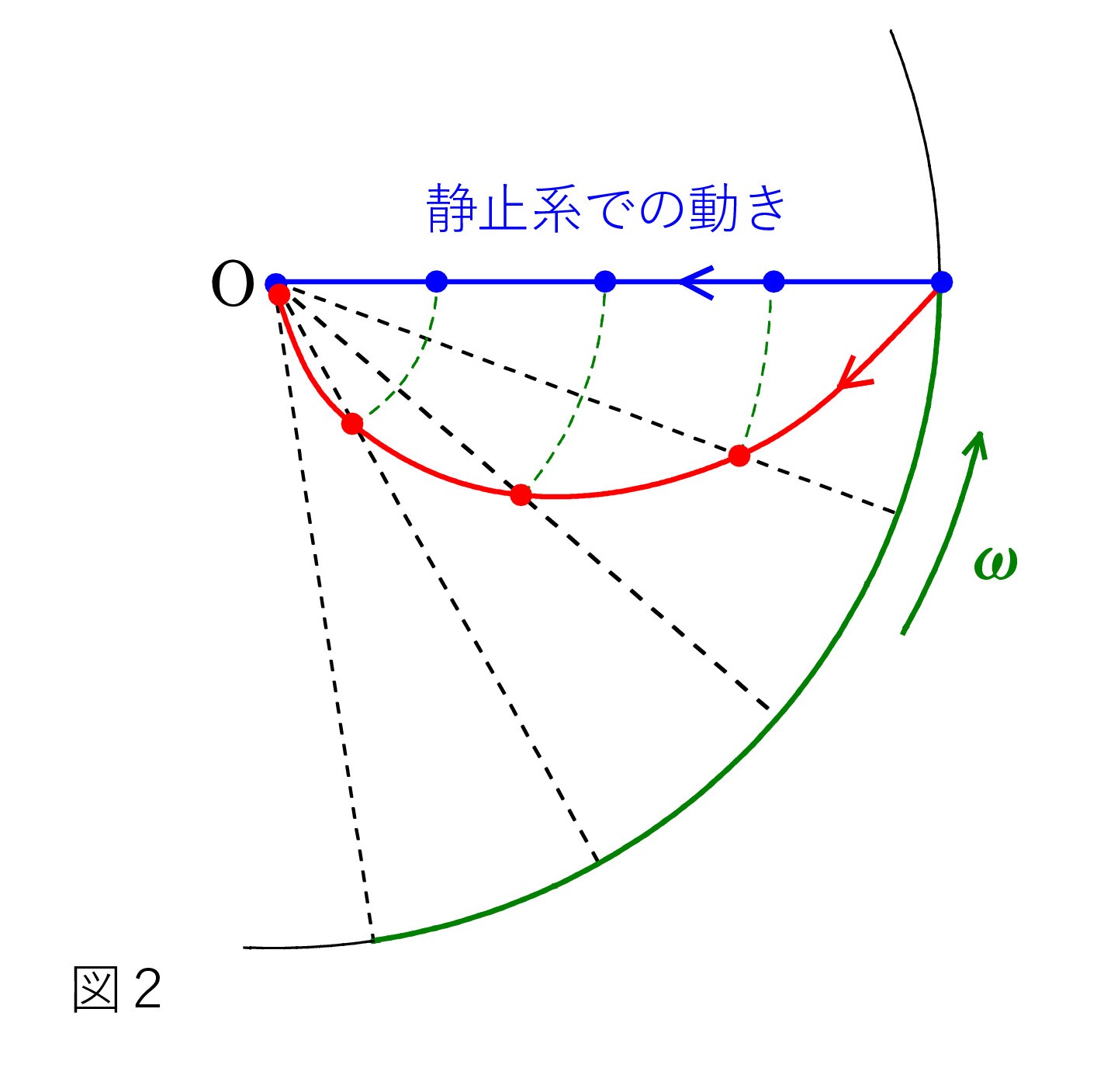
　図２は、中心へ向かう場合である。　図１と同様に 右へのカーブとなっている。
　
　等速直線運動の物体には力が働いていない。　回転円板上の観測者はカーブさせる力が働いていると認識する。　それがコリオリの力(コリオリ力)と呼ばれる慣性力である。　円板上での速度(相対速度)に比例し、速度に垂直に働くことが分かっている。
　コリオリの力は角速度 ω にも依存する。　ω が大きくなれば大きくカーブし、ω が小さくなれば直線に近づくのは、上の図からも明らかであろう。　図の扇形の角度を広げたり、狭めたりしてみれば、一目瞭然である。

　地球上で言えば、上の図は北極での状況だが、裏から見れば、南極の状況に移り変わる。　円板が透明と思えばよい。　すると、左へのカーブとなる。

///////////////////////////////////////////////////////////////////////////////////////////////////////

※※※※※※　解　 答　※※※※※※※※※※※※※※※※※※※※※※※※

※�T※【棒の重心の解答】

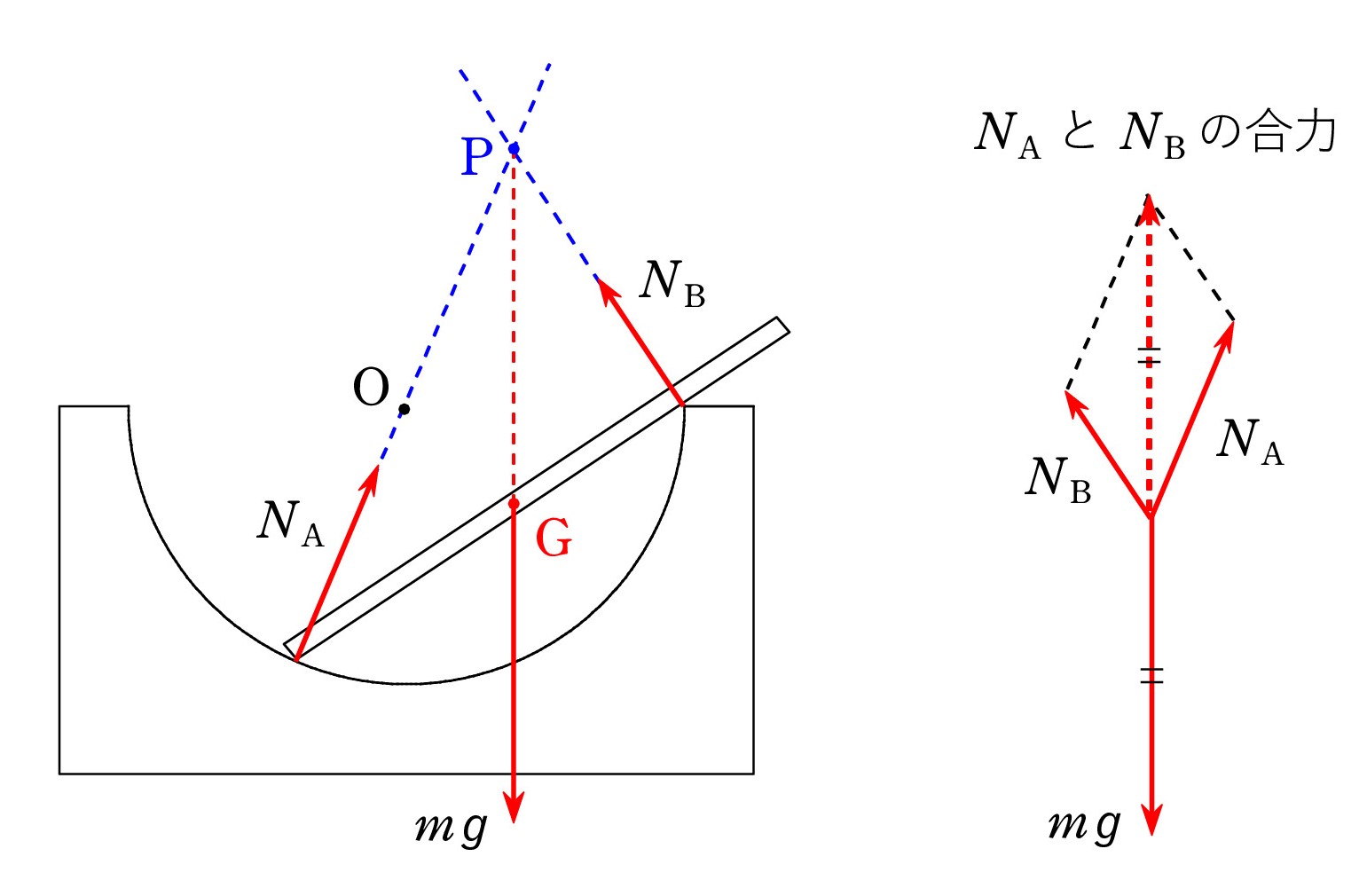　剛体が３つの力により静止している場合、力の作用線は一点で交わる という定理がある。　したがって、右図のように、２つの垂直抗力の作用線の交点 Ｐ を求め、Ｐ を通る鉛直線を考えて、重心 Ｇ が決められる。

　モーメントのつり合いでは、回転軸は剛体の外にあってもよい。
　 P を軸の位置と考えると、 Ｎ_A と Ｎ_B のモーメントは それぞれ０である（うでの長さが０だから）。　よって、モーメントのつり合いから、残りの 重力のモーメントも０でなければならない。　それは、重力の作用線が P を通ることを意味する。
　この定理が成り立つためには、３つの力が平行でないことが必要である。

　一様な棒の場合には、G は棒の中点と一致することになる。
　力のつり合いから、３つの力のベクトル和は０になる ことも意識してほしい。















※�U※【慣性力の図解】

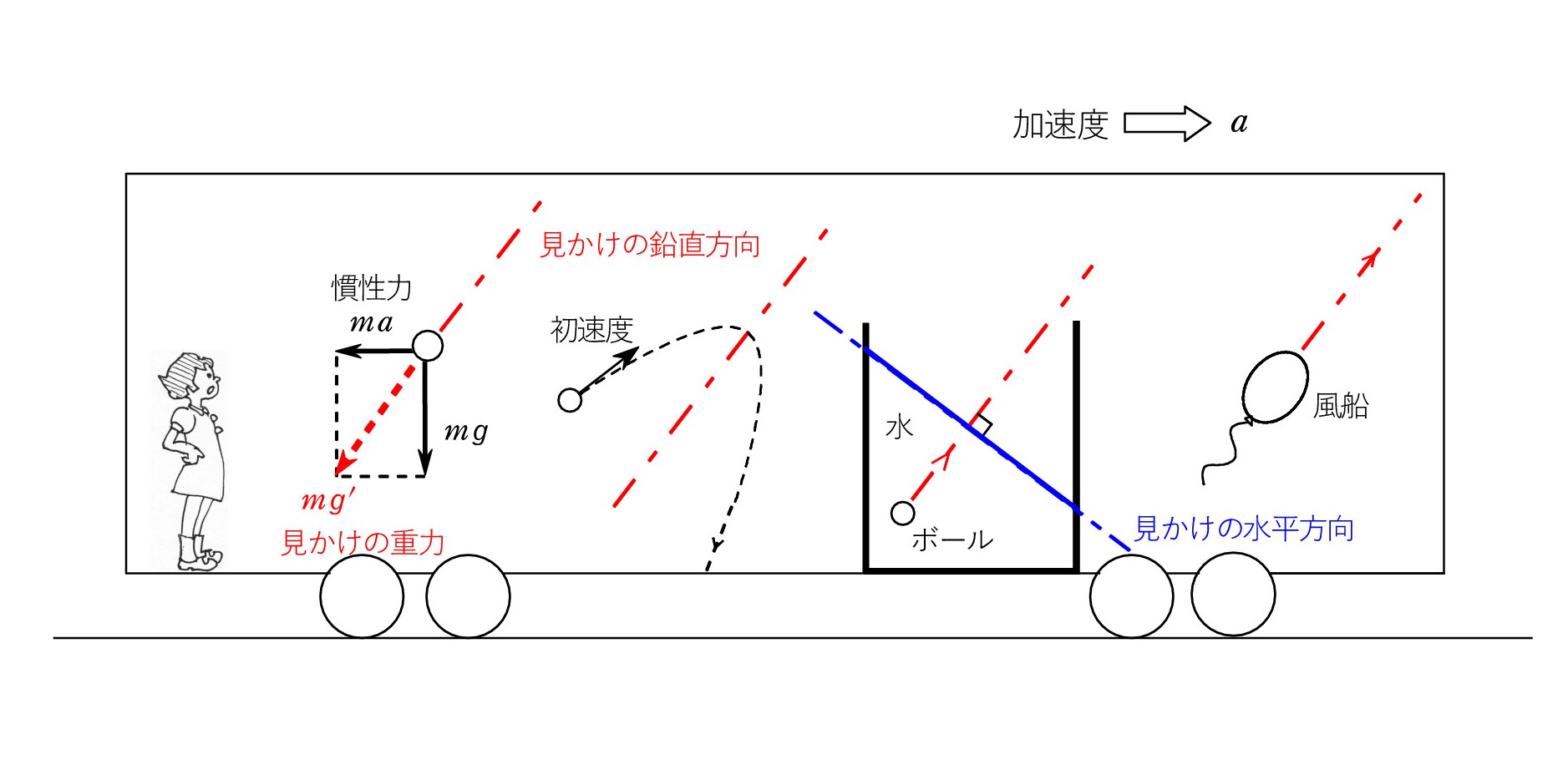
　　　　　慣性力は左向きなので、ボールや風船は左上に動くという誤解が多い。
　　　　　水や空気にも慣性力が働いていることを見落としている。
　　　　　 浮力を生み出しているのは水や空気である。














※�V※【摩擦がある場合の 式の成立・不成立 の解答】

　　(a) 　�@　〇　　�A　×　　�B　〇
　　(b) 　�@　×　　�A　×　　�B　〇
　　(c) 　�@　×　　�A　×　　�B　〇

�@：　運動量保存則は、水平方向で外力がないこと、つまり、床からの摩擦がないことが条件。　PQ 間の摩擦は内力であり、構わないので、(a)だけが OK 。この判断はぜひできるように。

�A：　摩擦があれば、力学的エネルギー保存則は壊れるので、すべてダメ。
　(a)の場合、摩擦熱 μＮ・Ｌ を右辺に加えれば、エネルギー保存則として成立するようになる（μ：ＰＱ間の動摩擦係数)。　摩擦熱は ずれた(擦れ合った)距離を用いる。
　ただ、垂直抗力Ｎが分かっていないので、すぐに役立つわけではないが、摩擦熱の取り入れ方は身につけておきたい。　（別記 の＜参考＞を参照）

�B：　摩擦に関係なく、Q から見れば、P は斜面方向（ θ 方向）にしか動かないので、すべて OK 。
　(c) で �B を × にした人が多いのではなかろうか。 (a)・(b)からの流れで、条件が悪くなれば × が増えるはずと、× にしてしまう。　いわゆる「ひっかけ」であるが、本当に（確信をもって）分かっているかどうかが試されている。
















※+※【 θ₁ ＋ θ₂ ＝ 90° の 作図での証明 】

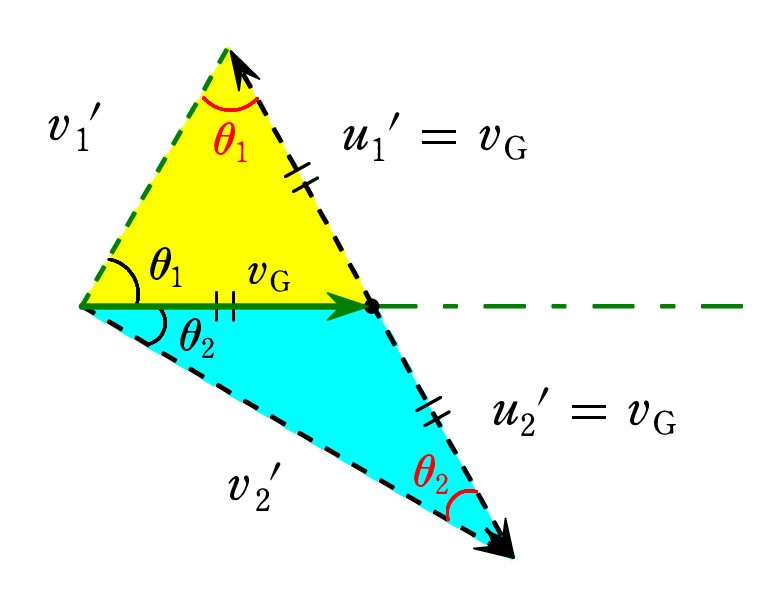　図４と同様、空色の三角形は二等辺三角形。
　ボールの質量を m とすると
　　 v_G ＝ (ｍv₁ ＋０)/(ｍ ＋ ｍ) ＝ v₁/2　
　そこで、球１について、　u₁ ＝ v₁ − v_G ＝ v₁/2　
　また、衝突後について、　　 u₁’＝ u₁ 　
　よって、 u₁’＝ v_G 　　これに注意して図４を描き直すと、右のようになる。
　「質量の逆比」から　u₁’＝ u₂’（＝ v_G）としてもよい。

　黄色の三角形も二等辺三角形であり、赤字で示した θ₁ と θ₂ が現れている。
　全体の三角形に対して、　 θ₁ ＋( θ₁ ＋ θ₂ )＋ θ₂ ＝180°　　∴　 θ₁ ＋ θ₂ ＝ 90°














※X1※【 Ｔ ’と Ｔ の大小の解答 】

　　　　　　

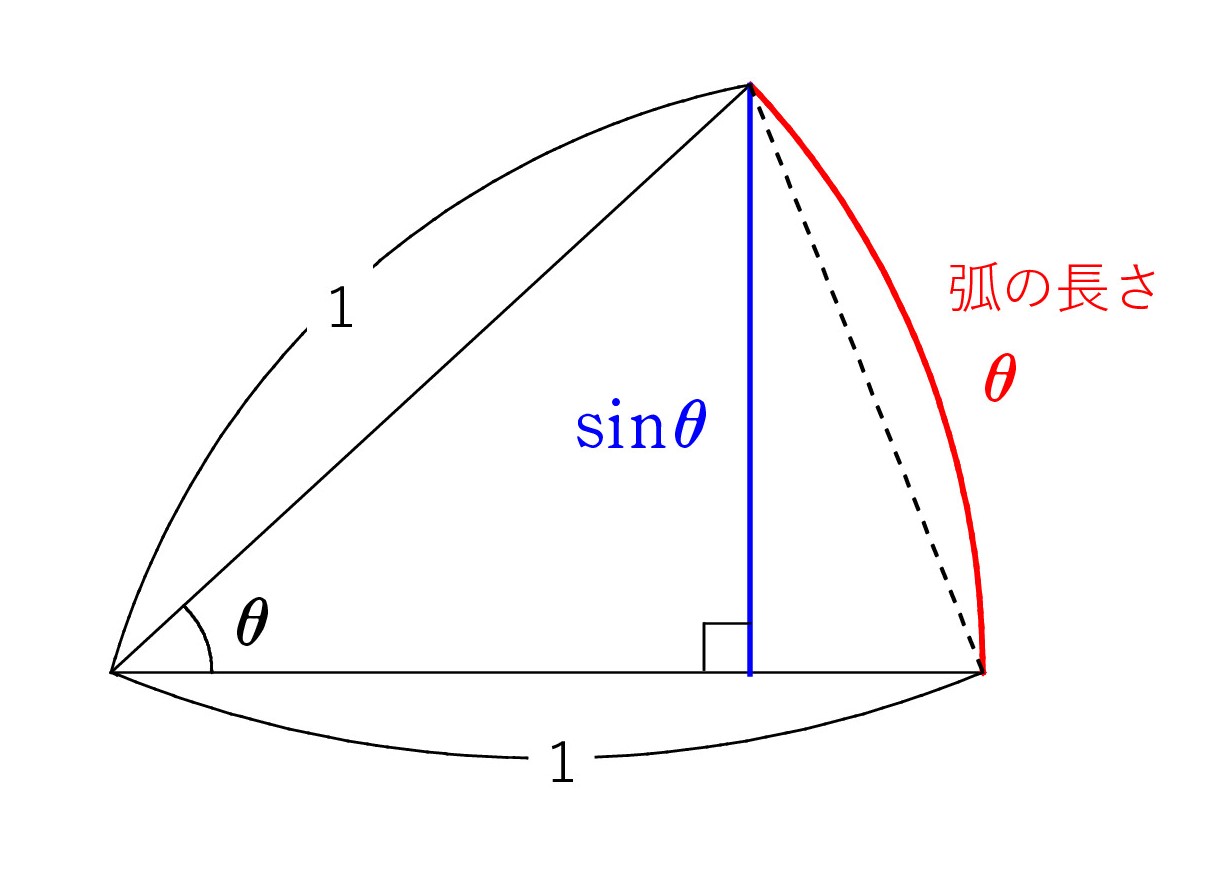
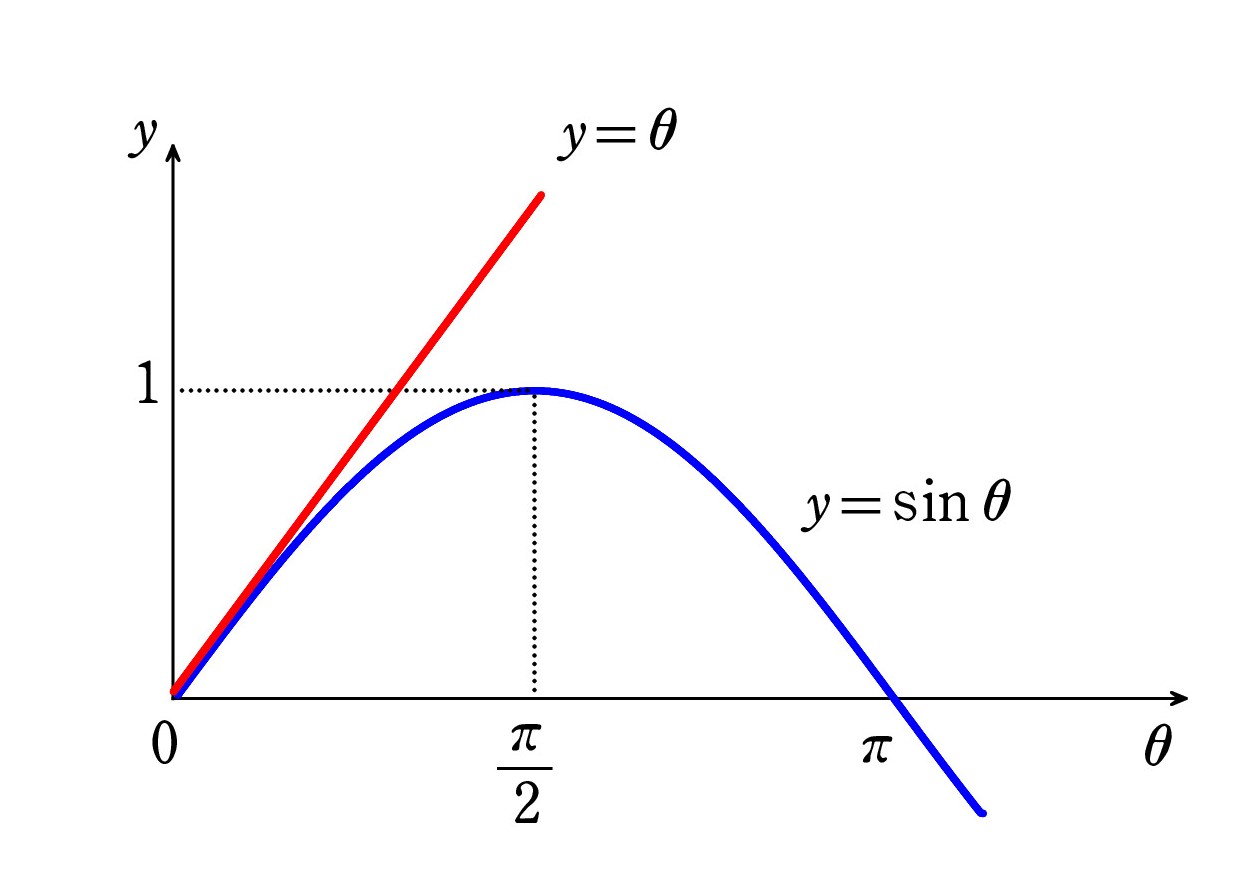
　左の図のように　sinθ ＜ θ　（ sinθ ＜ 点線の弦の長さ ＜ θ ）
　右のグラフをイメージしてもよい。　　θ が微小のときは、sinθ ≒ θ であること、θが大きくなると、sinθ ＜ θ　だけでなく、２つの差が広がっていくことが分かる。

　したがって、　　Ｆ‘ ＜ Ｆ

　現実の復元力 Ｆ‘＝ ｍｇsinθ は、単振動に必要な復元力 Ｆ＝ ｍｇθ より弱いので、時間がかかる。
　たとえば、振動の端から中心に戻るまでの時間（周期の１/４）が長くなる。

　Ｔ‘ はＴより長くなる。


「振幅が大きいと、長い距離を動くので、時間Ｔ' は長くなる」という解答は 認められない。　単振動のとき周期Ｔが一定になっているのは、振幅が大きいと、速さ(同じ位置での速さ)が大きくなっていることによる。　距離と速さという２つの要素が絡むのに、距離しか考慮していないからである。

　ここでは、現実の振り子と単振動できる仮想的な振り子を、振幅を等しくして比較したい。　前者は　Ｆ‘＝ ｍｇsinθ　によって振動し、後者は　Ｆ＝ ｍｇθ によって振動する。　振動の端から同時に放したとすれば、力の大きなＦの方が、加速がよく、速さも大きくなって、振動中心に早く達する。














※X2※【 グラフの描き方の解答 】

　２つの量の関係は直線グラフになるかどうかが分かりやすい。
　そこで、Ｔ＝ ＝ 2π √(ｌ/ｇ) の両辺を２乗して、　　　Ｔ²＝４π²ｌ/ｇ
　よって、　横軸をｌ、縦軸をＴ² とすればよい。　縦横は逆でもよいが、変数ｘを横軸にし、ｘの関数ｙを縦軸にするのがふつう。

　ケプラーの第３法則は　Ｔ²/a³ ＝ 一定　と表される（Ｔ：惑星の公転周期、　a：半長軸）。　この場合は、横軸に a³ を、縦軸に Ｔ² をとって、いろいろな惑星のデータをプロットすれば、直線に乗るはずである。


　２つの量 ｘ と ｙ の関係が　ｙ＝ｋｘⁿ　のように表されることは多い（ｋは定数)。
単振り子の周期Ｔなら　ｎ＝１/２　であり、ケプラーの法則の公転周期Ｔなら　ｎ＝３/２　となっている。　いま、ｘ と ｙ の実験データがいくつもあり、　ｙ＝ｋｘⁿ　の関係にあるかどうかが不明とする。　このとき、

　横軸、縦軸 共に 対数目盛りのグラフ にプロットしてみる。
　各点が直線に乗れば、ｙ＝ｋｘⁿ の関係にあると言え、さらには ｎ の値が決められる。
　その根拠は ？


　　　　　・・・・・・・・？・・・？・・・？・・・？・・・？・・・・・・・・


　ｙ＝ｋｘⁿ　の両辺の対数をとると、　logｙ＝ logｋ＋ｎlogｘ
　つまり、横軸を Ｘ ＝ logｘ とし、縦軸を Ｙ ＝ logｙ としたグラフ上では、
　Ｙ ＝ ｎＸ ＋ 定数　であり、直線グラフになる。　その傾きから ｎ が読み取れる。

　大変便利なグラフであり、縦横に(常用)対数目盛りを書き入れた両対数方眼紙が市販されている。　本来の用途は、何桁にもわたって幅広く分布する数値をプロットするためのものであり、縦軸だけが対数目盛りのものもある（片対数方眼紙）。














※X3※【 振り子の長さ調整の解答 】

　１日（24×60分＝1440分）に１分進むということから、周期Ｔを １/1440 だけ 調整してやればよい。　周期の増加を�凾sとすると、�凾s/Ｔ＝１/1440

　振り子の長さを�凾撃ｾけ長くしたとき、

　　　Ｔ＋�凾s＝ 2π √((ｌ＋�凾�)/ｇ)＝ 2π √(ｌ/ｇ)・√(１＋�凾�/ｌ)
　　　　　　　＝ Ｔ(１＋�凾�/ｌ)^1/2 ≒ Ｔ(１＋ 1/2 × �凾�/ｌ)

　　　∴　�凾s≒Ｔ�凾�/2l　　∴　�凾�/ｌ≒２�凾s/Ｔ＝２×1/1440＝１/720

　分数として異なっていても、小数に直したとき、0.0014 ぐらいになっていればよい。

　近似するときの方針は、「１＋微小量」の形を目指すこと。
　その際、元の形（この場合は Ｔ＝ 2π √(ｌ/ｇ)）を先頭に取り出してみる（強引にセットする)とよい。

　変化後の式　Ｔ＋�凾s＝ 2π √((ｌ＋�凾�)/ｇ)　を 元の式　Ｔ＝ 2π √(ｌ/ｇ)　で 辺々で割る手もある。
　この場合は、　１＋�凾s/Ｔ ＝ √(１＋�凾�/ｌ)　となり、
右辺を近似して　１＋ 1/2 × �凾�/ｌ　であり、　�凾s/Ｔ＝�凾�/2l　が得られる。


　実際には、長さを調節するねじを、長くする方向に適当に回して、様子を見ることになる。　「いい加減では？」という非難に対しては、「 徐々に正しい長さに近づけていく」と答えることに。　途中、行き過ぎ(修正し過ぎ)が起こるのがふつうであるが、気にしない。　工学では 最重要と言ってよい 実用的な手法 である。














※X4※【 地点Ａの解答 】


　地点Ａは北回帰線上にある。

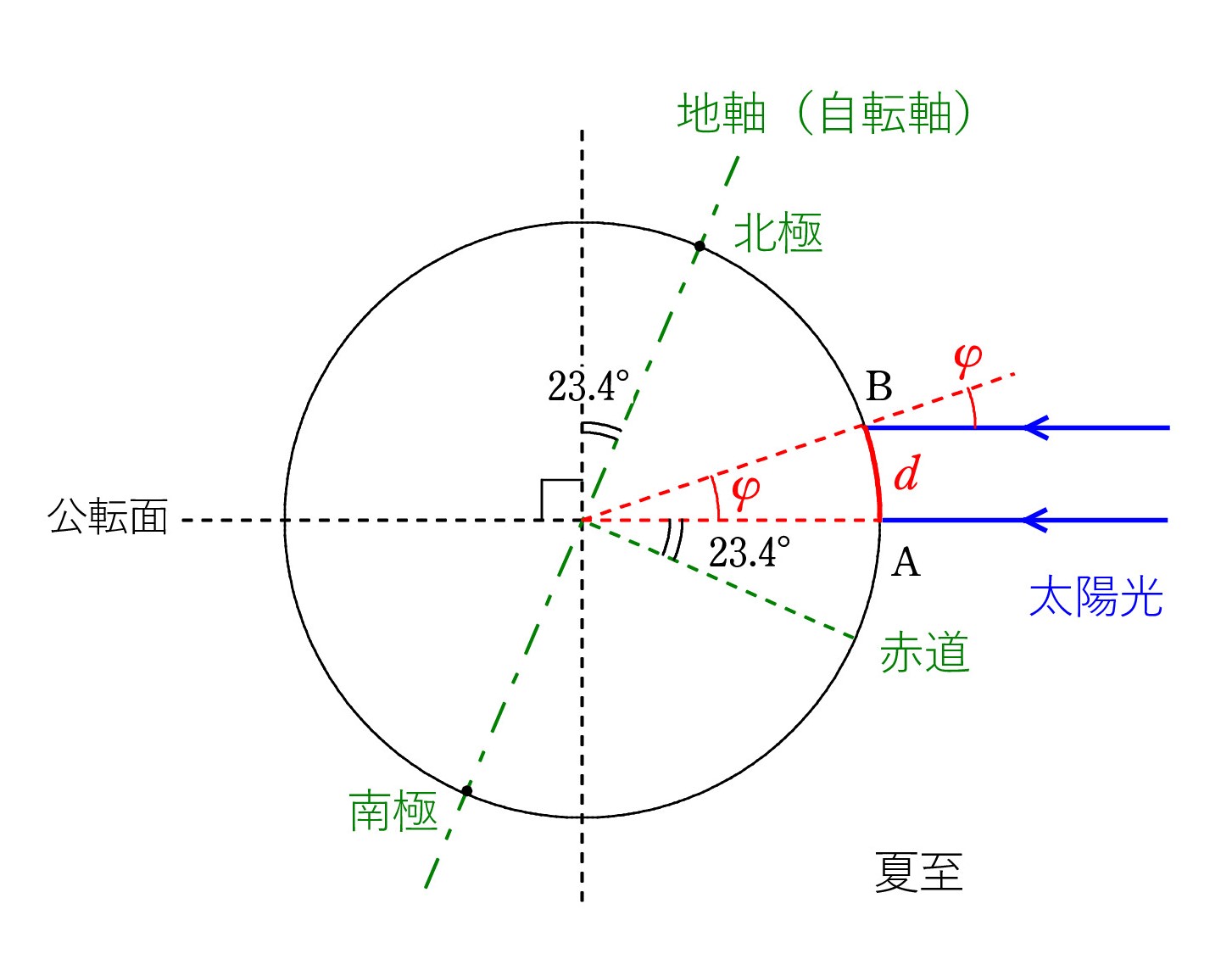　夏至に太陽が真上に来るのは、北緯23.4°の土地である。23.4°は地球の自転軸の傾きに当たる。　赤道をはさんで、南北23.4°の範囲では、太陽が真上に来ることがある。 赤道上なら、春分と秋分に真上に来る。　もちろん、南中時、昼の12時に。　立っている物の影がなくなるので、印象的である。

　アレキサンドリアにいたエラトステネスは、800km ほど南にあるシエネの町では夏至の日に太陽が真上から照らすことを聞き知って、考えついた。　アレキサンドリアにいたまま夏至の南中時に棒を立て、φ が測れることを。

　ちなみに、地中海に面するアレキサンドリアでは太陽が真上に来ることはないので、シエネの話が興味深かったのであろう。それも、夏至という特別な日の出来事なのだから。そのお陰で「同時に」測ることができた。　紀元前３世紀のこと。

• 太陽が真上に見える場所と時期
　　（入試には無関係です）

※X5※【 連星の質量の解答 】


　万有引力Ｆは、恒星間の距離 ｒ₁＋ｒ₂ で決まることに注意する。
　　　Ｆ ＝ ＧＭ₁Ｍ₂ / (r₁＋r₂)²　　　作用・反作用により、両星共にＦの力を受ける。
　周期Ｔが等しいことも大きなポイントになる。

　　　　　　

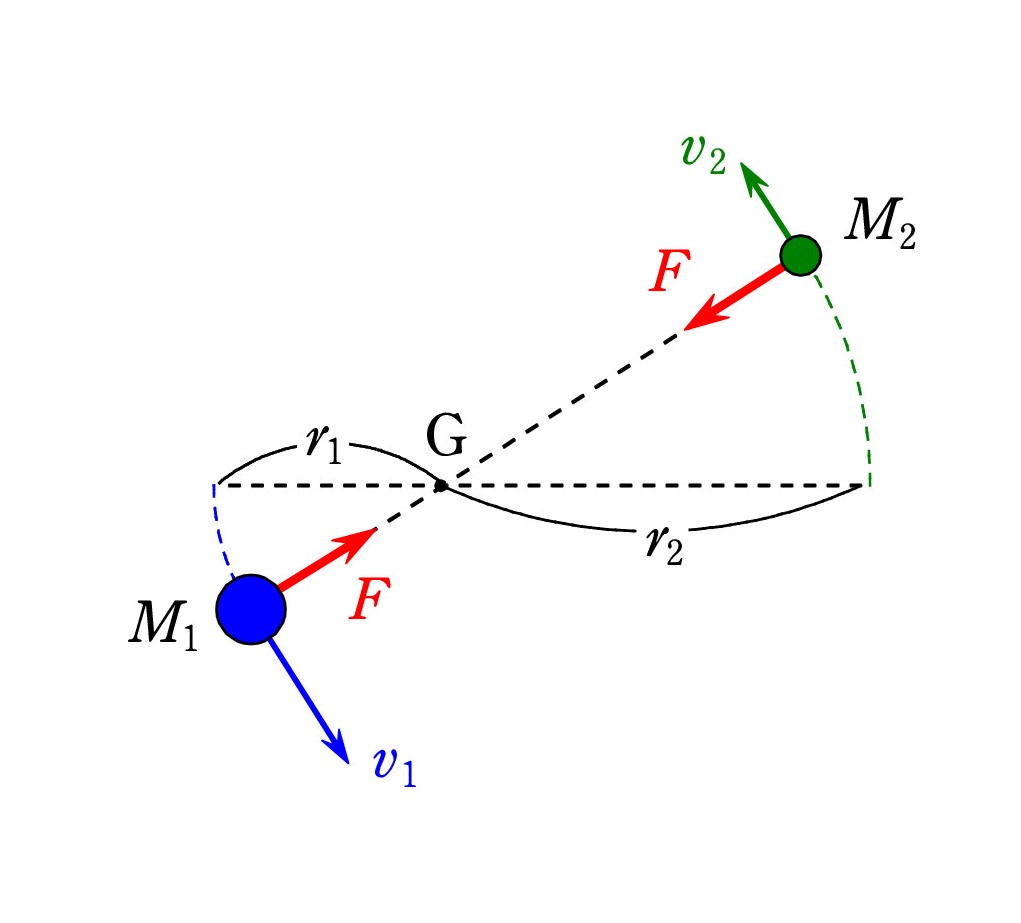
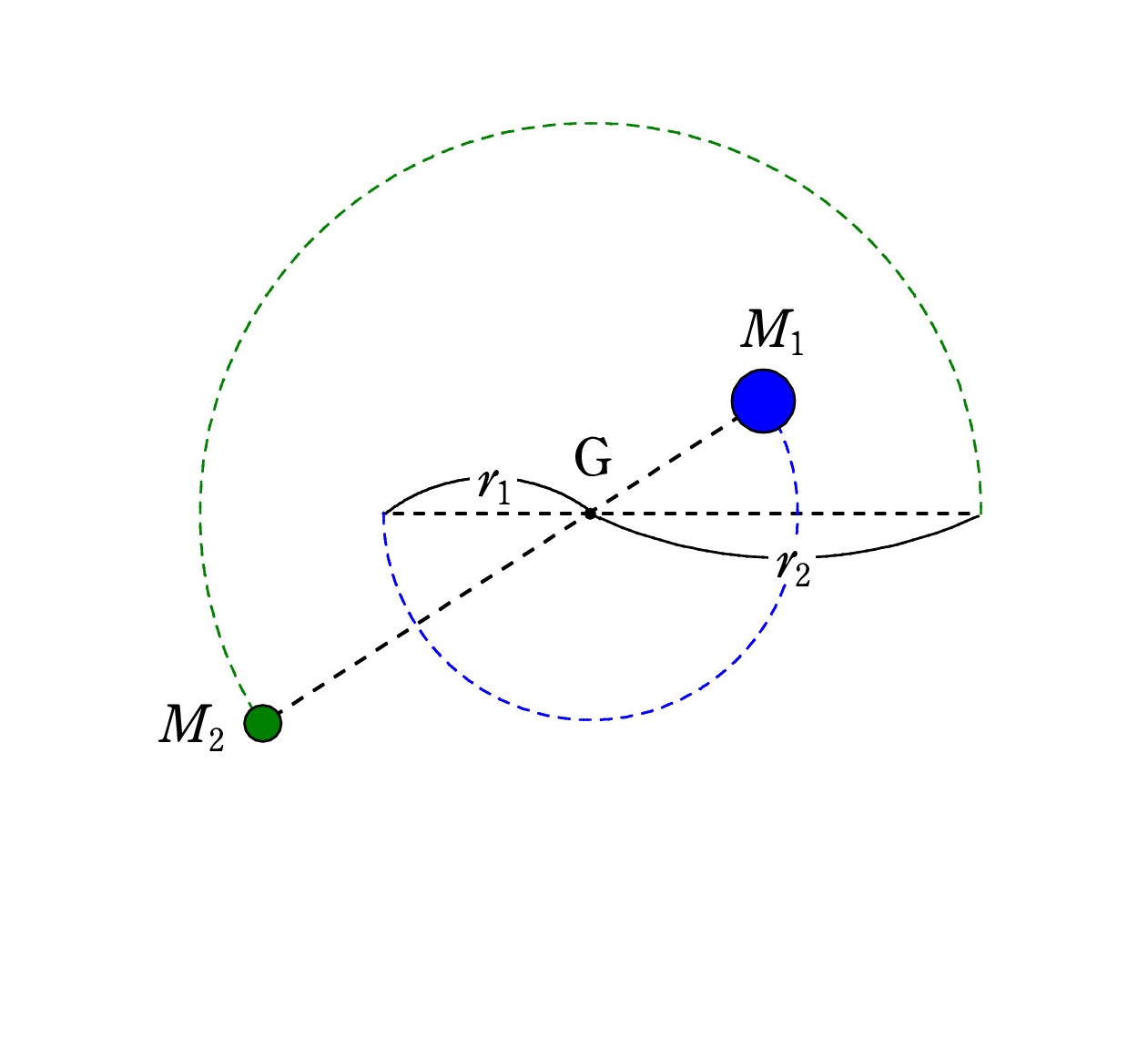
　星１の質量 Ｍ₁ は、星２の運動から求められる。　星２の円運動について、
　　　　　Ｍ₂ｖ₂² / r₂ ＝ ＧＭ₁Ｍ₂ / (r₁＋r₂)²　　そして、　Ｔ＝２π r₂ / v₂
　以上より、v₂ を消去して、Ｍ₁ を求めると、　　　Ｍ₁＝４π²r₂(r₁＋r₂)² /ＧＴ²
　同様に、星１の円運動から、　　　　Ｍ₂＝４π²r₁(r₁＋r₂)² /ＧＴ²
　Ｍ₁ の答えを見て、　r₁ と r₂ を入れ替えてもよい。　どちらの星を「星１」と呼んでもよいからである。　広い意味での 対称性 であり、答えのチェックとしても役立つ。

　なお、２つの答えより、　Ｍ₁ /Ｍ₂ ＝ r₂ /r₁　　これは回転中心Ｇが重心であることを示している。　２つの質点の重心は 質点間を質量の逆比に分ける点。
　ただ、つり合い式（あるいは運動方程式）の段階で、左辺を ｍｒω² の形にしておけば、　Ｍ₁ r₁ ω²＝Ｆ　と　Ｍ₂ r₂ ω²＝Ｆ　とから、Ｍ₁ /Ｍ₂ ＝ r₂ /r₁ は簡単に確認できる。
（ 角速度 ω＝２π/Ｔ は共通量 ）
　２つの星からなる 物体系には外力が働いていないので、重心は静止できる（一般には等速直線運動)。（エッセンス(上)ｐ66 (新版 p 67)）


　周期Ｔと ２つの星の間の距離 a(＝r₁＋r₂) までしか観測できない場合もある。
　それでも、　　Ｍ₁＋Ｍ₂ ＝(r₂＋r₁)・４π²(r₁＋r₂)² /ＧＴ²＝４π²a³ /ＧＴ²　のように、質量の和 Ｍ₁＋Ｍ₂ は分かる。
　これも、　Ｍ₁ r₁ ω²＝ ＧＭ₁Ｍ₂ / a²　と　Ｍ₂ r₂ ω²＝ ＧＭ₁Ｍ₂ / a²　とから、
　r₁＝…、　r₂＝…　として、　r₁ ＋ r₂　を a に置き換えると早く導ける。

　Ｍ₁＋Ｍ₂ を一定にしたとき（２つの星を確定したとき）、 a に応じて Ｔが変わる。
　Ｔ²/ a³ ＝ 一定　となるが、これは 連星系での ケプラーの第３法則 である。



　光のドップラー効果から、星の速さが分かり、質量が決定できることも多い。
　「森」の原子分野の問題 59 では そのような例を扱っている。














※X6※【 フーコーの振り子の解答 】


　北半球では時計回りに回転する。　南半球では反時計回りに回転する。

　地球は西から東へと自転している（そのため、太陽は東から上り西に沈む)。北極の上から見下ろすと、反時計回りに自転している。　振り子の振動面は 宇宙空間に対して不変なので、地球に対しては時計回りに回転していくように見える。
　南極の上から見下ろせば、地球の自転は時計回りになる。　そのため、振り子の振動面は 反時計回りに回転していくように見える。
　実は、極以外で考えるのは至難の業である。　問題文が「北半球では…」となっていることから、北半球では共通の回転方向であることを読み取り、北極で考えればよいことに気付きたい。

　フーコーがパリで公開実験した19世紀、地球の自転を疑う人はいなかったが、振動面が回転するのを目の当たりにして、自転が実感できたということである。
　振動を持続させるためには、振り子を長くし、おもりを重くするとよい。　フーコーは 67ｍ の針金に 28ｋg のおもりを吊るしたとのこと。
　極では１日に１回転だが、緯度が下がるにつれて回転時間が長くなり、赤道上では回転しなくなる。
















※Y1※【 柱体の振動周期の解答 】

図１：　Ｐを下に距離ｘずらすと、弾性力がｋｘ増し、浮力が ρ(Ｓｘ)ｇ 増す。
　　いずれも上向きの復元力だから、合力は和となり、（ｋ＋ρＳｇ）x
　　よって、Ｋ＝ｋ＋ρＳｇ の単振動であり、　Ｔ₁ ＝ 2π √ ｍ /(ｋ＋ρＳｇ)
　　　　　　　　　　　　　　　　　　　　　　　　　　（√ 以後の量は平方根の中、以下同様）

図２：　下にｘずらすと、密度 ρ₁ の液体による浮力が ρ₁(Ｓｘ)ｇ 増す。
　　一方、ρ₂ の液体による浮力は ρ₂(Ｓｘ)ｇ 減るので、復元力は差となり、
　　　　　　　ρ₁(Ｓｘ)ｇ−ρ₂(Ｓｘ)ｇ ＝ (ρ₁−ρ₂)Ｓｇｘ
　　よって、Ｋ＝(ρ₁−ρ₂)Ｓｇ の単振動であり、　Ｔ₂ ＝ 2π √ ｍ /{(ρ₁−ρ₂)Ｓｇ｝

　　 ρ₁＞ρ₂　つまり　下の密度＞上の密度 が必要な理由については 浮力の項を参照（★）


図３：　今までの考察により、下にｘずらすと、復元力は ｋｘ＋(ρ₁−ρ₂)Ｓｇｘ となる。
　　したがって、　Ｔ₃ ＝ 2π √ ｍ /{ｋ＋(ρ₁−ρ₂)Ｓｇ｝



　できた人は、さらに次の課題を考えてみてください。

【課題】
図１と図３において、ばねが上側ではなく、下側についていると（Ｐと容器の底を結ぶばねだと）、Ｔ₁ と Ｔ₃ はどのようになるか。

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　解答（※Y2※）は最後に
















※�W※【小球 P の運動の解答】

　静電気力による位置エネルギー U ＝ ｑV （ｑ と V は符号付き）を用いて、エネルギー保存則で考える。

問１　U ＝ ｑV より電位 V のグラフは 位置エネルギー U のグラフと見てよい（縦にｑ倍しただけ）。そして、位置エネルギーのグラフは、力学における滑らかな曲面の断面図と思ってよい。　曲面上で運動する P が A（位置エネルギー０の位置）から左に向かうとき、曲面の山を乗り越えないと点電荷に出会えない。 山の頂点は ｘ ＝ ｘ₀ にある。
　まず、ｘ₀ での電位 V_max は、　　V_max ＝ ｋ・2Q / ｘ₀ ＋ ｋ(−Q) /（ｘ₀−a）
　　ｘ₀ ＝ (2＋√2)a　を代入して整理すれば、
　　　　　V_max ＝ (√2−１)ｋQ / (√2＋１)a ＝（√２−１)² kQ / a　
　初めの運動エネルギー mv₀²/２ が位置エネルギーの最大値 ｑV_max より大きければ、山を越えて進める。
　したがって、　　　　ｖ₀ ＞ √(２ｑV_max / m) ＝ (２−√２)√(kqQ / ma)

　計算手順によって数値部分は見かけが異なる。うまく変形できなければ、２−√２ ＝ 0.585… になるか、電卓で確かめる手もある。


問２　負電荷 −q の場合は　U ＝（−ｑ) V ＝ −ｑV　であり、V のグラフを ＋− 反転させて考えればよい。ｘ₀ は谷になる。
　位置 A で放された P は左に動き始め、速さを増していく。ｘ₀ で最大の速さになった後、減速し、 A と同じ位置エネルギー ０ となる ｘ₂ で一瞬静止する。　次に右に運動するが、同じ位置での速さは左へ通過した時と同じであり、やがて A に戻る。行きと戻りの時間は等しい。　そして、この往復運動を繰り返す。
　行きと戻りの時間が等しいのは、微小区間に分割したとき、各区間ごとの時間が等しいことによる（速さが等しいから）。
　 負電荷 −q の場合の 速さの最大値 v_max について：　位置 A に比べ ｘ₀ での位置エネルギーは ｑV_max 低いので、 ｑV_max ＝ mv_max²/２ 　　 v_max は問１の答えと同じになる。
　
　初め、P をｘ₀ の位置で静かに放せば、静止し続ける。ただし、正電荷の場合は不安定で、わずかにずらせば、動き出してしまう。 負電荷なら安定で、ずらしても元に戻る（行き過ぎて振動する）。 すべて電位 V グラフから読み取れる。














※�X※【殻状導体の電荷分布の解答】

　 　外面にだけ分布する。

　＋の場合で説明する。　内面全体に＋があると、まさに電気力線の向かう先がない。　よって、内面全部が＋はありえない。
　内面の一部が−に帯電していれば、そこに向かうことはできる。　＋から出た電気力線に沿って電位が下がり−に達する。　電気力線は高電位側から低電位側に向かう。　ところが、＋も−も導体の内面にあって、等電位のはずで、これも矛盾を引き起こす。
　結局、内面には電荷がないことになり、外面にだけ分布していることになる。

　そして、殻の内部空間には電気力線がなく、電場がない。　殻の外部で電荷配置が変われば、殻の外面の電荷分布はそれに応じて変わるが、内部空間には影響が及ばない。　静電遮蔽 の状況である。














※�Y※【 Q₀ を取り巻く多重の殻状導体における電荷分布の解答】

　殻 i の内面は　−( Q₀ ＋Q₁＋ … ＋ Q _i-1 ）、　外面は 　Q₀ ＋ Q₁ ＋ … ＋ Q _i

　黄身を取り巻く殻１の内面に− Q₀ 、殻１の電荷保存から殻１の外面には　Q₀ ＋ Q₁ 、すると、殻２の内面に　−( Q₀ ＋ Q₁）、外面に　Q₀ ＋ Q₁ ＋ Q₂ 、・・・以下、同様。

　殻と殻の間では（電気力線が閉じ）等量の正負の電荷が向かい合うこと、ある殻の外面にはその殻の電荷に加えて内側の総電荷が顔を出すことに注意。　したがって、一番外の殻から内側に向かって解くこともできる。　さらには、ダイレクトに上記の答えを書くこともできる。
　殻の厚みや殻の間隔は電荷配置に影響しないことにも注意したい。　さらには、殻の形状も影響しない。

　振り返れば、質問 Q10 や Q13 の問題２のような具体例から理解し始め、慣れて特徴をつかみ、多重殻という一般解にたどり着いている。　一般的で 一見厳めしい問題に対しては、まず、シンプルな具体例で考え始めるのが鉄則 といえよう。　問題の作成者自身がそうしてたどり着いていることが多いのである。














※�Z※【アースに関する問題の解答】

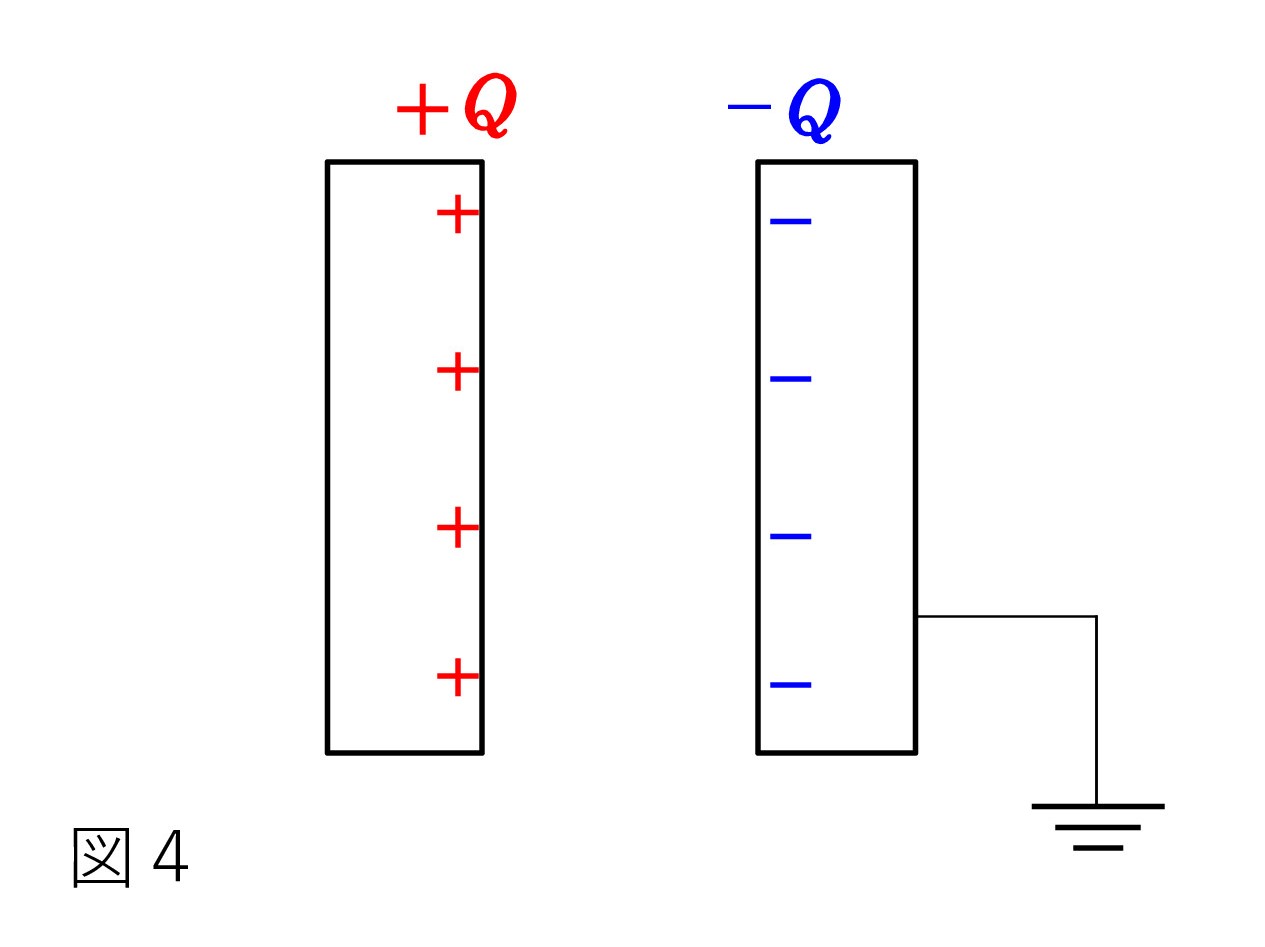（１）図３では、左端と右端の −Q/２ が反発し合っていて、互いに最も離れている。　右側をアースすると、右端にいた −Q/２ が地面に逃げる。　すると、左端の −Q/２ が自由になり、＋と中和する。　その結果、図４のようになる。　右側のアースで、左端の電荷まで０にできていることに注目。
　これで完全なコンデンサーとなる。　考え方はこの一通りではないが、金属内の電場が０であることと、孤立部分の電気量保存（電荷保存）により左極板の電荷が ＋Q であることは動かせない。
　なお、電気容量を C とすると、アースにつながる右側の電位は ０、左側の電位は
　 ＋Q / C である。

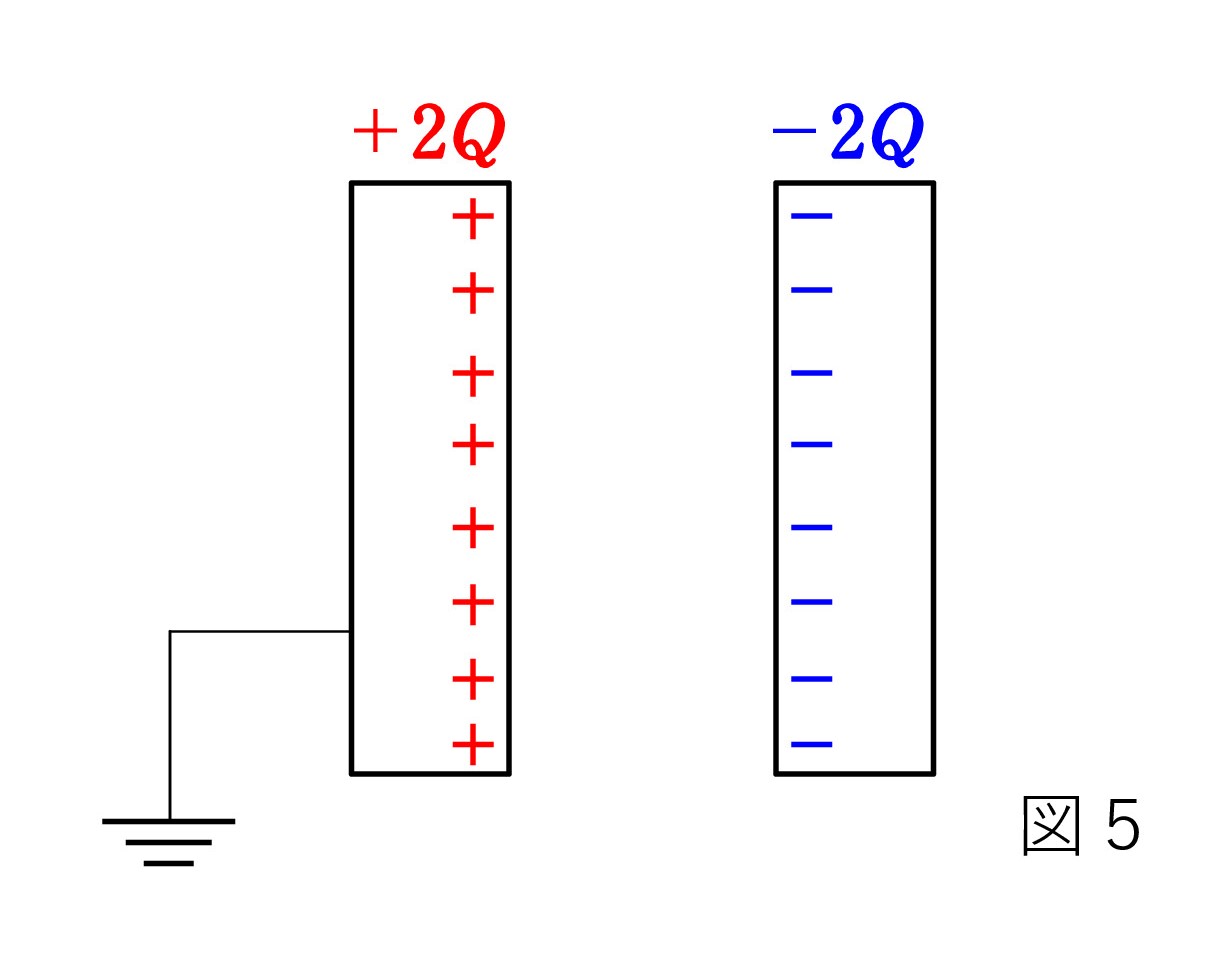（２）右側が孤立しているので、電荷は−2Q と定まる。　向かい合う左極板には、
　図５のように、＋2Q が現れる。　これは 静電誘導 であり、左側が初め持っていた電荷には無関係であることにも注意してほしい（図４では右側の初めの電荷が無関係）。
　　左側の電位は ０、右側の電位は −2Q / C となる。

（３）孤立部分はなく、両側の極板から電荷はなくなる。
　　２つの極板の電位は０で等しく、 電位差 V ＝ ０ より　Q ＝ C V ＝ ０ と考えてもよい。
　　地面は「導線」に置き換えてよく、２枚の極板をショートしたことになっている。
　　ただし、アースせず、２枚の極板を導線でつなぐだけの単なるショートだと、 内側の電荷はなくせても、 外側の −Q/２ はそれぞれ残ってしまう。

　このように、アースの役割はなかなかに奥深いが、入試問題では、アースは電位の基準点を決めるだけのものと思ってよい。　せいぜい、２箇所でアースがとられると、その間を「導線」でつないで考えるケースまでである（直流回路だと、電流が地面を通って流れ続ける可能性がある）。













※Y2※【 ばねが下側のときの 振動周期 Ｔ₁ と Ｔ₃ の解答 】

　つり合い位置でばねが自然長より縮んでいる（ケースＡ）か、伸びている（ケースＢ）かで弾性力の向きが異なる。Ｐが重い場合がＡ、軽い場合がＢに当たる。Ｐを下に距離ｘずらす場合で考える。

図１：
　Ａ……上向きの弾性力がｋｘ増し、浮力が ρ(Ｓｘ)ｇ 増すので、Ｔ₁ は変わらない。
　Ｂ……下向きの弾性力がｋｘ減る。これは上向きの力がｋｘ増すことと同等である。
　　　　浮力も増すので Ｔ₁ は変わらない。
　結局、ＡかＢかによらず、Ｔ₁ は変わらない。

図３：
　同様にして、弾性力の効果はばねが上側にあるか、下側にあるかにはよらない。
　そして、浮力の効果は 図２と同じだから、Ｔ₃ も変わらない。


　実は、ばねがＰを吊るしている図１や図３でも、ばねが自然長より縮んでいる可能性はあった。　Ｐが軽く、浮力で浮き上がるのを、ばねで下に押し付けているケースである。
　さらには、ｘずらす間にばねが伸びから縮みに変わったり、その逆が起こったりまで検討すれば完全になるが、頭が痛い。
　やはり、簡便さを重視するアンバランス法としては、「分かりやすいと思うケースで考えていく」に留めるのがよいだろう。

　せっかく色々な場合を考えたので、ばねの弾性力については 次のことを定理としておきたい。
　物体に取り付けられたばねは、物体がさらにｘ移動すると、 kx の復元力を生み出す。
　はじめ、ばねが 伸びているか 縮んでいるかに関係なく、移動する向きにも関係しない。
　この認識があれば、ばねで物体を吊るしているか、下から支えているかの差異はないと即断できる。

　














　　






















【質問について】　メールでの質問は次のアドレスまで。　　　　hiroba@mb.ccnw.ne.jp

　　　　　　　　　手紙またはFAXでの質問は河合出版を通してください。電話は、正確に伝わらないことが
　　　　　　　　　ありますので、できるだけ避けてください。



トップページに戻る